浅析java 循序与二元搜索算法
循序搜索法
就是一个一个去比较,找到时返回;
二元搜索法
二元搜索算法是在排好序的数组中找到特定的元素.
首先, 比较数组中间的元素,如果相同,则返回此元素的指针,表示找到了. 如果不相同, 此函数就会继续搜索其中大小相符的一半,然后继续下去. 如果剩下的数组长度为0,
则表示找不到,那么函数就会结束.
实现代码:
package com.zc.manythread;
import java.util.Random;
import java.util.Scanner;
/**
*
* @author 偶my耶
* 循环查找
* 二元查找
*/
public class LinearSearch {
//循序搜索
public static int LinearSearch(int[] list,int item)
{
for(int i = 0 ; i < list.length;i++)
{
if(list[i]==item)
return i;//找到传回的位置
}
return -1;//找不到时
}
//二元搜寻,传入的数先排序好,由小至大
public static int BinarySearch(int[] list,int item)
{
//初始左右二边
int left = 0 ;
int right = list.length;
//左边的索引位置小于右边的索引的位置
while(left<=right)
{
int mid = (left + right)/2;
if(list[mid]==item)
return mid;
else
{
//所查询值比中间值小,故值会在中间的左边数列
if(list[mid]>item)
{
right = mid -1;
}else
{
left = mid +1;
}
}
}
return -1;//找不到时
}
/**
* 产生随机数组
* @param count
* @return
*/
private static int[] createDate(int count) {
int[] data=new int[count];
Random rand = new Random();
boolean[] bool = new boolean[100];
int num = 0;
for (int i = 0; i < count; i++) {
do {
// 如果产生的数相同继续循环
num = rand.nextInt(100);
} while (bool[num]);
bool[num] = true;
data[i]=num;
}
return data;
}
public static void main(String args[])
{
//输入要查找的数
Scanner in = new Scanner(System.in);
//循序搜寻案列
int[] list = createDate(10);
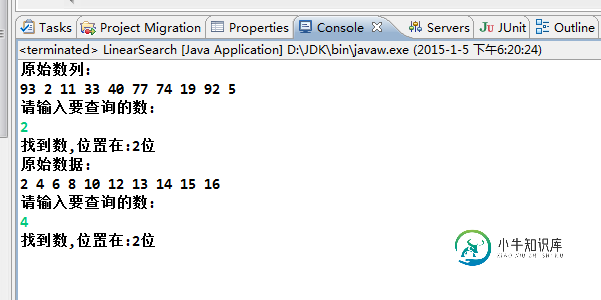
System.out.println("原始数列:");
for(int i = 0 ; i <list.length ; i ++)
{
System.out.print(list[i]+" ");
}
System.out.println("\r\n请输入要查询的数:");
int searchkey = in.nextInt();
int ans = LinearSearch(list,searchkey);
if(ans>-1)
{
System.out.println("找到数,位置在:"+(ans+1)+"位");
}
else
System.out.println("找不着");
//二元搜寻案列
int[] list2 = {2,4,6,8,10,12,13,14,15,16};
System.out.println("原始数据:");
for(int i = 0 ; i<list2.length ; i ++)
{
System.out.print(list2[i]+" ");
}
System.out.println("\r\n请输入要查询的数:");
int searchkey2 = in.nextInt();
int ans2 = BinarySearch(list2,searchkey2);
if(ans2>-1)
{
System.out.println("找到数,位置在:"+ans2+"位");
}
else
System.out.println("找不着!");
}
}
运行结果
以上就是本文的全部内容了,希望大家能够喜欢。
-
本文向大家介绍浅析java 归并排序算法,包括了浅析java 归并排序算法的使用技巧和注意事项,需要的朋友参考一下 归并排序(Merge)是将两个(或两个以上)有序表合并成一个新的有序表,即把待排序序列分为若干个子序列,每个子序列是有序的。然后再把有序子序列合并为整体有序序列。 归并排序是建立在归并操作上的一种有效的排序算法。该算法是采用分治法(Divide and Conquer)的一个非常典型
-
我说得对吗?
-
下面是一个迭代算法,可以在不使用堆栈的情况下按顺序遍历二进制搜索树(首先是,然后是,最后是): (想法:整个想法是找到树最左边的子节点,每次都找到手边节点的后续节点,并打印其值,直到不再剩下节点。) 有人声称,假设BST中有n个节点,该算法的时间复杂度为θ(n),这肯定是正确的。然而,我无法说服自己,因为我猜一些节点的遍历次数超过了常数,这取决于它们的子树中的节点数量,并且总结所有这些访问次数不会
-
树是一种非线性的数据结构,以分层的方式存储数据,它对于存储需要快速查找的数据非常有用。 树是一种一对多的数据结构。树又有很多子集,比如:二叉树、二叉搜索树、2-3树、红黑树等等。 现实例子就是公司的组织架构,总裁为树的最顶端叫根节点,各部门按照领导人区分为子树。 在计算机科学中,HTML结构就是典型的树结构 树的节点可以有0个或多个子节点。当一棵树(的所有节点)最多只能有两个子节点时,这样的树被称
-
代码是一个简单的二分搜索程序。我试着追踪程序,但它只会让我更加困惑。我不明白为什么嵌套的if has data,min,midpoint-1,&target和底部的else if语句has data,midpoint+1,max,target。
-
我有一个二进制搜索树,它的每个节点都有两个值。 所以它的节点是这样的。 我已经根据节点的“name”变量的升序在BST中插入了值。所以树的顺序遍历将按“name”的升序返回节点。 现在我想根据“值”变量的升序显示树节点。无需更改原始树。哪种算法/方法对此最有效?

