C++实现图的邻接矩阵表示

令狐钧

2023-03-14

本文向大家介绍C++实现图的邻接矩阵表示，包括了C++实现图的邻接矩阵表示的使用技巧和注意事项，需要的朋友参考一下

本文实例为大家分享了C++实现图的邻接矩阵表示代码，供大家参考，具体内容如下

1.遇到的问题：教材中写着子类Graphmtx(我用GrapMatrix)继承基类Graph

但是我在子类GraphMatrix中使用父类Graph的保护成员属性：maxVertices 显示没有声明（如下图）。

原来，c++中声明一个模板类及子类，在子类中如果需要访问父类的protected变量，需要使用父类的类作用域限定符，否则会报“identifier not found”错误。如果不是模板类，可以直接访问。

例如：要如下这样使用父类的保护成员属性，太麻烦了。

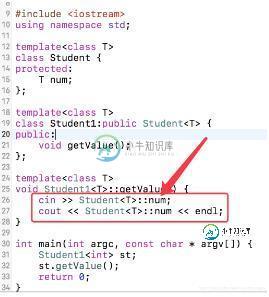
所以，我就不用继承基类的方法了。直接把Graph父类的保护成员属性放到GrapMatrix类中。

2.实现程序：

（1）GraphMatrix.h

#ifndef GraphMatrix_h
#define GraphMatrix_h
#include <iostream>
using namespace std;
 
const int DefaultVertices = 30; // 默认最大顶点数
 
template <class T, class E>
class GraphMatrix {
public:
 const E maxWeight = 100000; // 代表无穷大的值（=∞）
 GraphMatrix(int sz=DefaultVertices); // 构造函数
 ~GraphMatrix(); // 析构函数
 void inputGraph(); // 创建基于邻接矩阵的图
 void outputGraph(); // 输出图的所有顶点和边信息
 T getValue(int i); // 取顶点i的值，i不合理返回0
 E getWeight(int v1, int v2); // 取边(v1, v2)上的权值
 int getFirstNeighbor(int v); // 取顶点v的第一个邻接顶点
 int getNextNeighbor(int v, int w); // 取v的邻接顶点w的下一个邻接顶点
 bool insertVertex(const T& vertex); // 插入顶点vertice
 bool insertEdge(int v1, int v2, E cost); // 插入边(v1, v2)权值为cost
 bool removeVertex(int v); // 删去顶点v和所有与它相关联的边
 bool removeEdge(int v1, int v2); // 在图中删去边(v1, v2)
 int getVertexPos(T vertex); // 给出顶点vertice在图中的位置
private:
 int maxVertices; // 图中最大的顶点数
 int numEdges; // 当前边数
 int numVertices; // 当前顶点数
 T *VerticesList; // 顶点表
 E **Edge; // 邻接矩阵
};
 
// 构造函数
template <class T, class E>
GraphMatrix<T, E>::GraphMatrix(int sz) {
 int i, j;
 
 maxVertices = sz;
 numVertices = 0;
 numEdges = 0;
 VerticesList = new T[maxVertices]; // 创建顶点表数组
 Edge = new E*[maxVertices]; // 创建邻接矩阵数组
 for(i = 0; i < maxVertices; i++)
  Edge[i] = new E[maxVertices];
 for(i = 0; i < maxVertices; i++) { // 邻接矩阵初始化
  for(j = 0; j < maxVertices; j++)
  {
   if(i == j) // 矩阵对角处，即为同一顶点
    Edge[i][j] = 0;
   else // 不是同一顶点的，即两顶点一开始没有边相连，为无穷大∞
    Edge[i][j] = maxWeight;
  }
 }
}
 
// 析构函数
template <class T, class E>
GraphMatrix<T, E>::~GraphMatrix() {
 delete []VerticesList; // 释放动态分配的空间
 delete []Edge;
}
 
// 创建基于邻接矩阵的图
template <class T, class E>
void GraphMatrix<T, E>::inputGraph() {
 int i, j, k;
 int n, m; // 要输入的顶点数和边数
 T e1, e2; // 边的两端顶点
 E weight; // 边对应的权值
 
 cout << "请输入顶点数和边数:" << endl;
 cin >> n >> m;
 cout << "请输入顶点：" << endl;
 for(i = 0; i < n; i++) { // 建立顶点表数据
  cin >> e1;
  insertVertex(e1); // 插入
 }
 cout << "请输入边的两端顶点和权值:" << endl;
 i = 0;
 while(i < m){ // 输入边
  cin >> e1 >> e2 >> weight; // 输入端点信息
  j = getVertexPos(e1); // 查顶点号
  k = getVertexPos(e2);
  if(j == -1 || k == -1)
   cout << "边两端点信息有误，重新输入!" << endl;
  else {
   insertEdge(j, k, weight);
   i++;
  }
 } // for结束
}
 
// 输出图的所有顶点和边信息
template <class T, class E>
void GraphMatrix<T, E>::outputGraph() {
 int i, j, n, m;
 T e1, e2;
 E w;
 
 n = numVertices;
 m = numEdges;
 cout << "顶点数为：" << n << "，边数为：" << m << endl;
 for(i = 0; i < n; i++) {
  for(j = i+1; j < n; j++) {
   w = getWeight(i, j); // 取边上权值
   if(w > 0 && w < maxWeight) { // 有效，即这两顶点存在边
    e1 = getValue(i);
    e2 = getValue(j);
    cout << "(" << e1 << "," << e2 << "," << w << ")" << endl;
   }
  }
 } // for
}
 
// 给出顶点vertice在图中的位置
template <class T, class E>
int GraphMatrix<T, E>::getVertexPos(T vertex) {
 for(int i = 0; i < numVertices; i++)
  if(VerticesList[i] == vertex)
   return i;
 return -1;
}
 
// 取顶点i的值，i不合理返回NULL
template <class T, class E>
T GraphMatrix<T, E>::getValue(int i) {
 if(i >= 0 && i < numVertices)
  return VerticesList[i];
 return NULL;
}
 
// 取边(v1, v2)上的权值
template <class T, class E>
E GraphMatrix<T, E>::getWeight(int v1, int v2) {
 if(v1 != -1 && v2 != -1) // 存在这两个顶点
  return Edge[v1][v2];
 return 0;
}
 
// 取顶点v的第一个邻接顶点
template <class T, class E>
int GraphMatrix<T, E>::getFirstNeighbor(int v) {
 if(v != -1) {
  for(int col = 0; col < numVertices; col++)
   if(Edge[v][col] > 0 && Edge[v][col] <maxWeight)
    return col;
 }
 return -1;
}
 
// 取v的邻接顶点w的下一个邻接顶点
template <class T, class E>
int GraphMatrix<T, E>::getNextNeighbor(int v, int w) {
 if(v != -1 && w != -1) {
  for(int col = w+1; col < numVertices; col++) {
   if(Edge[v][col] > 0 && Edge[v][col] < maxWeight)
    return col;
  }
 }
 return -1;
}
 
// 插入顶点vertice
template <class T, class E>
bool GraphMatrix<T, E>::insertVertex(const T& vertex) {
 if(numVertices == maxVertices) // 顶点表满
  return false;
 VerticesList[numVertices++] = vertex;
 return true;
}
 
// 插入边(v1, v2)权值为cost
template <class T, class E>
bool GraphMatrix<T, E>::GraphMatrix<T, E>::insertEdge(int v1, int v2, E cost) {
 if(v1 > -1 && v1 < numVertices && v2 > -1 && v2 < numVertices && Edge[v1][v2] == maxWeight) { // 顶点v1,v2都存在，并且v1，v2没有边
  Edge[v1][v2] = Edge[v2][v1] = cost;
  numEdges++;
  return true;
 }
 return false;
}
 
// 删去顶点v和所有与它相关联的边
template <class T, class E>
bool GraphMatrix<T, E>::removeVertex(int v) {
 if(v < 0 && v > numVertices) // v不在图中，不删除
  return false;
 if(numVertices == 1) // 只剩一个顶点，不删除
  return false;
 int i, j;
 
 VerticesList[v] = VerticesList[numVertices-1]; // 用最后一个顶点替代当前要删的顶点
 // 删除与v相关联边数
 for(i = 0; i < numVertices; i++) {
  if(Edge[i][v] > 0 && Edge[i][v] < maxWeight)
   numEdges--;
 }
 // 用最后一列，填补第v列
 for(i = 0; i < numVertices; i++)
  Edge[i][v] = Edge[i][numVertices-1];
 numVertices--; // 顶点数减1
 // 用最后一行，填补第v行
 for(j = 0; j < numVertices; j++)
  Edge[v][j] = Edge[numVertices][j];
 return true;
}
 
// 在图中删去边(v1, v2)
template <class T, class E>
bool GraphMatrix<T, E>::removeEdge(int v1, int v2) {
 if(v1 > -1 && v1 < numVertices && v2 > -1 && v2 < numVertices && Edge[v1][v2] < maxWeight) {
  Edge[v1][v2] = Edge[v2][v1] = maxWeight;
  numEdges--; // 边数减1
  return true;
 }
 return false;
}
 
#endif /* GraphMatrix_h */

（2）main.cpp

// 测试数据：
/*
5 7
A B C D E
A B 24 A C 46 B C 15 B E 67 C B 37 C D 53 E D 31
 */
 
#include "GraphMatrix.h"
 
int main(int argc, const char * argv[]) {
 GraphMatrix<char, int> st; // 声明对象
 bool finished = false;
 int choice;
 char e1, e2, next;
 int weight;
 
 while(!finished) {
  cout << "[1]创建基于邻接矩阵的图" << endl;
  cout << "[2]输出图的所有顶点和边信息" << endl;
  cout << "[3]取顶点v的第一个邻接顶点" << endl;
  cout << "[4]取v的邻接顶点w的下一个邻接顶点" << endl;
  cout << "[5]插入顶点" << endl;
  cout << "[6]插入边" << endl;
  cout << "[7]删除顶点" << endl;
  cout << "[8]删除边" << endl;
  cout << "[9]退出" << endl;
  cout << "请输入选择[1-9]：";
  cin >> choice;
  switch(choice) {
   case 1:
    st.inputGraph();
    break;
   case 2:
    st.outputGraph();
    break;
   case 3:
    cout << "请输入顶点:";
    cin >> e1;
    e2 = st.getValue(st.getFirstNeighbor(st.getVertexPos(e1)));
    if(e2)
     cout << "顶点" << e1 << "的第一个邻接顶点为:" << e2 << endl;
    else
     cout << "顶点" << e1 << "没有邻接顶点！" << endl;
    break;
   case 4:
    cout << "请输入顶点v和邻接顶点w:";
    cin >> e1 >> e2;
    next = st.getValue(st.getNextNeighbor(st.getVertexPos(e1), st.getVertexPos(e2)));
    if(next)
     cout << "顶点" << e1 << "的邻接顶点" << e2 << "的下一个邻接顶点为:" << next << endl;
    else
     cout << "顶点" << e1 << "的邻接顶点" << e2 << "没有下一个邻接顶点！" << endl;
    break;
   case 5:
    cout << "请输入要插入的顶点：";
    cin >> e1;
    if(st.insertVertex(e1))
     cout << "插入成功！" << endl;
    else
     cout << "表已满，插入失败！" << endl;
    break;
   case 6:
    cout << "请输入要插入的边的信息:" << endl;
    cin >> e1 >> e2 >> weight;
    st.insertEdge(st.getVertexPos(e1), st.getVertexPos(e2), weight);
    break;
   case 7:
    cout << "请输入要删除的顶点：";
    cin >> e1;
    if(st.removeVertex(st.getVertexPos(e1)))
     cout << "顶点" << e1 << "已删除!" << endl;
    else
     cout << "顶点" << e1 << "不在图中!" << endl;
    break;
   case 8:
    cout << "请输入要删除的边的两个端点：" << endl;
    cin >> e1 >> e2;
    st.removeEdge(st.getVertexPos(e1), st.getVertexPos(e2));
    break;
   case 9:
    finished = true;
    break;
   default:
    cout << "选择输入错误，请重新输入!" << endl;
  }
 }
 return 0;
}

测试结果：

以上就是本文的全部内容，希望对大家的学习有所帮助，也希望大家多多支持小牛知识库。

C++实现图的邻接矩阵表示

相关阅读

相关文章

相关问答

相关工具

相关文档