JS实现的A*寻路算法详解
本文实例讲述了JS实现的A*寻路算法。分享给大家供大家参考,具体如下:
这两天在做百度前端技术学院的题目,其中有涉及到寻路相关的,于是就找来相关博客进行阅读。
看了Create Chen写的理解A*寻路算法具体过程之后,我很快就理解A*算法的原理。不得不说作者写的很好,通熟易懂,图片也做的很好,可见作者在这上面是花了心思的。如果让我写,我是写不来这么好的。
唯一的不足就是,因为我学的是js,因此最后给我的源码我是用不了的......因此才有自己写一篇的打算,方面学习js人的学习。然而前面的描述我就借用他的了,因为如果然我的表达能力实在是太渣了。
简易地图

如图所示简易地图, 其中绿色方块的是起点 (用 A 表示), 中间蓝色的是障碍物, 红色的方块 (用 B 表示) 是目的地. 为了可以用一个二维数组来表示地图, 我们将地图划分成一个个的小方块.
二维数组在游戏中的应用是很多的, 比如贪吃蛇和俄罗斯方块基本原理就是移动方块而已. 而大型游戏的地图, 则是将各种"地貌"铺在这样的小方块上.
寻路步骤
1. 从起点A开始, 把它作为待处理的方格存入一个"开启列表", 开启列表就是一个等待检查方格的列表.
2. 寻找起点A周围可以到达的方格, 将它们放入"开启列表", 并设置它们的"父方格"为A.
3. 从"开启列表"中删除起点 A, 并将起点 A 加入"关闭列表", "关闭列表"中存放的都是不需要再次检查的方格

图中浅绿色描边的方块表示已经加入 "开启列表" 等待检查. 淡蓝色描边的起点 A 表示已经放入 "关闭列表" , 它不需要再执行检查.
从 "开启列表" 中找出相对最靠谱的方块, 什么是最靠谱? 它们通过公式 F=G+H 来计算.
F = G + H
G 表示从起点 A 移动到网格上指定方格的移动耗费 (可沿斜方向移动).
H 表示从指定的方格移动到终点 B 的预计耗费 (H 有很多计算方法, 这里我们设定只可以上下左右移动).
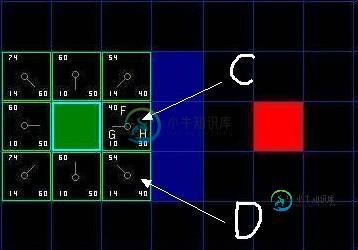
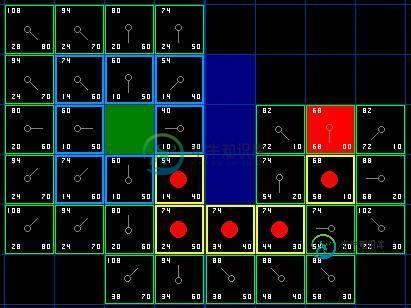
我们假设横向移动一个格子的耗费为10, 为了便于计算, 沿斜方向移动一个格子耗费是14. 为了更直观的展示如何运算 FGH, 图中方块的左上角数字表示 F, 左下角表示 G, 右下角表示 H. 看看是否跟你心里想的结果一样?
从 "开启列表" 中选择 F 值最低的方格 C (绿色起始方块 A 右边的方块), 然后对它进行如下处理:
4. 把它从 "开启列表" 中删除, 并放到 "关闭列表" 中.
5. 检查它所有相邻并且可以到达 (障碍物和 "关闭列表" 的方格都不考虑) 的方格. 如果这些方格还不在 "开启列表" 里的话, 将它们加入 "开启列表", 计算这些方格的 G, H 和 F 值各是多少, 并设置它们的 "父方格" 为 C.
6. 如果某个相邻方格 D 已经在 "开启列表" 里了, 检查如果用新的路径 (就是经过C 的路径) 到达它的话, G值是否会更低一些, 如果新的G值更低, 那就把它的 "父方格" 改为目前选中的方格 C, 然后重新计算它的 F 值和 G 值 (H 值不需要重新计算, 因为对于每个方块, H 值是不变的). 如果新的 G 值比较高, 就说明经过 C 再到达 D 不是一个明智的选择, 因为它需要更远的路, 这时我们什么也不做.
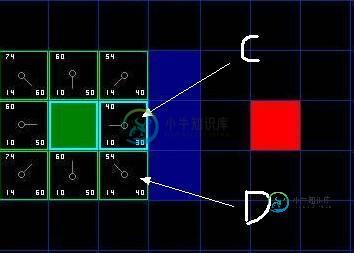
如图, 我们选中了 C 因为它的 F 值最小, 我们把它从 "开启列表" 中删除, 并把它加入 "关闭列表". 它右边上下三个都是墙, 所以不考虑它们. 它左边是起始方块, 已经加入到 "关闭列表" 了, 也不考虑. 所以它周围的候选方块就只剩下 4 个. 让我们来看看 C 下面的那个格子, 它目前的 G 是14, 如果通过 C 到达它的话, G将会是 10 + 10, 这比 14 要大, 因此我们什么也不做.
然后我们继续从 "开启列表" 中找出 F 值最小的, 但我们发现 C 上面的和下面的同时为 54, 这时怎么办呢? 这时随便取哪一个都行, 比如我们选择了 C 下面的那个方块 D.
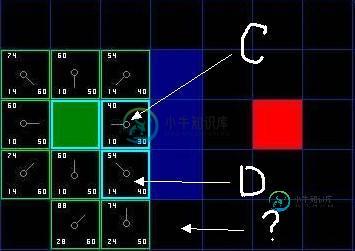
D 右边已经右上方的都是墙, 所以不考虑, 但为什么右下角的没有被加进 "开启列表" 呢? 因为如果 C 下面的那块也不可以走, 想要到达 C 右下角的方块就需要从 "方块的角" 走了, 在程序中设置是否允许这样走. (图中的示例不允许这样走)
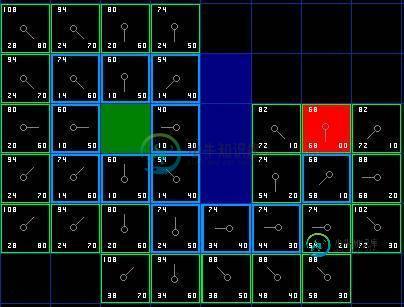
就这样, 我们从 "开启列表" 找出 F 值最小的, 将它从 "开启列表" 中移掉, 添加到 "关闭列表". 再继续找出它周围可以到达的方块, 如此循环下去...
那么什么时候停止呢? —— 当我们发现 "开始列表" 里出现了目标终点方块的时候, 说明路径已经被找到.
如何找回路径
如上图所示, 除了起始方块, 每一个曾经或者现在还在 "开启列表" 里的方块, 它都有一个 "父方块", 通过 "父方块" 可以索引到最初的 "起始方块", 这就是路径.
将整个过程抽象
把起始格添加到 "开启列表"
do
{
寻找开启列表中F值最低的格子, 我们称它为当前格.
把它切换到关闭列表.
对当前格相邻的8格中的每一个
if (它不可通过 || 已经在 "关闭列表" 中)
{
什么也不做.
}
if (它不在开启列表中)
{
把它添加进 "开启列表", 把当前格作为这一格的父节点, 计算这一格的 FGH
if (它已经在开启列表中)
{
if (用G值为参考检查新的路径是否更好, 更低的G值意味着更好的路径)
{
把这一格的父节点改成当前格, 并且重新计算这一格的 GF 值.
}
} while( 目标格已经在 "开启列表", 这时候路径被找到)
如果开启列表已经空了, 说明路径不存在.
最后从目标格开始, 沿着每一格的父节点移动直到回到起始格, 这就是路径.
js代码:
//其中的MAP.arr是二维数组
function searchRoad(start_x,start_y,end_x,end_y){
var openList=[], //开启列表
closeList=[], //关闭列表
result=[], //结果数组
result_index; //结果数组在开启列表中的序号
openList.push({x:start_x,y:start_y,G:0});//把当前点加入到开启列表中,并且G是0
do{
var currentPoint = openList.pop();
closeList.push(currentPoint);
var surroundPoint=SurroundPoint(currentPoint);
for(var i in surroundPoint) {
var item = surroundPoint[i]; //获得周围的八个点
if (
item.x>=0 && //判断是否在地图上
item.y>=0 &&
item.x<MAP.rows &&
item.y<MAP.cols &&
MAP.arr[item.x][item.y] != 1 && //判断是否是障碍物
!existList(item, closeList) && //判断是否在关闭列表中
MAP.arr[item.x][currentPoint.y]!=1 && //判断之间是否有障碍物,如果有障碍物是过不去的
MAP.arr[currentPoint.x][item.y]!=1) {
//g 到父节点的位置
//如果是上下左右位置的则g等于10,斜对角的就是14
var g = currentPoint.G + ((currentPoint.x - item.x) * (currentPoint.y - item.y) == 0 ? 10 : 14);
if (!existList(item, openList)) { //如果不在开启列表中
//计算H,通过水平和垂直距离进行确定
item['H'] = Math.abs(end_x - item.x) * 10 + Math.abs(end_y - item.y) * 10;
item['G'] = g;
item['F'] = item.H + item.G;
item['parent'] = currentPoint;
openList.push(item);
}
else { //存在在开启列表中,比较目前的g值和之前的g的大小
var index = existList(item, openList);
//如果当前点的g更小
if (g < openList[index].G) {
openList[index].parent = currentPoint;
openList[index].G = g;
openList[index].F=g+openList[index].H;
}
}
}
}
//如果开启列表空了,没有通路,结果为空
if(openList.length==0) {
break;
}
openList.sort(sortF);//这一步是为了循环回去的时候,找出 F 值最小的, 将它从 "开启列表" 中移掉
}while(!(result_index=existList({x:end_x,y:end_y},openList)));
//判断结果列表是否为空
if(!result_index) {
result=[];
}
else {
var currentObj=openList[result_index];
do{
//把路劲节点添加到result当中
result.unshift({
x:currentObj.x,
y:currentObj.y
});
currentObj=currentObj.parent;
}while (currentObj.x!=start_x || currentObj.y!=start_y);
}
return result;
}
//用F值对数组排序
function sortF(a,b){
return b.F- a.F;
}
//获取周围八个点的值
function SurroundPoint(curPoint){
var x=curPoint.x,y=curPoint.y;
return [
{x:x-1,y:y-1},
{x:x,y:y-1},
{x:x+1,y:y-1},
{x:x+1,y:y},
{x:x+1,y:y+1},
{x:x,y:y+1},
{x:x-1,y:y+1},
{x:x-1,y:y}
]
}
//判断点是否存在在列表中,是的话返回的是序列号
function existList(point,list) {
for(var i in list) {
if(point.x==list[i].x && point.y==list[i].y) {
return i;
}
}
return false;
}
更多关于JavaScript相关内容感兴趣的读者可查看本站专题:《JavaScript数学运算用法总结》、《JavaScript数据结构与算法技巧总结》、《JavaScript数组操作技巧总结》、《JavaScript排序算法总结》、《JavaScript遍历算法与技巧总结》、《JavaScript查找算法技巧总结》及《JavaScript错误与调试技巧总结》
希望本文所述对大家JavaScript程序设计有所帮助。
-
本文向大家介绍java实现dijkstra最短路径寻路算法,包括了java实现dijkstra最短路径寻路算法的使用技巧和注意事项,需要的朋友参考一下 【引用】迪杰斯特拉(Dijkstra)算法是典型最短路径算法,用于计算一个节点到其他节点的最短路径。 它的主要特点是以起始点为中心向外层层扩展(广度优先搜索思想),直到扩展到终点为止。 基本思想 通过Dijkstra计算图G中的最短路径时,需要指
-
主要内容:src/runoob/graph/Path.java 文件代码:图的寻路算法也可以通过深度优先遍历 dfs 实现,寻找图 graph 从起始 s 点到其他点的路径,在上一小节的实现类中添加全局变量 from数组记录路径,from[i] 表示查找的路径上i的上一个节点。 首先构造函数初始化寻路算法的初始条件,from = new int[G.V()] 和 from = new int[G.V()],并在循环中设置默认值,visited 数组全部为false,fr
-
实现的简单A*算法寻路Demo。A*寻路一般可用于游戏当中计算人物走动的线路。Demo测试方法是,迷宫中黑点是障碍物,绿点是可以走过的点,红点是起始点,然后点击任意绿点会生成一个灰色点,设置为终点。点击屏幕右上角的“移动按钮”,红点便开始了它的A*寻路之旅。 [Code4App.com]
-
本文向大家介绍js实现跨域的方法实例详解,包括了js实现跨域的方法实例详解的使用技巧和注意事项,需要的朋友参考一下 本文实例讲述了js实现跨域的方法。分享给大家供大家参考。具体分析如下: 由于同源策略的限制,XMLHttpRequest只允许请求当前源(包含域名、协议、端口)的资源。 json与jsonp的区别: JSON是一种数据交换格式,而JSONP是一种依靠开发人员创造出的一种非官方跨域数据
-
本文向大家介绍PHP树的深度编历生成迷宫及A*自动寻路算法实例分析,包括了PHP树的深度编历生成迷宫及A*自动寻路算法实例分析的使用技巧和注意事项,需要的朋友参考一下 本文实例讲述了PHP树的深度编历生成迷宫及A*自动寻路算法。分享给大家供大家参考。具体分析如下: 有一同事推荐了三思的迷宫算法,看了感觉还不错,就转成php 三思的迷宫算法是采用树的深度遍历原理,这样生成的迷宫相当的细,而且死胡同数
-
本文向大家介绍Js面试算法详解,包括了Js面试算法详解的使用技巧和注意事项,需要的朋友参考一下 素数 Q:你将如何验证一个素数? A:一个素数只能被它自己和1整除。所以,我将运行一个while循环并加1。(看代码示例,如果你无法理解,那这不是你的菜。先回去学习javaScript基础知识然后再回来吧。) 方法1 Q:你能做得更好吗? A:可以。除数一次增加1个。 在3之后我可以增加2.如果一个数可
-
本文向大家介绍JS 实现计算器详解及实例代码(一),包括了JS 实现计算器详解及实例代码(一)的使用技巧和注意事项,需要的朋友参考一下 Javascript 实现计算器: 系列文章: JS 实现计算器详解及实例代码(一) Javascript 实现计算器时间功能详解及实例(二) 小型JavaScript计算器 自己寻思出的解决方案,比较笨拙的方法,虽然完成了但是还有不少bug,用的方法也不是最有效
-
本文向大家介绍D3.js实现饼状图的方法详解,包括了D3.js实现饼状图的方法详解的使用技巧和注意事项,需要的朋友参考一下 前言 小编在之前已经跟大家分享过关于怎样用柱状图和折线图这两种基本图表。这两种图表都是有坐标轴的,现在来说一种没有坐标轴的图表——饼图。 饼状图实现 还是和之前一样,我们先把简单的画图框架搭起来,添加SVG画布。但是这里需要注意的是,为了方便后面画饼图上的弧形,我们把组合这些

