java简单实现八叉树图像处理代码示例

一晃工作有段时间了，第一次写博客，有点不知道怎么写，大家将就着看吧，说的有什么不正确的也请大家指正。

最近工作中用到了一个图像压缩的功能。找了一些工具，没有太好的选择。最后选了一个叫jdeli的，奈何效率又成了问题。我迫于无奈就只能研究了下它的源码，却发现自己对它的一个减色量化算法起了兴趣，可是尴尬的自己完全不明白它写的什么，就起了一个自己实现一个量化颜色算法的念头。

自己找了一些资料，找到三个比较常用的颜色处理算法：

流行色算法：

具体的算法就是，先对一个图像的所有颜色出现的次数进行统计，选举出出现次数最多的256个颜色作为图片的调色板的颜色，然后再次遍历图片的所有像素，对每个像素找出调色板中的最接近的颜色（这里我用的是方差的方式），写回到图片中。这个算法的实现比较简单，但是失真比较严重，图像中一些出现频率较低，但对人眼的视觉效挺明显的信息将丢失。比如，图像中存在的高亮度斑点，由于出现的次数少，很可能不能被算法选中，将被丢失。

中位切分算法：

这个算法我没有研究，想要了解的同学，可以看下这篇文章,里面有三种算法的介绍。

八叉树

这个算法就是我最后选用的算法，它的主要思想就是把图像的RGB颜色值转成二进制分布到八叉树中，例如：（173,234,144）

转成二进制就是（10101101,11101010,10010000），将R,G,B的第一位取出来组成（111），作为root节点的子节点，其中111作为root子节点数组的索引，以此类推，一直到最后一位，然后在叶子节点上存放这个颜色的分量值以及其出现的次数。具体看图。

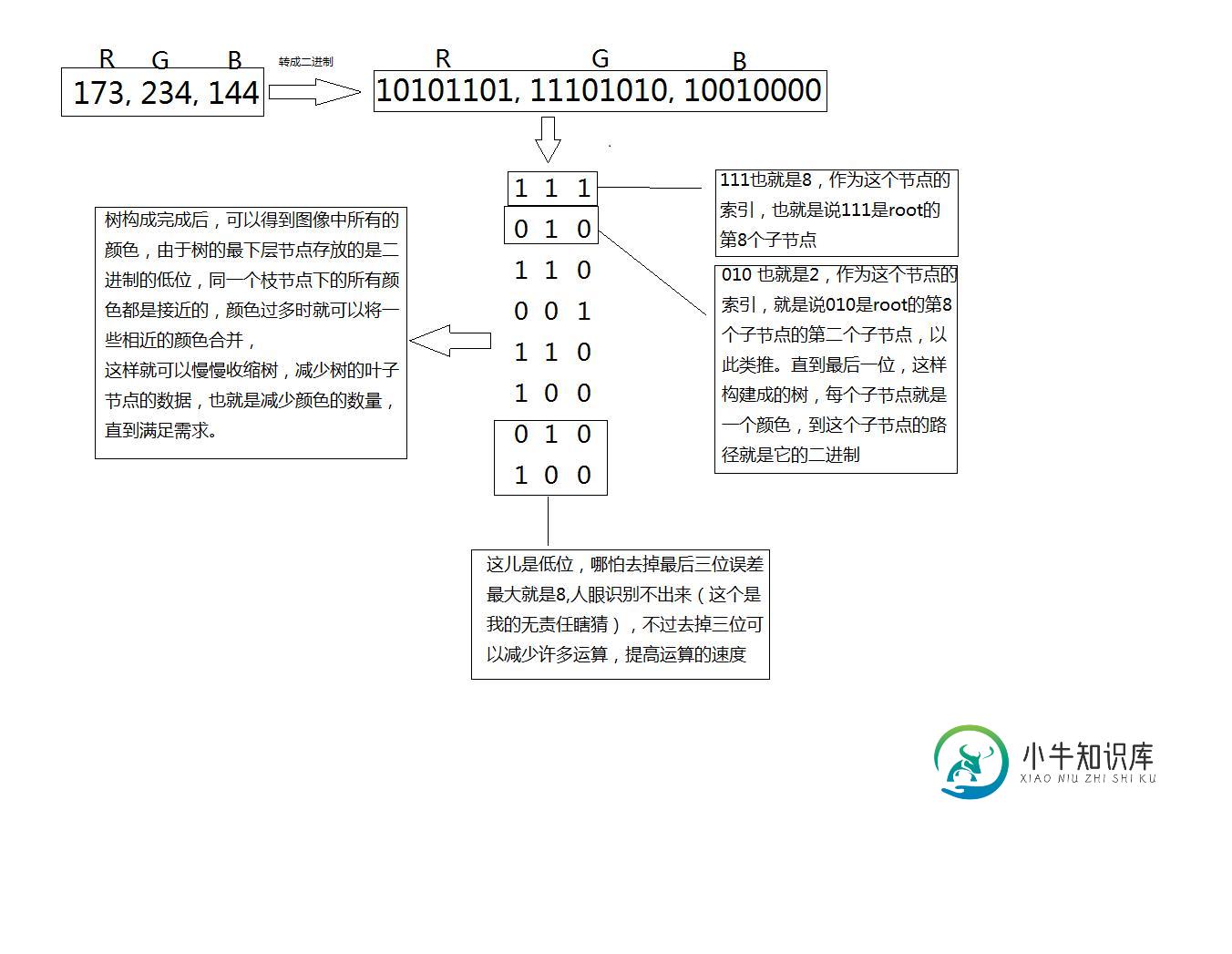
其中我比较疑惑的有一个处理就是叶子节点的合并策略，这儿我用的最笨的一个方法，就是找到层次最深的节点，然后合并，有点简单粗暴，有别的比较好的方法，也请大家给我留言。图片太大上传不了了，直接上代码了，代码没有重构，大家凑合看吧。

package com.gys.pngquant.octree;
import java.util.ArrayList;
import java.util.HashMap;
import java.util.List;
import java.util.Map;
/**
 * 
 *
 * @ClassName  类名：Node
 * @Description 功能说明： 
 * <p>
 *   八叉树实现
 * </p>
 * 
 *  2015-12-16  guoys 创建该类功能。
 *
 **********************************************************
 * </p>
 */
public class Node{
	private int depth = 0;
	// 为0时为root节点
	private Node parent;
	private Node[] children = new Node[8];
	private Boolean isLeaf = false;
	private int rNum = 0;
	private int gNum = 0;
	private int bNum = 0;
	private int piexls = 0;
	private Map<Integer, List<Node>> levelMapping;
	// 存放层次和node的关系
	public int getRGBValue(){
		int r = this.rNum / this.piexls;
		int g = this.gNum / this.piexls;
		int b = this.bNum / this.piexls;
		return (r << 16 | g << 8 | b);
	}
	public Map<Integer, List<Node>> getLevelMapping() {
		return levelMapping;
	}
	public void afterSetParam(){
		if(this.getParent() == null && this.depth == 0){
			levelMapping = new HashMap<Integer, List<Node>>();
			for (int i = 1; i <= 8; i++) {
				levelMapping.put(i, new ArrayList<Node>());
			}
		}
	}
	public int getrNum() {
		return rNum;
	}
	public void setrNum(int rNum) {
		if(!isLeaf){
			throw new UnsupportedOperationException();
		}
		this.rNum = rNum;
	}
	public int getgNum() {
		return gNum;
	}
	public void setgNum(int gNum) {
		if(!isLeaf){
			throw new UnsupportedOperationException();
		}
		this.gNum = gNum;
	}
	public int getbNum() {
		return bNum;
	}
	public void setbNum(int bNum) {
		if(!isLeaf){
			throw new UnsupportedOperationException();
		}
		this.bNum = bNum;
	}
	public int getPiexls() {
		return piexls;
	}
	public void setPiexls(int piexls) {
		if(!isLeaf){
			throw new UnsupportedOperationException();
		}
		this.piexls = piexls;
	}
	public int getDepth() {
		return depth;
	}
	// 返回节点原有的子节点数量
	public int mergerLeafNode(){
		if(this.isLeaf){
			return 1;
		}
		this.setLeaf(true);
		int rNum = 0;
		int gNum = 0;
		int bNum = 0;
		int pixel = 0;
		int i = 0;
		for (Node child : this.children) {
			if(child == null){
				continue;
			}
			rNum += child.getrNum();
			gNum += child.getgNum();
			bNum += child.getbNum();
			pixel += child.getPiexls();
			i += 1;
		}
		this.setrNum(rNum);
		this.setgNum(gNum);
		this.setbNum(bNum);
		this.setPiexls(pixel);
		this.children = null;
		return i;
	}
	// 获取最深层次的node
	public Node getDepestNode(){
		for (int i = 7; i > 0; i--) {
			List<Node> levelList = this.levelMapping.get(i);
			if(!levelList.isEmpty()){
				return levelList.remove(levelList.size() - 1);
			}
		}
		return null;
	}
	// 获取叶子节点的数量
	public int getLeafNum(){
		if(isLeaf){
			return 1;
		}
		int i = 0;
		for (Node child : this.children) {
			if(child != null){
				i += child.getLeafNum();
			}
		}
		return i;
	}
	public void setDepth(int depth) {
		this.depth = depth;
	}
	public Node getParent() {
		return parent;
	}
	public void setParent(Node parent) {
		this.parent = parent;
	}
	public Node[] getChildren() {
		return children;
	}
	public Node getChild(int index){
		return children[index];
	}
	public void setChild(int index, Node node){
		children[index] = node;
	}
	public Boolean isLeaf() {
		return isLeaf;
	}
	public void setPixel(int r, int g, int b){
		this.rNum += r;
		this.gNum += g;
		this.bNum += b;
		this.piexls += 1;
	}
	public void setLeaf(Boolean isLeaf) {
		this.isLeaf = isLeaf;
	}
	public void add8Bite2Root(int _taget, int _speed){
		if(depth != 0 || this.parent != null){
			throw new UnsupportedOperationException();
		}
		int speed = 7 + 1 - _speed;
		int r = _taget >> 16 & 0xFF;
		int g = _taget >> 8 & 0xFF;
		int b = _taget & 0xFF;
		Node proNode = this;
		for (int i=7;i>=speed;i--){
			int item = ((r >> i & 1) << 2) + ((g >> i & 1) << 1) + (b >> i & 1);
			Node child = proNode.getChild(item);
			if(child == null){
				child = new Node();
				child.setDepth(8-i);
				child.setParent(proNode);
				child.afterSetParam();
				this.levelMapping.get(child.getDepth()).add(child);
				proNode.setChild(item, child);
			}
			if(i == speed){
				child.setLeaf(true);
			}
			if(child.isLeaf()){
				child.setPixel(r, g, b);
				break;
			}
			proNode = child;
		}
	}
	public static Node build(int[][] matrix, int speed){
		Node root = new Node();
		root.afterSetParam();
		for (int[] row : matrix) {
			for (int cell : row) {
				root.add8Bite2Root(cell, speed);
			}
		}
		return root;
	}
	public static byte[] mergeColors(Node root, int maxColors){
		byte[] byteArray = new byte[maxColors * 3];
		List<byte> result = new ArrayList<byte>();
		int leafNum = root.getLeafNum();
		try{
			while(leafNum > maxColors){
				int mergerLeafNode = root.getDepestNode().mergerLeafNode();
				leafNum -= (mergerLeafNode - 1);
			}
		}
		catch(Exception e){
			e.printStackTrace();
		}
		fillArray(root, result, 0);
		int i = 0;
		for (byte byte1 : result) {
			byteArray[i++] = byte1;
		}
		return byteArray;
	}
	private static void fillArray(Node node, List<byte> result, int offset){
		if(node == null){
			return;
		}
		if(node.isLeaf()){
			result.add((byte) (node.getrNum() / node.getPiexls()));
			result.add((byte) (node.getgNum() / node.getPiexls()));
			result.add((byte) (node.getbNum() / node.getPiexls()));
		} else{
			for (Node child : node.getChildren()) {
				fillArray(child, result, offset);
			}
		}
	}
}

可怜我大学唯二挂的数据结构。代码实现的只是八叉树，对一个1920*1080图片量化，耗时大概是450ms，如果层次-2的话大概是100ms左右。

好吧，这篇就这样吧，本来写之前，感觉自己想说的挺多的，结果写的时候就不知道怎么说了，大家见谅。

总结

以上就是本文关于java简单实现八叉树图像处理代码示例的全部内容，希望对大家有所帮助。感兴趣的朋友可以继续参阅本站其他相关专题，如有不足之处，欢迎留言指出。感谢朋友们对本站的支持！