对Pytorch神经网络初始化kaiming分布详解

函数的增益值

torch.nn.init.calculate_gain(nonlinearity, param=None)

提供了对非线性函数增益值的计算。

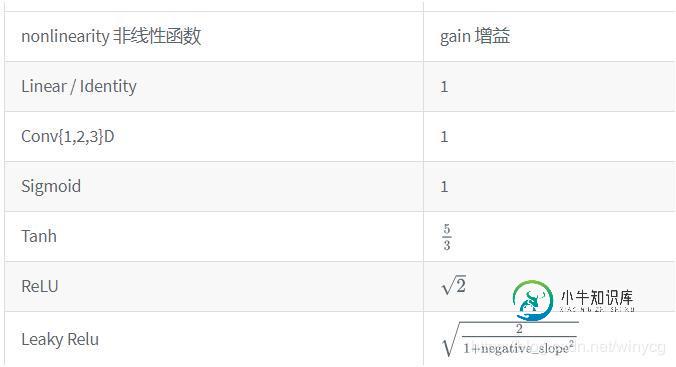
增益值gain是一个比例值，来调控输入数量级和输出数量级之间的关系。

fan_in和fan_out

pytorch计算fan_in和fan_out的源码


def _calculate_fan_in_and_fan_out(tensor):
 dimensions = tensor.ndimension()
 if dimensions < 2:
  raise ValueError("Fan in and fan out can not be computed 
  for tensor with fewer than 2 dimensions")

 if dimensions == 2: # Linear
  fan_in = tensor.size(1)
  fan_out = tensor.size(0)
 else:
  num_input_fmaps = tensor.size(1)
  num_output_fmaps = tensor.size(0)
  receptive_field_size = 1
  if tensor.dim() > 2:
   receptive_field_size = tensor[0][0].numel()
  fan_in = num_input_fmaps * receptive_field_size
  fan_out = num_output_fmaps * receptive_field_size

 return fan_in, fan_out

xavier分布

xavier分布解析：https://prateekvjoshi.com/2016/03/29/understanding-xavier-initialization-in-deep-neural-networks/

假设使用的是sigmoid函数。当权重值(值指的是绝对值)过小，输入值每经过网络层，方差都会减少，每一层的加权和很小，在sigmoid函数0附件的区域相当于线性函数，失去了DNN的非线性性。

当权重的值过大，输入值经过每一层后方差会迅速上升，每层的输出值将会很大，此时每层的梯度将会趋近于0.

xavier初始化可以使得输入值x x x<math><semantics><mrow><mi>x</mi></mrow><annotation encoding="application/x-tex">x</annotation></semantics></math>x方差经过网络层后的输出值y y y<math><semantics><mrow><mi>y</mi></mrow><annotation encoding="application/x-tex">y</annotation></semantics></math>y方差不变。

（1）xavier的均匀分布

torch.nn.init.xavier_uniform_(tensor, gain=1)

也称为Glorot initialization。

>>> w = torch.empty(3, 5)
>>> nn.init.xavier_uniform_(w, gain=nn.init.calculate_gain('relu'))

(2) xavier正态分布

torch.nn.init.xavier_normal_(tensor, gain=1)

也称为Glorot initialization。

kaiming分布

Xavier在tanh中表现的很好，但在Relu激活函数中表现的很差，所何凯明提出了针对于relu的初始化方法。pytorch默认使用kaiming正态分布初始化卷积层参数。

(1) kaiming均匀分布

torch.nn.init.kaiming_uniform_
 (tensor, a=0, mode='fan_in', nonlinearity='leaky_relu')

也被称为 He initialization。

a – the negative slope of the rectifier used after this layer (0 for ReLU by default).激活函数的负斜率，

mode – either ‘fan_in' (default) or ‘fan_out'. Choosing fan_in preserves the magnitude of the variance of the weights in the forward pass. Choosing fan_out preserves the magnitudes in the backwards

pass.默认为fan_in模式，fan_in可以保持前向传播的权重方差的数量级，fan_out可以保持反向传播的权重方差的数量级。

>>> w = torch.empty(3, 5)
>>> nn.init.kaiming_uniform_(w, mode='fan_in', nonlinearity='relu')

(2) kaiming正态分布

torch.nn.init.kaiming_normal_
 (tensor, a=0, mode='fan_in', nonlinearity='leaky_relu')

也被称为 He initialization。

 >>> w = torch.empty(3, 5)
>>> nn.init.kaiming_normal_(w, mode='fan_out', nonlinearity='relu')

以上这篇对Pytorch神经网络初始化kaiming分布详解就是小编分享给大家的全部内容了，希望能给大家一个参考，也希望大家多多支持小牛知识库。