Python 实现3种回归模型（Linear Regression，Lasso，Ridge）的示例

公共的抽象基类

import numpy as np
from abc import ABCMeta, abstractmethod


class LinearModel(metaclass=ABCMeta):
 """
 Abstract base class of Linear Model.
 """

 def __init__(self):
  # Before fit or predict, please transform samples' mean to 0, var to 1.
  self.scaler = StandardScaler()

 @abstractmethod
 def fit(self, X, y):
  """fit func"""

 def predict(self, X):
  # before predict, you must run fit func.
  if not hasattr(self, 'coef_'):
   raise Exception('Please run `fit` before predict')

  X = self.scaler.transform(X)
  X = np.c_[np.ones(X.shape[0]), X]

  # `x @ y` == `np.dot(x, y)`
  return X @ self.coef_

Linear Regression

class LinearRegression(LinearModel):
 """
 Linear Regression.
 """

 def __init__(self):
  super().__init__()

 def fit(self, X, y):
  """
  :param X_: shape = (n_samples + 1, n_features)
  :param y: shape = (n_samples])
  :return: self
  """
  self.scaler.fit(X)
  X = self.scaler.transform(X)
  X = np.c_[np.ones(X.shape[0]), X]
  self.coef_ = np.linalg.inv(X.T @ X) @ X.T @ y
  return self

Lasso

class Lasso(LinearModel):
 """
 Lasso Regression, training by Coordinate Descent.
 cost = ||X @ coef_||^2 + alpha * ||coef_||_1
 """
 def __init__(self, alpha=1.0, n_iter=1000, e=0.1):
  self.alpha = alpha
  self.n_iter = n_iter
  self.e = e
  super().__init__()

 def fit(self, X, y):
  self.scaler.fit(X)
  X = self.scaler.transform(X)
  X = np.c_[np.ones(X.shape[0]), X]
  self.coef_ = np.zeros(X.shape[1])
  for _ in range(self.n_iter):
   z = np.sum(X * X, axis=0)
   tmp = np.zeros(X.shape[1])
   for k in range(X.shape[1]):
    wk = self.coef_[k]
    self.coef_[k] = 0
    p_k = X[:, k] @ (y - X @ self.coef_)
    if p_k < -self.alpha / 2:
     w_k = (p_k + self.alpha / 2) / z[k]
    elif p_k > self.alpha / 2:
     w_k = (p_k - self.alpha / 2) / z[k]
    else:
     w_k = 0
    tmp[k] = w_k
    self.coef_[k] = wk
   if np.linalg.norm(self.coef_ - tmp) < self.e:
    break
   self.coef_ = tmp
  return self

Ridge

class Ridge(LinearModel):
 """
 Ridge Regression.
 """

 def __init__(self, alpha=1.0):
  self.alpha = alpha
  super().__init__()

 def fit(self, X, y):
  """
  :param X_: shape = (n_samples + 1, n_features)
  :param y: shape = (n_samples])
  :return: self
  """
  self.scaler.fit(X)
  X = self.scaler.transform(X)
  X = np.c_[np.ones(X.shape[0]), X]
  self.coef_ = np.linalg.inv(
   X.T @ X + self.alpha * np.eye(X.shape[1])) @ X.T @ y
  return self

测试代码

import matplotlib.pyplot as plt
import numpy as np

def gen_reg_data():
 X = np.arange(0, 45, 0.1)
 X = X + np.random.random(size=X.shape[0]) * 20
 y = 2 * X + np.random.random(size=X.shape[0]) * 20 + 10
 return X, y

def test_linear_regression():
 clf = LinearRegression()
 X, y = gen_reg_data()
 clf.fit(X, y)
 plt.plot(X, y, '.')
 X_axis = np.arange(-5, 75, 0.1)
 plt.plot(X_axis, clf.predict(X_axis))
 plt.title("Linear Regression")
 plt.show()

def test_lasso():
 clf = Lasso()
 X, y = gen_reg_data()
 clf.fit(X, y)
 plt.plot(X, y, '.')
 X_axis = np.arange(-5, 75, 0.1)
 plt.plot(X_axis, clf.predict(X_axis))
 plt.title("Lasso")
 plt.show()

def test_ridge():
 clf = Ridge()
 X, y = gen_reg_data()
 clf.fit(X, y)
 plt.plot(X, y, '.')
 X_axis = np.arange(-5, 75, 0.1)
 plt.plot(X_axis, clf.predict(X_axis))
 plt.title("Ridge")
 plt.show()

测试效果

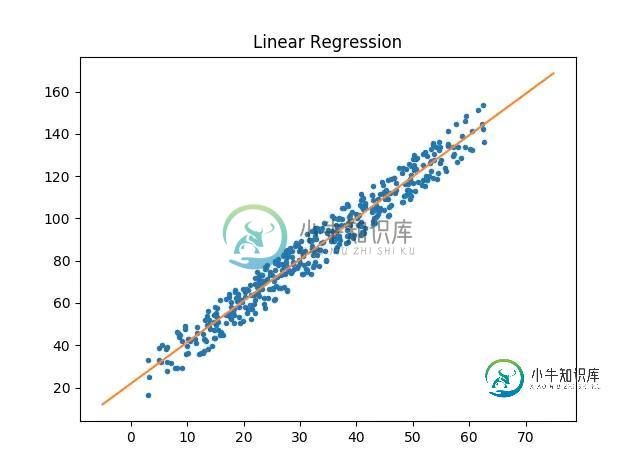
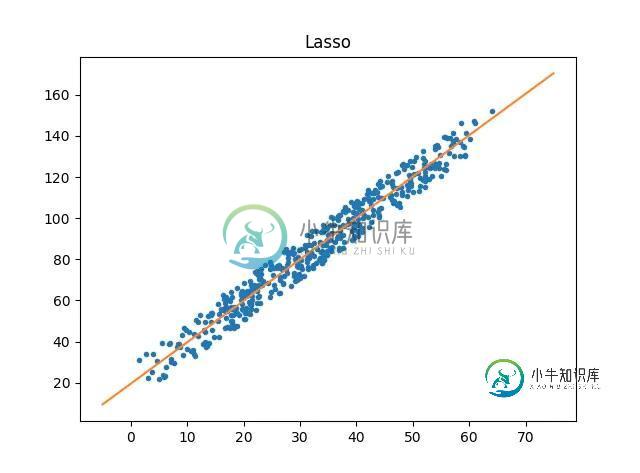
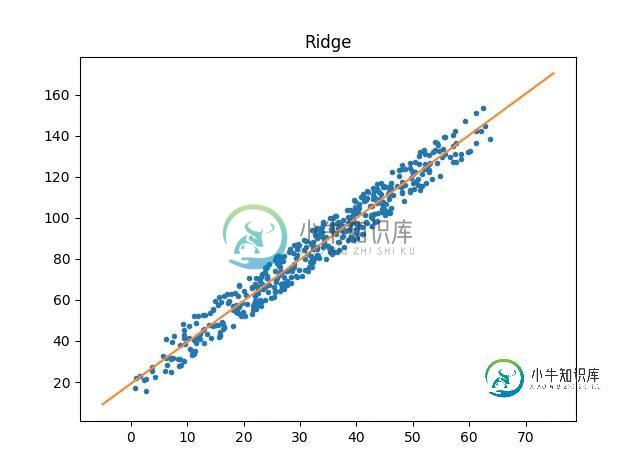
更多机器学习代码，请访问 https://github.com/WiseDoge/plume

以上就是Python 实现 3 种回归模型（Linear Regression，Lasso，Ridge）的示例的详细内容，更多关于Python 实现 回归模型的资料请关注小牛知识库其它相关文章！