python实现全排列代码(回溯、深度优先搜索)

从n个不同元素中任取m（m≤n）个元素，按照一定的顺序排列起来，叫做从n个不同元素中取出m个元素的一个排列。当m=n时所有的排列情况叫全排列。

公式：全排列数f(n)=n!(定义0!=1)

1 递归实现全排列（回溯思想）

1.1 思想

举个例子，比如你要对a,b,c三个字符进行全排列，那么它的全排列有abc,acb,bac,bca,cba,cab这六种可能就是当指针指向第一个元素a时，它可以是其本身a(即和自己进行交换)，还可以和b，c进行交换，故有3种可能，当第一个元素a确定以后，指针移向第二位置，第二个位置可以和其本身b及其后的元素c进行交换，又可以形成两种排列，当指针指向第三个元素c的时候，这个时候其后没有元素了，此时，则确定了一组排列，输出。但是每次输出后要把数组恢复为原来的样子。

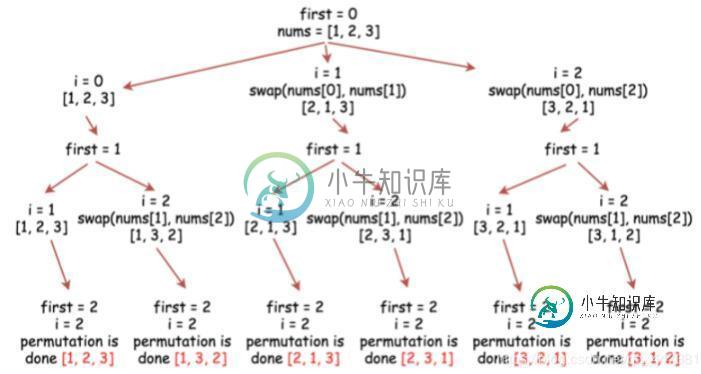
1.2 python实现

def permutations(arr, position, end):
  if position == end:
    print(arr)
  else:
    for index in range(position, end):
      arr[index], arr[position] = arr[position], arr[index]
      permutations(arr, position + 1, end)
      arr[index], arr[position] = arr[position], arr[index] # 还原到交换前的状态，为了进行下一次交换
 
 
arr = [1, 2, 3, 4]
permutations(arr, 0, len(arr))

2 深度优先搜索（DFS）实现全排列

2.1 思想

定义全排列问题：输入一个长度为n的列表arr，输出arr的全排列。

（1）首先可以确定的是，每一种全排列的结果中包含的列表长度均是n。想象面前有n个空盒子，现在要把这n个数放到这些空盒子里去，每个盒子只能放一个数。那么第一个盒子中可以放的选择是n种，可以使用一个循环来逐个尝试。

for index in range(0, len(arr)):
temp[position] = arr[index]

（2）第一个盒子放完后，就该往第二个盒子里放了。假设第一个盒子里放的是arr的第一个数，那么第二个盒子就只能放第2~n个数了（不能重复）。为此引入visit列表用来标记arr中哪些数字被使用过了。初始化：

visit = [True, True, True, True]

这样，当第一个位置已经使用过时，就在visit里做标记：visit = [False, True, True, True]

因此放第一个盒子的代码可以改写如下：

  for index in range(0, len(arr)):
    if visit[index] == True:
      temp[position] = arr[index]
      visit[index] = False

（3）当第k个盒子处理完毕后，处理下一个盒子直接调用dfs(k+1)即可，也就是递归调用。解决了当下该如何做，下一步也就知道怎么做了。

（4）递归调用的一定要注意的问题是递归调用的出口，否则循环调用下去程序会崩溃无法运行。在这个问题中什么时候结束递归调用呢？答案是当这n个盒子都放满了，即处理到第n+1个盒子时结束调用，同时输出此时的排列结果。

2.2 python实现

visit = [True, True, True, True]
temp = ["" for x in range(0, 4)]
 
 
def dfs(position):
  # 递归出口
  if position == len(arr):
    print(temp)
    return
  # 递归主体
  for index in range(0, len(arr)):
    if visit[index] == True:
      temp[position] = arr[index]
      visit[index] = False # 试探 
      dfs(position + 1)
      visit[index] = True # 回溯。非常重要
 
 
arr = [1, 2, 3, 4]
dfs(0)

注释了“非常重要”的语句是不能省略的，省略后仅出现[1, 2, 3, 4]一条结果。dfs(k+1)前后的两条语句分别称之为试探和回溯。

3 combination和permutations函数的区别

permutations方法重在排列：

import itertools
n=3
a=[str(i) for i in range(n)]
s=""
s=s.join(a)
for i in itertools.permutations(s,n):
  print (''.join(i))
 
# 结果  
012
021
102
120
201
210

combinations方法重在组合：

import itertools
n=3
a=[str(i) for i in range(n)]
s=""
s=s.join(a)
for i in itertools.combinations(s,n):
  print (''.join(i))
 
# 结果  
012

以上这篇python实现全排列代码(回溯、深度优先搜索)就是小编分享给大家的全部内容了，希望能给大家一个参考，也希望大家多多支持小牛知识库。