python可视化实现KNN算法

简介

这里通过python的绘图工具Matplotlib包可视化实现机器学习中的KNN算法。

需要提前安装python的Numpy和Matplotlib包。

KNN–最近邻分类算法，算法逻辑比较简单，思路如下：

1.设一待分类数据iData,先计算其到已标记数据集中每个数据的距离，例如欧拉距离sqrt((x1-x2)^2+(y1-y2)^2)；

2.然后根据离iData最近的k个数据的分类，出现次数最多的类别定为iData的分类。

KNN——最近邻算法python代码

代码实现：

import numpy as np
import matplotlib as mpl
import matplotlib.pyplot as plt

def KNNClassify(labelData,predData,k): #数据集包含分类属性
#labelData 是已经标记分类的数据集
#predData 未分类的待预测数据集
 labShape = labelData.shape
 for i in range(predData.shape[0]): #以predData的每行数据进行遍历
 iData = predData[i]
 iDset = np.tile(iData,(labShape[0],1)) #将iData重复，扩展成与labelData同形的矩阵
 #这里用欧拉距离sqrt((x1-x2)^2+(y1-y2)^2)
 diff = iDset[...,:-1] - labelData[...,:-1]
 diff = diff**2
 distance = np.sum(diff,axis=1)
 distance = distance ** 0.5 #开根号
 sortedIND = np.argsort(distance) #排序，以序号返回。
 classCount = { }
 for j in range(k): #计算距离最近的前k个标记数据的类别
 voteLabel = labelData[sortedIND[j],-1]
 classCount[voteLabel] = classCount.get(voteLabel,0)+1

 maxcls = max(classCount,key=classCount.get) #类别最多的，返回键名（类别名）
 predData[i][...,-1] = maxcls

 return predData

为了测试这个算法，需要现成的已分类数据集，由于手动输入很有限，数据量少，耗时。作为学习我们这里用代码模拟生成数据来进行测试。下面是生成已分类数据集的代码：

生成模拟数据的函数

import numpy as np
import matplotlib as mpl
import matplotlib.pyplot as plt

#模拟生成分类数据
#目标是产生二维坐标中的几堆数据集，每堆为一个类
#函数逻辑：
#将x轴分段，每个段设一个中心的，所有的中心点用cores存储。
#设置每个数据中心点core的类别，由中心点在一定范围内随机产生数据，并将这些数据设为和core一样的类别
#所以每类的数据会简单的被X轴的每段大致分开

def makeKNNData(colnum,clsnum,nums,cores = []):
#colnum单个数据拥有特征数量（包括数据的分类）；
# clsnum表示共有多少种分类；
# nums是一个元组，表示每个类别希望产生多少数据样本，如colnum为5，nums为[56, 69, 60, 92, 95]；
#cores非必要参数，手动给出只是用于测试，cores提供每类的中心点，以中心点为依据产生该类数据。

 dataSet = np.zeros((sum(nums),colnum)) #初始化数据集，用于存放随后生成的所有数据
 n=0 #记录生成数据的下标
 step = 20/clsnum #假定X坐标轴只显示0~20的范围，step为X轴分段后的段长
 for j in range(clsnum): #循环生成各个类数据
 try:
 core = cores[j] #如果cores没有给出则，则出错，跳至except执行
 except IndexError :
 core = np.random.rand(1,3) #中心点为array([[x1,x2,c]])，c用于表示类别，这里产生的是1*3的二维数组
 core[0][0] =j*step + core[0][0]*step #将x1限制在各段中
 core[0][1] *=15 #将x2即y轴限制在0~15范围内
 core[0][2] = j #设置类别
 cores.append(core)
 for i in range(nums[j]): #按nums中指定了每类数据的数量，用循环生成。
 point= core[0][:2] + np.random.rand(1,2)*step -step/2 #产生点point（x,y)，x以中心点在（core_x - step/2, core_x + step/2)范围随机波动，y同理。
 row = np.column_stack((point,core[0][2])) #加上类别成为一个数据
 dataSet[n] = row
 n +=1
 i +=1

 j +=1

 #print("print cores:",cores)
 return dataSet

有了数据集之后，我们可以用Matplotlib将数据可视化，以直观显示出来

数据可视化函数

import numpy as np
import matplotlib as mpl
import matplotlib.pyplot as plt

#绘图展示数据，每类数据点以不同的颜色显示
def showFigure(dataSet,clsnum):
 fig = plt.figure()
 ax = fig.add_subplot(1,1,1) #界面只需显示一个视图
 ax.set_title('KNN separable data set') #视图名称，这里简单统一定这个名称吧
 plt.xlabel('X') #坐标轴名称
 plt.ylabel('Y')

 colors = ['r','g','b','y','k'] #定义显示的颜色b为blue，k为black
 for i in range(clsnum):
 idx = np.where(dataSet[:,2] == i) #查询每类的索引号
 ax.scatter(dataSet[idx,0], dataSet[idx,1], marker='o', color=colors[i%5], label=1, s=10) #在视图中的显示方式

 plt.legend(loc = 'upper right') #图例显示位置
 plt.show()


#测试一下
#需要结合模拟生成数据的函数
classnum = 5
nums = np.random.randint(50,100,classnum) #示例 array([56, 69, 60, 92, 95])，每个数字在50~100范围内
dataSet = makeKNNData(3,classnum,nums)
showFigure(dataSet,classnum)

生成的模拟数据展示结果如下：

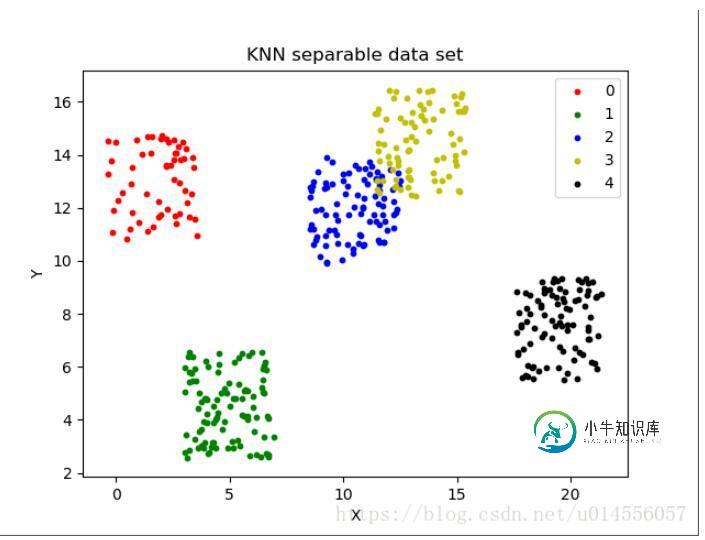
完整代码

import numpy as np
import matplotlib as mpl
import matplotlib.pyplot as plt

#模拟生成分类数据
#目标是产生二维坐标中的几堆数据集，每堆为一个类
#函数逻辑：
#将x轴分段，每个段设一个中心的，所有的中心点用cores存储。
#设置每个数据中心点core的类别，由中心点在一定范围内随机产生数据，并将这些数据设为和core一样的类别
#所以每类的数据会简单的被X轴的每段大致分开

def makeKNNData(colnum,clsnum,nums,cores = []):
#colnum单个数据拥有特征数量（包括数据的分类）；
# clsnum表示共有多少种分类；
# nums是一个元组，表示每个类别希望产生多少数据样本；
#cores非必要参数，手动给出只是用于测试，cores提供每类的中心点，以中心点为依据产生该类数据。

 dataSet = np.zeros((sum(nums),colnum)) #初始化数据集，用于存放随后生成的所有数据
 n=0 #记录生成数据的下标
 step = 20/clsnum #假定X坐标轴只显示0~20的范围，step为X轴分段后的段长
 for j in range(clsnum): #循环生成各个类数据
 try:
 core = cores[j] #如果cores没有给出则，则出错，跳至except执行
 except IndexError :
 core = np.random.rand(1,3) #中心点为array([[x1,x2,c]])，c用于表示类别，这里产生的是1*3的二维数组
 core[0][0] =j*step + core[0][0]*step #将x1限制在各段中
 core[0][1] *=15 #将x2即y轴限制在0~15范围内
 core[0][2] = j #设置类别
 cores.append(core)
 for i in range(nums[j]): #按nums中指定了每类数据的数量，用循环生成。
 point= core[0][:2] + np.random.rand(1,2)*step -step/2 #产生点point（x,y)，x以中心点在（core_x - step/2, core_x + step/2)范围随机波动，y同理。
 row = np.column_stack((point,core[0][2])) #加上类别成为一个数据
 dataSet[n] = row
 n +=1
 i +=1

 j +=1

 #print("print cores:",cores)
 return dataSet

#绘图展示数据，每类数据点以不同的颜色显示
def showFigure(dataSet,clsnum):
 fig = plt.figure()
 ax = fig.add_subplot(1,1,1) #界面只需显示一个视图
 ax.set_title('KNN separable data set') #视图名称，这里简单统一定这个名称吧
 plt.xlabel('X') #坐标轴名称
 plt.ylabel('Y')

 colors = ['r','g','b','y','k'] #定义显示的颜色b为blue，k为black
 for i in range(clsnum):
 idx = np.where(dataSet[:,2] == i) #查询每类的索引号
 ax.scatter(dataSet[idx,0], dataSet[idx,1], marker='o', color=colors[i%5], label=1, s=10) #在视图中的显示方式

 plt.legend(loc = 'upper right') #图例显示位置
 plt.show()


#分类算法：
#待分类数据iData,先计算其到已标记数据集中每个数据的距离
#然后根据离iData最近的k个数据的分类，出现次数最多的类别定为iData的分类。

def KNNClassify(labelData,predData,k): #数据集包含分类属性
#labelData 是已经标记分类的数据集
#predData 待预测数据集
 labShape = labelData.shape
 for i in range(predData.shape[0]): #以predData的每行数据进行遍历
 iData = predData[i]
 iDset = np.tile(iData,(labShape[0],1)) #将iData重复，扩展成与labelData同形的矩阵
 #这里用欧拉距离sqrt((x1-x2)^2+(y1-y2)^2)
 diff = iDset[...,:-1] - labelData[...,:-1]
 diff = diff**2
 distance = np.sum(diff,axis=1)
 distance = distance ** 0.5 #开根号
 sortedIND = np.argsort(distance) #排序，以序号返回。
 classCount = { }
 for j in range(k): #计算距离最近的前k个标记数据的类别
 voteLabel = labelData[sortedIND[j],-1]
 classCount[voteLabel] = classCount.get(voteLabel,0)+1

 maxcls = max(classCount,key=classCount.get) #类别最多的，返回键名（类别名）
 predData[i][...,-1] = maxcls

 return predData

#测试
labNums = np.random.randint(50,200,classnum)
predNums = np.random.randint(10,80,classnum)
#cores = [np.array([[ 0.08321641, 12.22596938, 0. ]]), np.array([[9.99891798, 4.24009775, 1. ]]), np.array([[14.98097374, 9.80120399, 2. ]])]

labelData = makeKNNData(3,classnum,labNums)
showFigure(labelData,classnum)
predData = makeKNNData(3,classnum,predNums) #这里为了方便，不在写产生待分类数据的代码，只需用之前的函数并忽略其类别就好。
predData[...,-1]=0
showFigure(predData,classnum)

k = 10
KNNData = KNNClassify(labelData,predData,k)
showFigure(KNNData,classnum)

运行程序，结果如下：

1.labelData的数据（已知分类的数据） 

2.predData的数据（未标记的数据） 

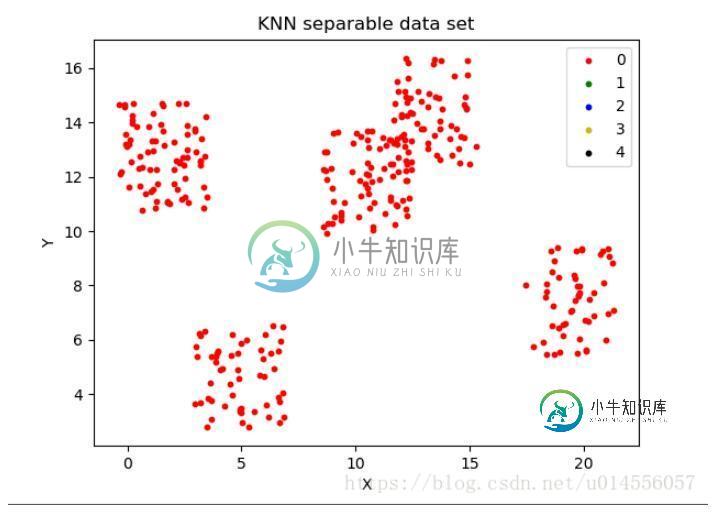
3KNNData的数据（用KNN算法进行分类后的数据）

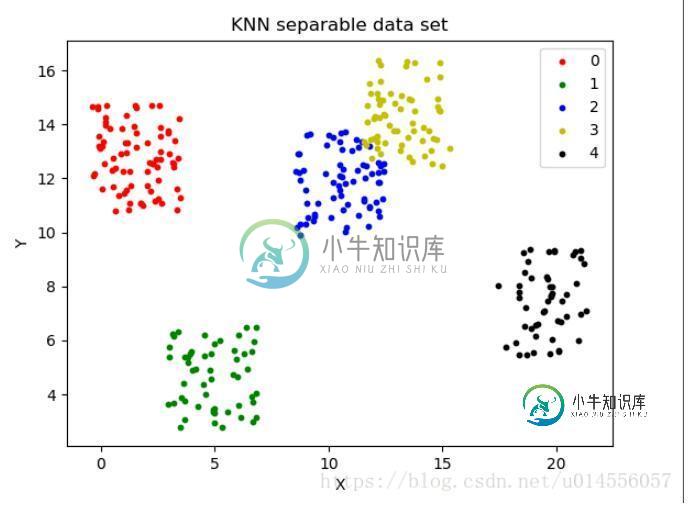
以上就是本文的全部内容，希望对大家的学习有所帮助，也希望大家多多支持小牛知识库。