Python实现的数据结构与算法之快速排序详解

本文实例讲述了Python实现的数据结构与算法之快速排序。分享给大家供大家参考。具体html" target="_blank">分析如下：

一、概述

快速排序（quick sort）是一种分治排序算法。该算法首先 选取 一个划分元素（partition element，有时又称为pivot）；接着重排列表将其 划分 为三个部分：left（小于划分元素pivot的部分）、划分元素pivot、right（大于划分元素pivot的部分），此时，划分元素pivot已经在列表的最终位置上；然后分别对left和right两个部分进行 递归排序。

其中，划分元素的 选取 直接影响到快速排序算法的效率，通常选择列表的第一个元素或者中间元素或者最后一个元素作为划分元素，当然也有更复杂的选择方式；划分 过程根据划分元素重排列表，是快速排序算法的关键所在，该过程的原理示意图如下：

<-- 选取划分元素 -->

<-- 划分过程 -->

<-- 划分结果 -->

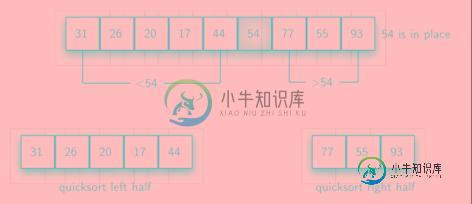
快速排序算法的优点是：原位排序（只使用很小的辅助栈），平均情况下的时间复杂度为 O(n log n)。快速排序算法的缺点是：它是不稳定的排序算法，最坏情况下的时间复杂度为 O(n2)。

二、Python实现

1、标准实现

#!/usr/bin/env python
# -*- coding: utf-8 -*-
def stdQuicksort(L):
  qsort(L, 0, len(L) - 1)
def qsort(L, first, last):
  if first < last:
    split = partition(L, first, last)
    qsort(L, first, split - 1)
    qsort(L, split + 1, last)
def partition(L, first, last):
  # 选取列表中的第一个元素作为划分元素
  pivot = L[first]
  leftmark = first + 1
  rightmark = last
  while True:
    while L[leftmark] <= pivot: 
 # 如果列表中存在与划分元素pivot相等的元素，让它位于left部分
     # 以下检测用于划分元素pivot是列表中的最大元素时，
  #防止leftmark越界
      if leftmark == rightmark:
        break
      leftmark += 1
    while L[rightmark] > pivot:
      # 这里不需要检测，划分元素pivot是列表中的最小元素时，
      # rightmark会自动停在first处
      rightmark -= 1
    if leftmark < rightmark:
      # 此时，leftmark处的元素大于pivot，
   #而rightmark处的元素小于等于pivot，交换二者
      L[leftmark], L[rightmark] = L[rightmark], L[leftmark]
    else:
      break
  # 交换first处的划分元素与rightmark处的元素
  L[first], L[rightmark] = L[rightmark], L[first]
  # 返回划分元素pivot的最终位置
  return rightmark

2、Pythonic实现

#!/usr/bin/env python
# -*- coding: utf-8 -*-
def pycQuicksort(L):
  if len(L) <= 1: return L
  return pycQuicksort([x for x in L if x < L[0]]) + \
      [x for x in L if x == L[0]] + \
      pycQuicksort([x for x in L if x > L[0]])

对比 标准实现 可以看出，Pythonic实现 更简洁、更直观、更酷。但需要指出的是，Pythonic实现 使用了Python中的 列表解析 （List Comprehension，也叫列表展开、列表推导），每一次 递归排序 都会产生新的列表，因此失去了快速排序算法本来的 原位排序 的优点。

三、算法测试

#!/usr/bin/env python
# -*- coding: utf-8 -*-
if __name__ == '__main__':
  L = [54, 26, 93, 17, 77, 31, 44, 55, 20]
  M = L[:]
  print('before stdQuicksort: ' + str(L))
  stdQuicksort(L)
  print('after stdQuicksort: ' + str(L))
  print('before pycQuicksort: ' + str(M))
  print('after pycQuicksort: ' + str(pycQuicksort(M)))

运行结果：

$ python testquicksort.py
before stdQuicksort: [54, 26, 93, 17, 77, 31, 44, 55, 20]
after stdQuicksort: [17, 20, 26, 31, 44, 54, 55, 77, 93]
before pycQuicksort: [54, 26, 93, 17, 77, 31, 44, 55, 20]
after pycQuicksort: [17, 20, 26, 31, 44, 54, 55, 77, 93]

希望本文所述对大家的Python程序设计有所帮助。