《无人车规划算法实习》专题
-
算法 - 目录
算法分析 排序 并查集 栈和队列 符号表 其它 参考资料 Sedgewick, Robert, and Kevin Wayne. Algorithms. Addison-Wesley Professional, 2011.
-
算法 - 排序
待排序的元素需要实现 Java 的 Comparable 接口,该接口有 compareTo() 方法,可以用它来判断两个元素的大小关系。 使用辅助函数 less() 和 swap() 来进行比较和交换的操作,使得代码的可读性和可移植性更好。 排序算法的成本模型是比较和交换的次数。 // java public abstract class Sort<t extends="" comparable
-
算法 - 其它
有三个柱子,分别为 from、buffer、to。需要将 from 上的圆盘全部移动到 to 上,并且要保证小圆盘始终在大圆盘上。 这是一个经典的递归问题,分为三步求解: ① 将 n-1 个圆盘从 from -> buffer ② 将 1 个圆盘从 from -> to ③ 将 n-1 个圆盘从 buffer -> to 如果只有一个圆盘,那么只需要进行一次移动操作。 从上面的讨论可以知道,an
-
Python Dijkstra算法
问题内容: 我正在尝试编写Dijkstra的算法,但是我在努力如何在代码中“说”某些事情而苦苦挣扎。为了可视化,这是我要使用数组表示的列: 因此,将有几个数组,如下面的代码所示: 粗体部分是我要坚持的地方-我正在尝试实现算法的这一部分: 3.对于当前节点,请考虑其所有未访问的邻居并计算其暂定距离。 例如,如果当前节点(A)的距离为6,并且将其与另一个节点(B)相连的边为2,则通过A到B的距离将为6
-
Jarvis March算法
本文向大家介绍Jarvis March算法,包括了Jarvis March算法的使用技巧和注意事项,需要的朋友参考一下 Jarvis March算法用于从一组给定的数据点中检测凸包的角点。 从数据集的最左端开始,我们通过逆时针旋转将这些点保留在凸包中。从当前点开始,我们可以通过从当前点检查这些点的方向来选择下一个点。当角度最大时,将选择该点。完成所有点后,当下一个点是起点时,停止算法。 输入输出
-
贪婪算法
本文向大家介绍贪婪算法相关面试题,主要包含被问及贪婪算法时的应答技巧和注意事项,需要的朋友参考一下 参考回答: 贪婪算法(贪心算法)是指在对问题进行求解时,在每一步选择中都采取最好或者最优(即最有利)的选择,从而希望能够导致结果是最好或者最优的算法。贪婪算法所得到的结果往往不是最优的结果(有时候会是最优解),但是都是相对近似(接近)最优解的结果。贪婪算法并没有固定的算法解决框架,算法的关键是贪婪策
-
排序算法
我想通过删除已经排序的项目来提高我的算法的效率,但是我不知道如何才能有效地做到这一点。我找到的唯一方法是重写整个列表。
-
组合算法
字段1,为true 字段2,真 字段3,false 字段4,false 字段5,false 结果是: {Field1,Field2,Field3,Field4,Field5} {Field1,Field2,,Field4,Field5} {Field1,Field2,,,Field5} {Field1,Field2,,,} {Field1,Field2,Field3,,Field5} {Field
-
变更算法
一个典型的变革问题,但有点扭曲。给定一个大的金额和面额,我需要想出总数的方式,其中金额可以使用RECURSION。函数的签名如下 总数 面额-可用面额。
-
杂耍算法
方法(一种杂耍算法)将数组划分为不同的集合,其中集合数等于n和d的GCD,并在集合内移动元素。如果GCD与上述示例数组(n=7,d=2)一样为1,则元素将仅在一个集合内移动,我们只需从temp=arr[0]开始,并将arr[I d]一直移动到arr[I],最后将temp存储在正确的位置。 以下是n=12和d=3的示例。GCD为3,且 设arr[]为{1,2,3,4,5,6,7,8,9,10,11,
-
Dijkstra SDSP算法
我试图使用邻接列表和PQ作为最小堆来实现单目标最短路径的Dijkstra算法。输出必须显示所有顶点到目标顶点的路径,如果路径存在,如果是,它的总和(最短),如果否,否路径。链接到整个代码 输入格式: 第一行是顶点数,n 第二行开始:(从1到n的顶点) 第一列是顶点 之后,多对, 根据GDB,它显示了在提取最小函数时发现的分段故障。 客户. c 从文本中提取输入。txt文件并创建一个有向图 服务器.
-
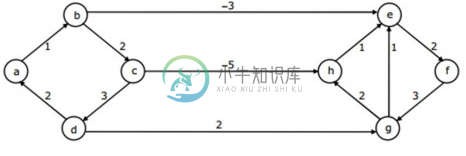 Dijkstra算法=SSSP
Dijkstra算法=SSSP据我所知,dijkstra无法处理负边权重。为此,我们必须使用贝尔曼福特。 Bellman fords在负边权重和负循环下运行良好,这是无法从源位置访问到的,否则,它将返回消息“负循环存在”。 但是,上面显示的图表与dijkstra运行良好,即使存在负边权重。那么,如何知道何时使用具有负边权重的dijkstra?? 我们想的是,dijkstra可以或不能使用负权重边。如果存在负循环,那么它将不起作
-
找峰算法
给定一个数组[a,b,c,d,e,f,G],其中a-g是数,b是峰当且仅当a<=b且b>=c。 他给出了一个递归的方法: 他说算法是T(n)=T(n/2)+o(1)=o(lgn) 在他的pdf中,他还给出了一个完整的例子: 他的定义是否意味着我们只需要找到一个峰? 我相信这个问题可以看作是在Riverst算法入门书中寻找最大和最小元素。
-
分治算法
几周前我有一个工作面试,我被要求设计一个分而治之的算法。我无法解决这个问题,但他们只是打电话给我进行第二次面试!问题是: 我们给出了两个n元素数组A[0..n-1]和B[0..n-1](它们不一定是排序的),以及一个整数值作为输入。给出了一个O(nlogn)分治算法,该算法确定是否存在不同的值i,j(即i!=j),使得A[i]+B[j]=value。如果i,j存在,算法应返回True,否则返回Fa
-
 算法面经
算法面经个人简介:双广州某985(2015-2022)、计算机硕士(保研)、CV方向、论文在投、YY算法岗3个月实习、国家级竞赛一二等奖(Robot CV相关)、研究生实验室个人项目、硕本GPA分别为3.61和3.37 秋招经历: ① 美团:到店平台技术部>ML/DM>二面后泡很久然后挂 ② 快手:机器学习算法岗>三面后泡很久然后挂 ③ 字节:抖音推荐算法岗>二面后挂(面试官迟到45min左右, 只面了1
