《贝壳找房》专题

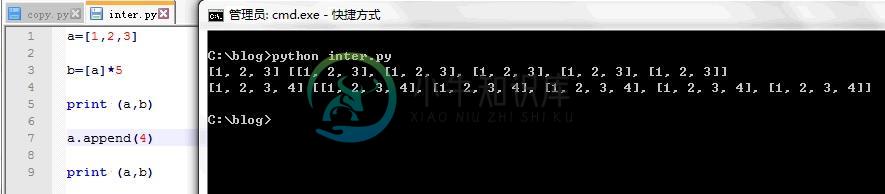
本文向大家介绍浅谈Python浅拷贝、深拷贝及引用机制，包括了浅谈Python浅拷贝、深拷贝及引用机制的使用技巧和注意事项，需要的朋友参考一下 这礼拜碰到一些问题，然后意识到基础知识一段时间没巩固的话，还是有遗忘的部分，还是需要温习，这里做份笔记，记录一下 前续 先简单描述下碰到的题目，要求是写出2个print的结果 可以看到，a指向了一个列表list对象，在Python中，这样的赋值语句，其实内

问题内容： 设置如下： 我有一个客户端的站点设置。客户： 访问该网站 输入我们的记录的基本信息 通过“立即购买”按钮进入贝宝 通过贝宝付款 返回网站 我想知道的是如何获得所有交易的清单？我拥有PayPal登录名以及API用户名，密码和签名，但是对于我来说，我一生中都找不到一个可以在互联网上找到单个位置的示例，该示例说明了如何通过PHP或PHP从PayPal中提取交易列表。 jQuery / Jav

本文向大家介绍angularJS深拷贝详解，包括了angularJS深拷贝详解的使用技巧和注意事项，需要的朋友参考一下 在了解angular深拷贝之前，首先看下边的代码。 很显然，输出的a的值是1，b的值是2。接下来再看一段代码。 很显然，输出a的值是[1,2,3,4,5]，b的值是[1,2,3,4,5]。再来看下一段代码。 很显然，输出的a和b的值都是{name:"lisi",age:30}。这

我正在工作的一个项目，需要贝宝的ACH支持。你能告诉我如何使用贝宝进行交易吗？ 我指的是以下链接：http://www.codeproject.com/articles/152280/online-credit-card-transaction-in-asp-net-using-pa 它正在使用PayFlow SDK，并做信用卡转账。我也能为阿奇做同样的事。但更大的问题是代码没有使用任何贝宝秘密/

我不小心从~/.kube/config中删除了配置文件。每个 kubectl 命令都由于缺少配置而失败。 示例: 与服务器localhost:8080的连接被拒绝-是否指定了正确的主机或端口？ 我已经使用以下方式安装了k3s： 和kubectl使用： 有人知道如何解决这个问题吗？

主要内容：索贝尔变体使用索贝尔(sobel)操作，可以在水平和垂直方向上检测图像的边缘。可以使用方法在图像上应用操作。以下是这种方法的语法 - 该方法接受以下参数 - src - 表示源(输入)图像的类的对象。 dst - 表示目标(输出)图像的类的对象。 ddepth - 表示图像深度的整数变量()。 dx - 表示导数的整数变量(或)。 dy - 表示导数的整数变量(或)。 示例 以下程序演示如何在给定图像上执行

引用和copy(),deepcopy()的区别 import copy a = [1, 2, 3, 4, ['a', 'b']] #原始对象 b = a #赋值，传对象的引用 c = copy.copy(a) #对象拷贝，浅拷贝 d = copy.deepcopy(a) #对象拷贝，深拷贝 a.append(5) #修改对象a a[4].append('c') #修改对象a中的['

问题内容： 所以我试图让Paypal按钮显示在我的应用程序上，但无法正常工作。我基于这个jsfiddle。 https://jsfiddle.net/rbacekkb/ 我试图放入我的应用程序，但该按钮没有显示在我想要的页面上。我不知道我做错了什么。 试图使其显示在当前页面上以进行测试。 index.html 问题答案： 似乎直到今天还没有人开发一个react的paypal按钮（对于react-n

当使用NodeJS SDK与PayPal的V2订单API集成时，什么时候是完成订单的正确时间（例如，向客户运送产品）。

我创建贝宝Restapi以下步骤1.创建登录ID由developer.paypal.com2.点击我的应用程序3.点击按钮"创建应用程序"创建测试应用程序4.通过单击testapp，我得到了两个api凭据（i）测试凭据（ii）实时凭据（通过单击显示） 我的代码中存在上述api（客户端ID和密码）的问题，代码给出的错误号为401或某个时间为400 我已检查“帐户资格” PayPal付款和登录与Pay

基础示例 <vuep template="#example"></vuep> <script v-pre type="text/x-template" id="example"> <template> <div class="amap-page-container"> <el-amap vid="amapDemo" :zoom="zoom" :center="center" c

贝叶斯决策论是概率框架下实施决策的基本方法。它假设决策问题可以用概率的形式来描述，并且假设所有有关的概率结构均已知。 贝叶斯决策论 假设$$\lambda_{ij}$$为真实标记为$$c_j$$的样本误分类为$$c_i$$所产生的损失，可以定义将样本x分类$$c_i$$的条件风险（即期望损失）为 $$R(ci|x) = \sum{j=1}^{N} \lambda_{ij}P(c_j|x)$$ 为最

创建一个对象的浅拷贝。 使用 Object.assign() 和一个空对象({})来创建原始对象的浅拷贝。 const shallowClone = obj => Object.assign({}, obj); const a = { x: true, y: 1 }; const b = shallowClone(a); // a !== b

校验者: @Kyrie 翻译者: @TWITCH 朴素贝叶斯方法是基于贝叶斯定理的一组有监督学习算法，即“简单”地假设每对特征之间相互独立。 给定一个类别 和一个从 到 的相关的特征向量， 贝叶斯定理阐述了以下关系: ![P(y \mid x_1, \dots, x_n) = \frac{P(y) P(x_1, \dots x_n \mid y)}

1、个人信息再确认，哪个学校毕业的，考研还是保研，以后打算读博还是工作etc 2、介绍你的研究方向 3、介绍下你的研究内容，另外发了论文没 4、常用的数据预处理方法有哪些 5、l1正则和l2正则哪个收敛更快？为什么 6、l1正则和l2正则哪个抑制过拟合效果更好？为什么 7、用过哪些网络 8、transformer了解吗？ 9、l1、l2在深层还是浅层抑制过拟合的效果好？ 10、dropout用过吗