使用迭代深化实现极小极大搜索

Question

我在做什么：我正在用C编写一个象棋引擎。我最近更新了我的引擎的minimax搜索算法，该算法使用alpha-beta修剪来利用迭代深化，以便在时间限制下运行。这是它的外观：

//I return a string, int pair. The string represents the best move found, while the int represents the engine evaluation for the node after said move is made

static std::pair<string, int> iterativeDeepeningSearch(Board initialPosition, int maxDepth, milliseconds maxSearchTime)
    {
        std::pair<string, int> bestMove;
        milliseconds startTime = duration_cast<milliseconds>(
            system_clock::now().time_since_epoch());

        for (int currentDepth = 1; currentDepth <= maxDepth; currentDepth++)
        {

            milliseconds currentTime = duration_cast<milliseconds>(
                system_clock::now().time_since_epoch());
            if (currentTime > startTime + maxSearchTime)
            {
                return bestMove;
            }
            std::pair<string, int> bestMoveFoundFromMinimax = minimax(initialPosition, currentDepth, INT_MIN, INT_MAX, "", "", startTime + maxSearchTime);
            if (bestMoveFoundFromMinimax.first != "") {
                bestMove = bestMoveFoundFromMinimax;
            }
        }
        return bestMove;
    }

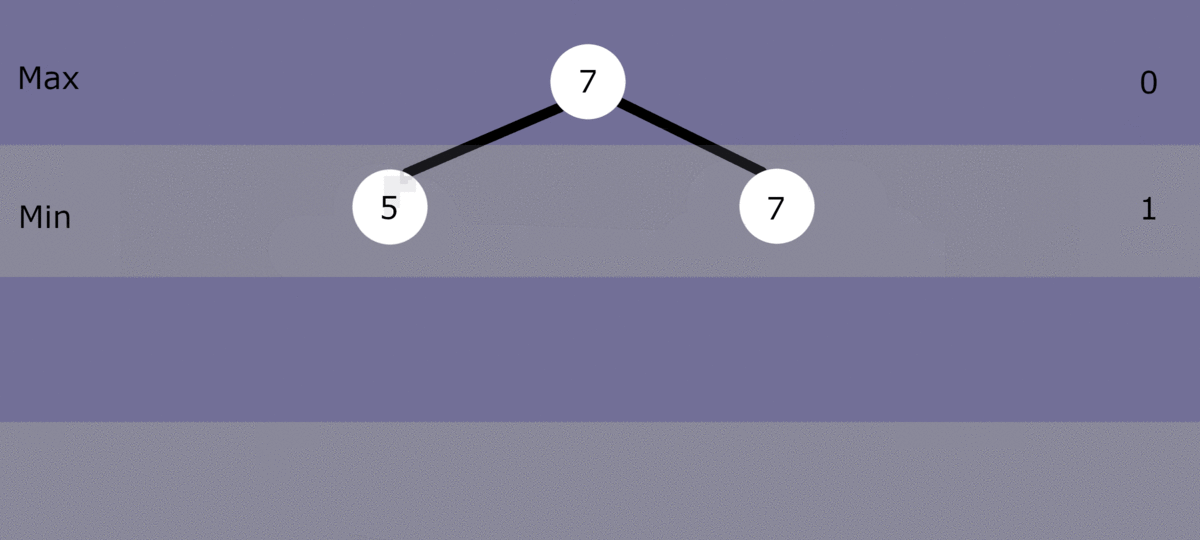
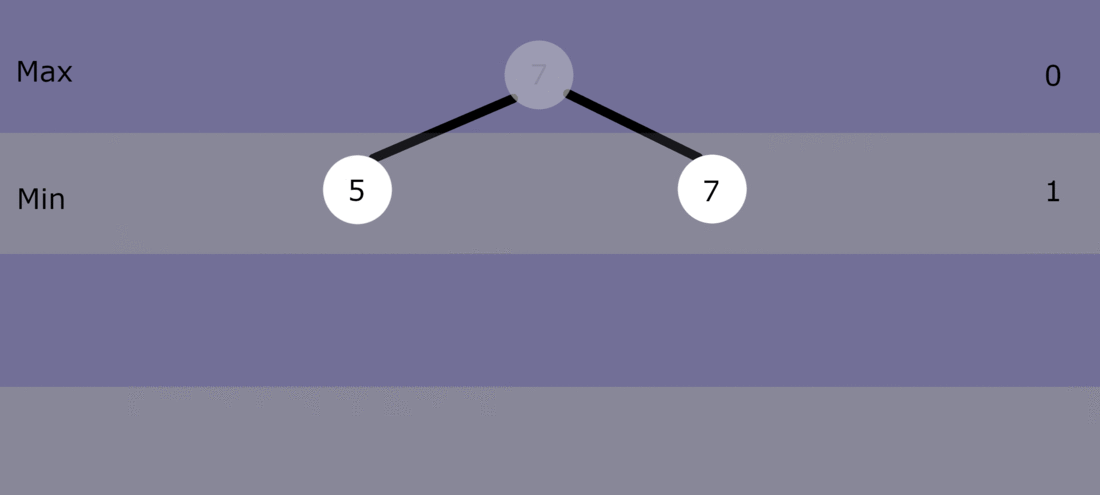
我的问题：这个实现的问题是，当搜索任何大于1的深度时，它将在搜索所需深度之前搜索所有之前的深度。也就是说，此迭代深化搜索首先搜索深度为1的所有移动。然后，它将再次搜索深度1，然后再搜索深度2，而不是在下一次搜索时选择深度2。然后，它将在搜索深度3之前搜索深度1和2。等等

我的问题是：这就是迭代深化的工作方式吗？每次增加深度时，我们也会搜索所有父节点？我设想，每次我们增加深度时，它只会在新深度搜索所有同级节点。如果这实际上是迭代深化的工作方式，那么如何只搜索新的深度而不搜索所有父节点呢？

作为参考，下面是我的（草率的）利用alpha-beta修剪的minimax函数：

static std::pair<string, int> minimax(Board node, int depth, int alpha, int beta, string move, string firstMove, milliseconds breakOffTime)
{
    if (breakOffTime != std::chrono::milliseconds(0))
    {
        milliseconds currentTime = duration_cast<milliseconds>(
            system_clock::now().time_since_epoch());
        if (currentTime > breakOffTime)
        {
            return std::make_pair("", 0);
        }
    }

    Moves &moves = Moves::getInstance();
    if (moves.isCheckmate(node))
    {
        if (node.getWhiteToMove())
        {
            return std::make_pair(firstMove, INT_MIN);
        }
        else
        {
            return std::make_pair(firstMove, INT_MAX);
        }
    }
    if (depth == 0)
    {
        return std::make_pair(firstMove, Rating::getCentipawnValue(node));
    }
    if (node.getWhiteToMove())
    {
        string bestMove = firstMove;
        int bestValue = INT_MIN;
        string pseudoLegalMoves = moves.pseudoLegalMovesW(node);
        if (pseudoLegalMoves.length() == 0)
        {
            return std::make_pair(firstMove, 0);
        }
        for (int i = 0; i < pseudoLegalMoves.length(); i += 4)
        {
            string individualMoveString;
            individualMoveString += pseudoLegalMoves[i];
            individualMoveString += pseudoLegalMoves[i + 1];
            individualMoveString += pseudoLegalMoves[i + 2];
            individualMoveString += pseudoLegalMoves[i + 3];
            Board tNode = moves.makeMoveAll(node, individualMoveString);
            if ((moves.unsafeForWhite(tNode) & tNode.getWK()) == 0)
            {
                std::pair<string, int> ab;
                if (firstMove == "")
                {
                    ab = minimax(tNode, depth - 1, alpha, beta, individualMoveString, individualMoveString, breakOffTime);
                }
                else
                {
                    ab = minimax(tNode, depth - 1, alpha, beta, individualMoveString, firstMove, breakOffTime);
                }
                int val = ab.second;
                string move = ab.first;
                if (val > bestValue || (val == bestValue && bestMove == ""))
                {
                    bestValue = val;
                    bestMove = move;
                }
                alpha = max(alpha, bestValue);
                if (alpha >= beta)
                {
                    break;
                }
            }
        }
        return std::make_pair(bestMove, bestValue);
    }
    else
    {
        string bestMove = firstMove;
        int bestValue = INT_MAX;
        string pseudoLegalMoves = moves.pseudoLegalMovesB(node);
        if (pseudoLegalMoves.length() == 0)
        {
            return std::make_pair(firstMove, 0);
        }
        for (int i = 0; i < pseudoLegalMoves.length(); i += 4)
        {
            string individualMoveString;
            individualMoveString += pseudoLegalMoves[i];
            individualMoveString += pseudoLegalMoves[i + 1];
            individualMoveString += pseudoLegalMoves[i + 2];
            individualMoveString += pseudoLegalMoves[i + 3];
            Board tNode = moves.makeMoveAll(node, individualMoveString);
            if ((moves.unsafeForBlack(tNode) & tNode.getBK()) == 0)
            {
                std::pair<string, int> ab;
                if (firstMove == "")
                {
                    ab = minimax(tNode, depth - 1, alpha, beta, individualMoveString, individualMoveString, breakOffTime);
                }
                else
                {
                    ab = minimax(tNode, depth - 1, alpha, beta, individualMoveString, firstMove, breakOffTime);
                }
                int val = ab.second;
                string move = ab.first;
                if (val < bestValue || (val == bestValue && bestMove == ""))
                {
                    bestValue = ab.second;
                    bestMove = ab.first;
                }
                beta = min(beta, bestValue);
                if (alpha >= beta)
                {
                    break;
                }
            }
        }
        return std::make_pair(bestMove, bestValue);
    }
}

此外，如果有人有兴趣检查它，这是我的完整项目：https://github.com/ChopinDavid/Maestro-cpp

我不是C开发人员，所以这可能很糟糕。

Answer 1

这就是迭代深化的工作方式吗？每次增加深度时，我们也会搜索所有父节点？

是的-但是由于您在进行迭代深化时保存了之前搜索中的最佳移动，并且会在向下的过程中首先尝试这些移动，因此您通常会在每个级别的第一个移动中找到最佳移动，因此修剪将非常有效。

如何只搜索新的深度而不是搜索所有的父节点？

如果这是您想要的，您可以放弃迭代深化，只需按您想要的深度进行一次搜索，但这可能是一个错误。在使用该解决方案之前，先计算有无迭代深化的评估板的数量。