未优化路线的最小成本流
我正在尝试使用MinCostFlow或工具解决一个工程问题。有一个带有管道和多个供应阀的机械分配系统。这些阀门需要连接到用户。起初,我试图用匈牙利算法来解决这个问题,但后来我意识到,这并不考虑通过路径的流。
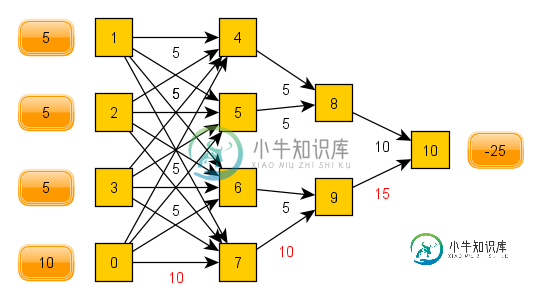
节点0-4是消费者,节点4-7是供应阀,节点8和9是管道。我在每个消费者身上放了一个“供应”,以显示它期望的流量。我在最后放了一个水槽,以将供应从系统中取出。并非所有消费者都有相同的需求。我们可以看到节点0需要10,我专门设计了一条路径(用红色突出显示),允许它将其带到那里。我暂时将所有价格设置为0。
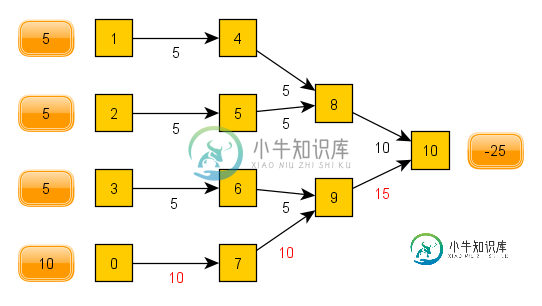
然而,它实际上是这样解决的:
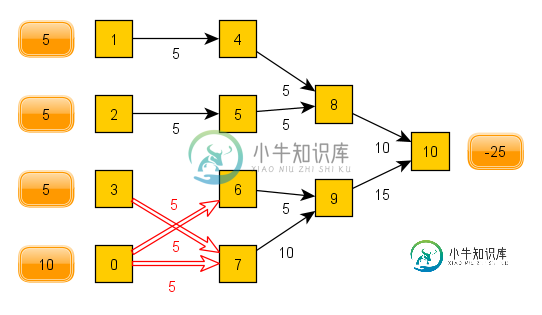
出于某种原因,它决定将节点0拆分为两个节点(6和7),然后让较大的节点7从3和0接收5。从系统的角度来看,这并不理想,我不明白为什么它会以这种方式解决它。在匈牙利算法中,它不允许工人接受多个工作。在该算法中,节点4-7是工作者,节点0-3是作业。
我可以通过将弧的成本从节点1-3增加到节点7来获得所需的结果,但我不想操纵成本字段来获得所需的结果。这似乎需要很多额外的工作来帮助优化工具选择正确的路径。
我如何使用或工具来实现这一点?
共有1个答案
为了简单起见,只要您希望解算器选择路径,它就会变成NP完全。最小成本流是多项式,根据定义,它将跨弧分割流,而不选择其中一个。
您想要的是整数线性问题。您可以使用CP-SAT求解器或使用CBC的线性求解器包装器或CP-SAT作为后端来解决它。
-
通过系统内置规则,将匹配规则的闲置浪费或安全性较低的资源扫描出来并按照建议进行处理,从而达到节约成本、提高资源安全性的目的。 建议列表 建议列表显示所有匹配优化建议规则的资源列表,用户可根据建议对资源进行处理。 忽略列表 忽略列表显示不需要处理的资源或一类规则建议。 规则配置 规则配置即针对不同资源的使用情况设置对应的规则,当资源匹配规则代表资源需要按照费用优化进行优化。
-
这是最小成本路径动态规划问题的一个变体,让我难倒了。 我得到了一个成本矩阵MXN。成本矩阵有随机放置的正缓冲区和负成本。我从[1,1]开始,必须到[m,n]。我从一个初始缓冲区x开始。在我的遍历过程中,我的缓冲区x永远不应该<=0。如果它变成<=0,那么即使结束状态是一个正缓冲区,也是一个无效的路径(把它想象成一个玩家从一些初始健康开始,负成本扣除健康,而正缓冲区增加健康)。什么是最小的初始缓冲区
-
我遇到了这个问题: 你必须乘坐一辆汽车穿过城市的
-
我有一个最小成本流网络,其中一些弧有固定费用,也就是说,如果弧有非零流量,那么成本是c\u k,与流量无关。0的流产生0的成本。这些圆弧没有容量限制。 我知道如何将其建模为一个混合整数程序(MIP):添加一个0/1变量,成本为c\k。将arc上的容量设置为M*y\U k,其中M大于所有电源的总和。因此,当且仅当弧有流时,才会产生固定成本。 是否可以使用最小成本流公式来解决此问题,该公式比一般MIP
-
1 原理 给定n个带权的观察样本$(w_i,a_i,b_i)$: $w_i$表示第i个观察样本的权重; $a_i$表示第i个观察样本的特征向量; $b_i$表示第i个观察样本的标签。 每个观察样本的特征数是m。我们使用下面的带权最小二乘公式作为目标函数: minimize{x}\frac{1}{2} \sum{i=1}^n \frac{wi(a_i^T x -b_i)^2}{\sum{k=
-
给了我一个问题,上面写着: 给定一个具有整数权值(正负两种)的连通有向图,发展一种求两顶点之间最短路径的算法。 我想我可以使用最小生成树算法,比如Kruskal的算法,然后用Dijkstra的算法来证明,因为在MST中,每个顶点只有一条内边,Dijkstra的算法即使在负权值下也能工作。 这听起来像是共食吗? 附注。我很难证明MST包含有向图的每个顶点的最短路径。

