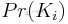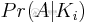阵列保持不变的概率是多少？

Question

这个问题在微软的采访中被问到过。非常好奇为什么这些人会问这么奇怪的概率问题？

给定一个兰特（N），一个随机生成器，它生成从0到N-1的随机数。

int A[N]; // An array of size N
for(i = 0; i < N; i++)
{
    int m = rand(N);
    int n = rand(N);
    swap(A[m],A[n]);
}

编辑：请注意，种子不是固定的。

数组A保持不变的概率是多少？
假设数组包含唯一元素。

Answer 1

下面是C代码，用于计算rand可以生成的2N个索引元组的值的数量，并计算概率。从N=0开始，它显示1、1、8、135、4480、189125和12450816的计数，概率为1、1、。5.185185, .0683594, .0193664，以及。计数没有出现在整数序列百科全书中，所以要么我的程序有错误，要么这是一个非常模糊的问题。如果是这样的话，这个问题不是求职者想要解决的，而是要暴露他们的一些思维过程，以及他们如何应对挫折。我认为这不是一个好的面试问题。

#include <inttypes.h>
#include <math.h>
#include <stdint.h>
#include <stdio.h>
#include <stdlib.h>


#define swap(a, b)  do { int t = (a); (a) = (b); (b) = t; } while (0)


static uint64_t count(int n)
{
    // Initialize count of how many times the original order is the result.
    uint64_t c = 0;

    // Allocate space for selectors and initialize them to zero.
    int *r = calloc(2*n, sizeof *r);

    // Allocate space for array to be swapped.
    int *A = malloc(n * sizeof *A);

    if (!A || !r)
    {
        fprintf(stderr, "Out of memory.\n");
        exit(EXIT_FAILURE);
    }

    // Iterate through all values of selectors.
    while (1)
    {
        // Initialize A to show original order.
        for (int i = 0; i < n; ++i)
            A[i] = i;

        // Test current selector values by executing the swap sequence.
        for (int i = 0; i < 2*n; i += 2)
        {
            int m = r[i+0];
            int n = r[i+1];
            swap(A[m], A[n]);
        }

        // If array is in original order, increment counter.
        ++c;    // Assume all elements are in place.
        for (int i = 0; i < n; ++i)
            if (A[i] != i)
            {
                // If any element is out of place, cancel assumption and exit.
                --c;
                break;
            }

        // Increment the selectors, odometer style.
        int i;
        for (i = 0; i < 2*n; ++i)
            // Stop when a selector increases without wrapping.
            if (++r[i] < n)
                break;
            else
                // Wrap this selector to zero and continue.
                r[i] = 0;

        // Exit the routine when the last selector wraps.
        if (2*n <= i)
        {
            free(A);
            free(r);
            return c;
        }
    }
}


int main(void)
{
    for (int n = 0; n < 7; ++n)
    {
        uint64_t c = count(n);
        printf("N = %d:  %" PRId64 " times, %g probabilty.\n",
            n, c, c/pow(n, 2*n));
    }

    return 0;
}

Answer 2

很好奇为什么这些人会问这么奇怪的概率问题？

问这样的问题是因为它们能让面试官深入了解被面试者的想法

• 能够阅读代码（非常简单的代码，但至少是一些东西）
• 能够分析算法以识别执行路径
• 运用逻辑寻找可能结果和边缘案例的技能
• 推理和解决问题的能力
• 沟通和工作技能-他们会问问题，还是根据手头的信息孤立工作

... 等等要想提出一个能够揭示受访者这些属性的问题，关键是要有一段看似简单的代码。这就把冒名顶替者甩掉了，而非编码者被卡住了；傲慢的人会跳到错误的结论；懒散或差强人意的计算机科学家找到了一个简单的解决方案并停止寻找。通常，正如他们所说，不是你是否得到了正确的答案，而是你的思维过程是否给人留下深刻印象。

我也会尝试回答这个问题。在面试中，我会解释自己，而不是提供一行字的书面答案——这是因为即使我的“答案”是错误的，我也能够展示逻辑思维。

A将保持不变，即元素处于相同位置

• 在每次迭代中，m==n（这样每个元素只与自身交换）；或

第一种情况是duedl0r给出的“简单”情况，即数组没有改变。这可能是答案，因为

数组A保持不变的概率是多少？

如果数组在i=1处更改，然后在i=2处恢复，则它处于原始状态，但并没有“保持不变”——它被更改，然后更改回来。这可能是一个聪明的技术问题。

然后考虑到元素被交换和交换回来的可能性，我认为在一次采访中，这种计算超出了我的能力范围。显而易见的考虑因素是，这不需要进行“更改-更改回交换”，也可以很容易地在三个元素之间进行交换，交换1和2，然后是2和3，1和3，最后是2和3。接下来，可能会有4个、5个或更多像这样的“循环”项目之间的互换。

事实上，与其考虑数组不变的情况，不如考虑它被改变的情况可能更简单。考虑这个问题是否可以映射到像帕斯卡三角形这样的已知结构上。

这是一个很难的问题。我同意在面试中解决这个问题太难了，但这并不意味着在面试中问这个问题太难了。可怜的候选人不会有答案，一般的候选人会猜测明显的答案，好的候选人会解释为什么这个问题太难回答。

我认为这是一个“开放式”问题，可以让面试官深入了解候选人。因此，尽管在面试中很难解决这个问题，但这是一个很好的面试问题。问问题不仅仅是检查答案是对还是错。

Answer 3

嗯，我玩得很开心。当我第一次读到这个问题时，我想到的第一件事是群论（尤其是对称群S_{n）。for循环通过在每次迭代中组合换位（即交换），简单地在Sn中构建置换σ。我的数学不是那么精彩，而且我有点生疏，所以如果我的记数法不正确的话，请原谅我}

设A为数组在置换后保持不变的事件。我们最终被要求找出事件发生的概率。

我的解决方案尝试遵循以下步骤：

1. 考虑所有可能的排列（即我们数组的重新排序）
2. 根据它们包含的所谓身份转置的数量将这些排列划分为不相交的集合。这有助于将问题减少到仅偶数排列。
3. 给定置换为偶数（并且具有特定长度），确定获得单位置换的概率。
4. 对这些概率求和，得到数组不变的总概率。

请注意，for循环的每次迭代都会创建一个交换（或换位），它会导致两件事中的一件（但决不能同时产生两件）：

1. 两个元素交换
2. 元素与自身交换。出于我们的意图和目的，数组是不变的

我们标记第二种情况。让我们定义一个身份换位如下：

当一个数字与其自身交换时，就会发生身份转换。也就是说，当上述for循环中的n==m时。

对于所列代码的任何给定运行，我们组成了N个换位。可以有<代码>0，1，2，在这个“链”中出现的身份转换的N。

例如，考虑N=3的情况：

Given our input [0, 1, 2].
Swap (0 1) and get [1, 0, 2].
Swap (1 1) and get [1, 0, 2]. ** Here is an identity **
Swap (2 2) and get [1, 0, 2]. ** And another **

请注意，存在奇数个非身份转置（1），数组已更改。

设K\u i为在给定置换中出现身份置换的事件。注：这构成了所有可能结果的详尽划分：

• 任何置换都不能同时具有两个不同数量的身份置换，并且
• 所有可能的置换必须具有介于0和N之间的身份置换

因此，我们可以应用总概率定律：

现在我们终于可以利用分区了。请注意，当非身份转置的数量为奇数时，数组不可能保持不变*。因此：

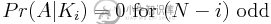
*从群论来看，排列是偶数还是奇数，但决不能两者兼而有之。因此，奇数置换不能是身份置换（因为身份置换是偶数）

因此，我们现在必须确定N-i的两个偶数概率：

1. 
2. 

• 结果与之前的结果无关，并且
• 创建身份换位的概率相同，即1/N。

因此，对于N个试验，获得身份转换的概率为：

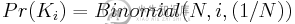
首先考虑置换（n，m）和等价置换（m，n）。然后，设M为可能的非身份置换数。我们将经常使用这个数量。

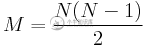
这里的目标是确定换位集合可以组合成身份置换的方式的数量。我将尝试构建一个N=4的一般解。

让我们考虑一下所有身份转换（即i=N=4）的情况。让X表示一个身份转换。对于每个X，都有N种可能性（它们是：N=m=0，1，2，…，N-1）。因此，存在实现身份置换的可能性。为了完整性，我们添加二项式系数C（N，i），以考虑身份转置的顺序（这里它正好等于1）。我试图通过上述元素的物理布局和以下可能性的数量来描述这一点：

I  =  _X_   _X_   _X_   _X_
       N  *  N  *  N  *  N  * C(4, 4) => N^N * C(N, N) possibilities

现在，不必显式地替换N=4和i=4，我们可以查看一般情况。将上述内容与之前发现的分母相结合，我们发现：

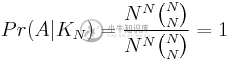
这是直观的。事实上，除了1之外的任何其他值都可能会引起您的警觉。想想看：我们被赋予了所有N转置都被称为标识的情况。在这种情况下数组不变的可能性是多少？显然，1。

现在，对于N=4，我们再来考虑2个身份转换（即i=N-2=2）。按照惯例，我们将把这两个标识放在末尾（并说明以后的排序）。我们现在知道，我们需要选择两个换位，当它们组合起来时，将成为身份置换。让我们将任何元素放置在第一个位置，称之为t1。如上所述，如果t1不是一个身份（不能是我们已经放置的两个身份），那么就有M的可能性。

I  =  _t1_   ___   _X_   _X_
       M   *  ?  *  N  *  N

第二个点中可能剩下的唯一元素是t1的倒数，实际上是t1的倒数（这是唯一的倒数）。我们再次加入二项式系数：在这种情况下，我们有4个开放位置，我们希望放置2个身份置换。我们有多少方法可以做到这一点？4选择2。

I  =  _t1_   _t1_   _X_   _X_ 
       M   *  1   *  N  *  N  * C(4, 2) => C(N, N-2) * M * N^(N-2) possibilities

再看看一般情况，这一切都对应于：

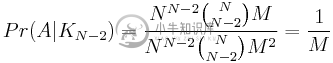
最后，我们做了没有身份换位的N=4案例（即i=N-4=0）。由于有很多可能性，它开始变得棘手，我们必须小心不要重复计数。我们以类似的方式开始，将单个元素放在第一个位置并计算出可能的组合。首先采取最简单的方法：相同的换位4次。

I  =  _t1_   _t1_   _t1_   _t1_ 
       M   *  1   *  1   *  1   => M possibilities

现在让我们考虑两个唯一的元素t1和t2。t1有M可能性，t2只有M-1可能性（因为t2不能等于t1）。如果我们穷尽所有安排，我们将剩下以下模式：

I  =  _t1_   _t1_   _t2_   _t2_ 
       M   *  1   *  M-1 *  1   => M * (M - 1) possibilities   (1)st

   =  _t1_   _t2_   _t1_   _t2_
       M   *  M-1 *  1   *  1   => M * (M - 1) possibilities   (2)nd

   =  _t1_   _t2_   _t2_   _t1_
       M   *  M-1 *  1   *  1   => M * (M - 1) possibilities   (3)rd

现在让我们考虑三个独特的元素，t1，t2，t3。让我们先放置t1，然后放置t2。与往常一样，我们有：

I  =  _t1_   _t2_   ___   ___ 
       M   *  ?   *  ?  *  ?  

我们还不能说还可能有多少个t2，我们将在一分钟内看到原因。

我们现在将t1排在第三位。请注意，t1必须到达那里，因为如果要进入最后一个位置，我们只需重新创建上面的第三条安排。重复计算很糟糕！这会将第三个唯一元素t3保留到最终位置。

I  =  _t1_   _t2_   _t1_   _t3_ 
       M   *  ?   *  1  *   ?  

那么，我们为什么要花一分钟来更仔细地考虑t2s的数量呢？换位t1和t2不能是不相交的排列（即，它们必须共享一个（并且只有一个，因为它们也不能相等）n或m）。这是因为如果它们不相交，我们可以交换排列顺序。这意味着我们将重复计算st安排。

说t1=（n，m）<对于某些x和y，代码t2的形式必须为（n，x）或（y，m）才能不相交。请注意，x可能不是n或m，y可能不是n或m。因此，t2可能是的可能置换的数量实际上是2*（N-2）。

那么，回到我们的布局：

I  =  _t1_    _t2_    _t1_   _t3_ 
       M   * 2(N-2) *  1   *  ?  

现在，t3必须与t1 t2 t1的组成相反。让我们手动完成：

(n, m)(n, x)(n, m) = (m, x) 

因此，t3必须是（m，x）。注意，这与t1不相交，也不等于t1或t2，因此这种情况下不存在重复计算。

I  =  _t1_    _t2_    _t1_   _t3_ 
       M   * 2(N-2) *  1  *   1    => M * 2(N - 2) possibilities   

最后，把所有这些放在一起：

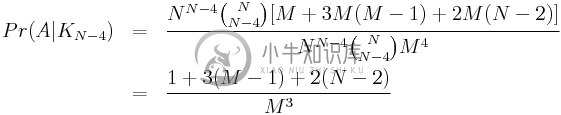
就是这样。倒向工作，将我们发现的内容替换为步骤2中给出的原始总和。我计算了下面N=4的情况的答案。它与另一个答案中的经验数字非常接近！

         N  =  4
         M  =  6   _________ _____________ _________
                  | Pr(K_i) | Pr(A | K_i) | Product | 
         _________|_________|_____________|_________|
        |         |         |             |         |
        |  i = 0  |  0.316  |  120 / 1296 |  0.029  |
        |_________|_________|_____________|_________|
        |         |         |             |         |
        |  i = 2  |  0.211  |    6 / 36   |  0.035  |
        |_________|_________|_____________|_________|
        |         |         |             |         |
        |  i = 4  |  0.004  |    1 / 1    |  0.004  |
        |_________|_________|_____________|_________|
                            |             |         |
                            |     Sum:    |  0.068  |
                            |_____________|_________|

如果群论能在这里得到应用，那就太酷了——也许真的有！这当然有助于彻底消除所有这些繁琐的计数（并将问题缩短到更加优雅的程度）。我在N=4时停止工作。对于<代码>N

无论如何，我绝对不能在面试的范围内做这样的事情。如果我幸运的话，我会走到分母的那一步。除此之外，这似乎很讨厌。