一种将图划分为完全子图的算法

Question

我需要一个算法来将无向图的顶点划分为一个或多个子图，这样每个子图都是一个完整的图（每个顶点与每个其他顶点相邻）。每个顶点都需要恰好位于其中一个子图中。

这里有一个例子：

input = [
    (A, B),
    (B, C),
    (A, C),
    (B, D),
    (D, E),
]
output = myalgo(input)  # [(A, B, C), (D, E)]

下面的图片更好地描述了这个问题：

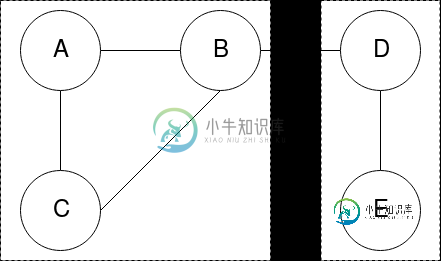
Kosaraju算法：它只适用于有向图。

Answer 1

这里有一个类，它实现了对完整子图的分段。它绝不是最优化的，可能会得到显著的改进，但这是一个起点

class SCCManager:
    def __init__(self, edges):
        self.clusters = []
        self.edges = edges

    def clusters_in(self, conn):
        first, second = conn
        f_clust = None
        s_clust = None
        for i, clust in enumerate(self.clusters):
            if first in clust:
                f_clust = i
            if second in clust:
                s_clust = i
            # break early if both already found
            if f_clust and s_clust:
                break
        return (f_clust, s_clust)

    def all_connected(self, cluster, vertex):
        for v in cluster:
            connected = (v, vertex) in self.edges or (vertex, v) in self.edges
            # break early if any element is not connected to the candidate
            if not connected:
                return False
        return True

    def get_scc(self):
        for edge in self.edges:
            c_first, c_second = self.clusters_in(edge)

            # case 1: none of the vertices are in an existing cluster
            # -> create new cluster containing the vertices
            if c_first == c_second == None:
                self.clusters.append([edge[0], edge[1]])
                continue

            # case 2: first is in a cluster, second isn't
            # -> add to cluster if eligible
            if c_first != None and c_second == None:
                # check if the second is connected to all cluster components
                okay = self.all_connected(self.clusters[c_first], edge[1])
                # add to cluster if eligible
                if okay:
                    self.clusters[c_first].append(edge[1])
                continue

            # case 3: other way round
            if c_first == None and c_second != None:
                okay = self.all_connected(self.clusters[c_second], edge[0])
                if okay:
                    self.clusters[c_second].append(edge[0])
                continue

            # case 4: both are in different clusters
            # -> merge clusters if allowed
            if c_first != c_second:
                # check if clusters can be merged
                for v in self.clusters[c_first]:
                    merge = self.all_connected(self.clusters[c_second], v)
                    # break if any elements are not connected
                    if not merge:
                        break
                # merge if allowed
                if merge:
                    self.clusters[c_first].extend(self.clusters[c_second])
                    self.clusters.remove(self.clusters[c_second])

            # case 5: both are in the same cluster
            # won't happen if input is sane, but doesn't require an action either way


        return self.clusters

...这里有一个工作示例：

inp = [
    ('A', 'B'),
    ('B', 'C'),
    ('A', 'C'),
    ('B', 'D'),
    ('D', 'E'),
    ('C', 'E')
]

test = SCCManager(inp)
print(test.get_scc())

[['A', 'B', 'C'], ['D', 'E']]