计算心率从ECG流-java/Nymi乐队

Question

我试图使用Nymi波段提供的ECG数据流来计算用户的心率。我目前的方法是通过Nymi Bands ECG流获取10秒的ECG数据样本，检查心跳并乘以6得到BPM。通过从当前值中减去之前的值并将其存储在一个列表中，我得到了一个相当精确的ECG流图。问题是，我很难准确地确定心跳实际发生的时间。

我的猜测是，我需要首先应用某种形式的过滤器，以确保“噪音”不会对读数产生负面影响。所以我的问题是：有没有更干净、更准确的方法来分析可能的心跳数据？或者我怎样才能正确地过滤数据以消除“噪音”？

编辑1（代码和样本数据）：

第一种方法：我使用Chauvenet标准的变体来尝试捕捉异常值，这将代表心跳。然而，标准偏差总是太高，平均值太低（几乎总是负值），无法准确检测出哪些值是异常值。使用示例数据（如下），结果是10秒内22拍：

private List<Integer> parseDataForHB(List<Integer> ecgValues)
{
    double mean = mean(ecgValues);
    double standardDeviation = standardDeviation(ecgValues);
    Iterator it = ecgValues.iterator();

    List<Integer> heartBeatValues = new ArrayList<>();

    NormalDistribution normalDistribution = new NormalDistribution(mean, standardDeviation);
    while(it.hasNext())
    {
        int ecgVal = (Integer) it.next();
        stringBuilder.append(", " + ecgVal);

        if((normalDistribution.cumulativeProbability((double)ecgVal) * ecgValues.size()) < 0.5)
        {
            heartBeatValues.add(ecgVal);
        }
    }
    return heartBeatValues;
}

-第二种方法：双重通过，找到平均心跳值。第一关；使用整个数据集的最大值作为“起始平均值”，然后查找至少为最大值1/2的所有值，该数据用于为第一遍检测到的所有节拍创建平均值。第二关；再次遍历所有值，查找至少为新平均值50%的任何值。这已被证明比第一种方法更准确，但仍然错误地检测/丢弃心跳。使用样本数据（如下），结果为10秒内7次：

private List<Integer> parseDataForHB(List<Integer> ecgValues, int averageHeartBeatValue)
{
    int previousVal = 0;
    List<Integer> heartBeatValues = new ArrayList<>();
    Iterator it = ecgValues.iterator();

    while(it.hasNext())
    {
        int ecgVal = (Integer)it.next();
        if(ecgVal >= (averageHeartBeatValue * .5))
        {
            if(((ecgVal > 0) && (previousVal < 0)) ||
                    ((ecgVal < 0) && (previousVal > 0)))
            {
                heartBeatValues.add(ecgVal);
                averageHeartBeatValue = (int) mean(heartBeatValues);
            }
        }
        previousVal = ecgVal;
    }
    return  heartBeatValues;
}

样本数据（绘制图表时，有10个可见的尖峰，代表心跳）：

-59752, -66222, -45702, -34272, -25891, -19203, -13547, -12212, -5916, -8793, -5083, -2075, 3231, 6295, 4898, 3029, 3427, 2161, 4274, -1209, 3428, -1793, 2560, 5195, 1092, 8088, 7539, 6673, 7338, 8527, 11586, 12264, 7979, 4316, 8383, 3198, 2555, 3574, 753, 2964, -3042, 901, -3218, -6178, -21116, 24346, -602, -1520, -3454, -1430, -7914, -1906, -6920, -8216, -8013, -6836, -7863, -1031, 3049, -271, -1010, 1562, -166, -1069, 1143, 3268, -1074, -258, -749, 433, -450, 2612, -2582, 1063, -2656, 3751, -1608, 637, -997, -7, 1155, -556, -1397, 2807, -967, 2946, 1198, -1133, -11066, 5439, 11159, -1066, 643, -34, 441, 1378, 1451, -1664, -2054, -2390, -1484, -1227, 5589, 5151, 4068, 3040, -2243, 1762, -2942, 51, 1793, 245, 171, 639, -375, 1296, -1327, 729, -624, -2642, 3964, -2641, 286, -2766, -393, -316, 2343, -3658, -552, 613, 2687, -1347, 539, -11251, 2873, 14529, -5234, -919, -2486, -3641, 4647, 0, -2149, -4063, -2619, -749, 18, 5274, 6670, 1413, 2697, 2673, 157, -180, 166, 2352, 454, 2013, -2867, 3788, -423, 1680, 1167, -1282, 1554, 768, 298, 205, -480, 2618, 531, -839, -1067, -1056, 1693, 3300, 52, -2087, 259, -5031, -4896, 15720, -3576, -3005, 849, -2643, 2204, -4461, -1953, -572, -3743, -3664, -2254, 3326, 7791, 2388, -1847, 2592, -1142, -1550, 1224, -1044, -1698, -481, 1469, -479, -125, -1853, 455, -38, 167, -55, -2126, -2291, 96, 1179, -2948, -1960, -876, 29, -2660, 1465, -1025, -2131, 2058, -3111, -19865, 20644, 1786, -2853, -2190, -2047, -1873, -643, -921, -3191, -3524, -5160, -3216, 2431, 7117, 1796, 2435, -516, 1557, -1248, -2745, -860, -618, -565, -93, 602, -3364, -1658, 1398, -126, -1715, -1685, 680, -1805, 232, -2093, -1703, -2844, -628, -2049, -1450, 1737, -1216, 2681, -2963, -4605, -11062, 15109, 133, -3804, -2971, -1867, -194, -1433, -4328, -2887, -4452, -3241, -1997, 1815, 6139, 1655, 1583, 520, -2574, -2458, 299, -2345, -475, 991, -2273, -1038, -154, 267, -1528, -1720, -440, -77, -1717, -28, -2684, -606, -1862, -560, -2120, -900, -4206, 2636, -8, -917, -1249, -3586, -13119, 8999, 6520, -2474, -3229, -1804, -1933, -1104, -3035, -1307, -3457, -4996, -2804, -2841, 3889, 6843, 1992, -671, 548, -1871, -2000, 1441, -1519, -2303, -1067, 1131, -1001, -1396, -289, -968, 1864, -3006, -1918, -72, -239, -589, -2233, -1982, 2608, -2765, -1461, -2215, -1916, 2924, -13, 342, -446, -3427, -19378, 20846, 2310, -6999, -1806, -728, -932, -2081, -2129, -2054, -4103, -2641, -4826, 1457, 3338, 6764, 2363, -1811, 453, -2577, -796, -237, -663, -1594, -170, -922, -149, -2258, -816, -1250, -1640, 2522, -4363, 668, -3494, -557, -21, -263, -4197, 694, -2921, -161, -3000, -852, 3120, 339, -1138, -2066, -4505, -13751, 17435, -446, -4212, -1339, -2239, -223, -1322, -3550, -3987, -2102, -3505, -3971, 3695, 3535, 3150, 2459, 1575, -3297, -383, -1470, 1556, -2191, -123, -1444, -1572, 1973, -3773, 1206, -860, -1384, -395, -818, -934, -940, -494, 795, -1416, -3613, -442, 622, -2798, 1296, -373, -400, -1270, 278, -5536, -14798, 20071, -2973, -3795, -754, -3358, -393, -2279, -1834, -1983, -5568, -4118, -2595, 1443, 6367, 3245, 1500, -1697, 1287

这个数据样本有更多的“噪音”，理想情况下我想过滤掉：

-35751, -32565, -28033, -23493, -18135, -10310, -8731, -4143, -5485, -2162, -955, -6393, -4211, -3047, -3097, -3232, -2975, -1571, -2105, -1440, -3880, -372, -227, -1266, -2269, -299, 2255, -2534, -3677, 675, 78, 415, -2274, -2256, 875, -13756, -5896, 15991, 585, -4356, 2706, -2028, 2127, -2249, -1282, -2555, -2865, -2570, -2666, 3745, 5965, 2728, -73, 611, 342, 1297, 214, -1153, 496, -283, -1868, 1791, -541, 2044, -414, 1595, 72, -2262, -363, 1855, -649, 909, -815, -363, 2791, 152, 1072, -2025, 1291, -12311, -6729, 22739, -4036, -784, 2598, -871, -2182, 1244, -2158, -2403, -1551, -3825, -4385, 4281, 5919, 6609, -2120, 480, 1070, -736, 525, -1520, -2225, 1795, 574, 781, -584, -1750, 175, 3339, -1175, 1186, -1319, 361, 885, -46, -1078, -2569, -720, 1533, 2465, 113, -1953, 2475, -5732, -22272, 24177, 235, 1385, -3850, 2291, -1417, -2452, -862, -3745, -932, -3586, -3987, -69, 5431, 3902, 2284, -619, 609, -1424, -1467, -1055, -1166, -1216, 1515, -1851,  -49, -4983, 1495, 3563, -873, -1933, -397, -933, 546, -1925, -753, -53, -2603, -591, 769, 3005, -2773, 2097, -5993, -21911, 23700, 3747, -4986, 595, -1815, -1589, -571, -2116, -1823, -6708, -1686, -1891, -991, 5178, 3719, 1188, -2394, 3992, -1555, -5306, 2830, 25, -2564, 2112, -1723, -3810, 4700, -2780, 520, -70, -2015, 1093, -2231, 2526,  -4651, -799, 764, -2429, 272, -564, 1119, -1089, 2371, -5627, -8118, 7574, 6499, -8635, 582, -2186, -1986, -477, -2178, -707, -6743, -3582,  -4409, 1806, 2718, 5820, -272, 1046, -580, -1552, -1184, -3206, -690, 1218, -871, -1919, -2552, 2127, -754, -1848, -3573, 3112, -1170, 468, -2593, -382, -3280, 3664, -5572, 1992, -30, -7230, 8670, -2504, -4969, -14813, 225, 14109, 8194, -9438, -4781, 3102, -8626, 6428, -5387, -5050, 548, -10060, 6965, -2155, 2195, 5498, 359, -4090, 5130, -4214, 1478, -364, -6444, 5889, -3363, -1621, -3570, 8390, -5828, -1472, 841, -8869, 11057, -6734, 173, 535, -638, -2628, -2751, 4754, 514, -2423, 1168, -3860, -23875, 18070, 7511, -3048, -1173, -6033, 5087, -5258, -3012, -831, -1180, -5298, -557, -2993, 6236, 1417, 2683, 361, 2293, -4117, 1122, -1922, -3730, 2705, -848, -3560, 2100, -319, -495, -347, -2329, 1341, -805, 1227, -2463, -440, -1440, 1206, -2361, -411, -1481, 3837, -3101, 1851, -5779, -22183, 22335, 3443, -3854, -2077, -2311, 1471, -817, 792, -7227, -2963, -4038, -92, -1234, 4692, 3973, 2122, 1333, -222, -2997, 1279, -3531, 1335, 140, -375, -2235, 2795, 598, -3233, -951, 1895, -288, -925, 1066, -3400, -1230, -2011, 2217, 1942, -1790, -1700, -1450, 756, -10710, -6744, 18590, -1435, -1739, -2097, -2638, -454, 67, -4556, -695, -5602, -2815, -2142, 764, 5958, 2175, 2055, -647, -466, -478, -1082, 527, -2214, 275, 274, -1687, -2358, 31, 1570, -1587, -871, -271, -2365, 1337, -831, -1095, -2056, -208, -1383, 2415, -1523, -1538, -719, -3842, -20933, 15223, 9978, -4030, -2521, 190, -4163, -2305, 1814, -2465, -4207, -3792, -2559, -2123, 2908, 5366, 2933, -1455, -57, 112, -2241, -1416, -2778, 2353, -1200, -2027, -962, 1117, -1530, 157, -2902, 3466, -5072, 555, 1425, -2791, -1369, 156, -6789, 1961, -1111, 3631, -2592, -1643, 2039, -2865

更新1-根据@stackoverflow user2010的建议，我尝试使用FFS将ECG数据转换成频谱，以计算实际频率的峰值。然而，当通过方法1（肖维内准则）或方法2（基于平均心跳值的计算）时，这里的结果并没有好多少。也许我遗漏了什么？以下是使用相同数据集的结果：

转换类型。前进：进近1=1，进近2=266

TransformType.逆：进场1=1，进场2=0

我认为部分问题是为了使用FFT，数据必须是2的幂。由于数据流的大小不同（记录10秒，更快的心跳将生成更大的数据集），如果数据集的大小不是2的幂，我必须填充数据集的末尾。

下面是FFT功能的新代码：

 private List<Integer> ffs(List<Integer> ecgValues)
{
    List<Integer> transoformedStream = new ArrayList<>();
    FastFourierTransformer ffs = new FastFourierTransformer(DftNormalization.STANDARD);
    double[] input = convertToDoubleArray(ecgValues);

    Complex[] complex = ffs.transform(input, TransformType.FORWARD);

    for(int i = 0; i < complex.length - 1; i++)
    {
        double real = (complex[i].getReal());
        double imaginary = (complex[i].getImaginary());

        transoformedStream.add((int)Math.sqrt((real * real) + (imaginary * imaginary)));
    }

    return transoformedStream;
}

private double[] convertToDoubleArray(List<Integer> ecgValues)
{
    double[] convertedList;

    if(isPowerOfTwo(ecgValues.size()))
    {
        convertedList = new double[ecgValues.size()];
    }
    else
    {
        convertedList = new double[nextPowerOfTwo(ecgValues.size())];
    }

    for(int i = 0; i < ecgValues.size(); i++)
    {
        convertedList[i] = (double)ecgValues.get(i);
    }
    return convertedList;
}

private boolean isPowerOfTwo(int size)
{
    boolean isPowerOfTwo = ((size & -size) == size);

    return isPowerOfTwo;
}

private int nextPowerOfTwo(int size)
{
    int res = 2;
    while (res <= size) {
        res  *= 2;
    }

    return res;
}

对方法2代码中的while循环稍作修改：

while(it.hasNext())
    {
        int ecgVal = (Integer)it.next();
        if(ecgVal >= (averageHeartBeatValue * .5))
        {
                heartBeatValues.add(ecgVal);
                averageHeartBeatValue = (int) mean(heartBeatValues);
        }
    }

更新2-继续处理FFT数据，但仍不确定我是否在正确的道路上。使用上面列出的用于FFT的相同方法（使用org.apache.commons.math3.transform.FastFourierTransex），我在FFT结果中搜索峰值。由于这个值太高，我遵循了我发现的另一种方法，在这里您将峰值乘以信号频率（在本例中为50），并除以样本大小。对于下面的示例，计算如下：

50hz*423079（峰值）/510（样本量）=41478.33

或者：

50hz*179（峰值指数）/510（样本量）=17.54

以下是ECG值：

-70756.0, -56465.0, -52389.0, -25199.0, -20352.0, -13660.0, -12615.0, -9202.0, -10225.0, -6168.0, -5338.0, 4409.0, -1204.0, 3009.0, 1821.0, -3127.0, 2076.0, 720.0, 675.0, -880.0, 622.0, 1851.0, -915.0, 1296.0, -3069.0, -10.0, 1114.0, 2335.0, -4363.0, 3386.0, -189.0, -2497.0, 6326.0, -4007.0, -2708.0, 1120.0, -2159.0, 2643.0, -1817.0, 749.0, 6096.0, -2927.0, -1514.0, -24006.0, 18897.0, 10851.0, -2934.0, -1487.0, -1660.0, 90.0, 1999.0, -4448.0, 2567.0, -1185.0, -2172.0, -4479.0, -253.0, 5173.0, 5956.0, 2814.0, 3279.0, 1617.0, 5174.0, -4152.0, 911.0, 2404.0, 1579.0, 792.0, 573.0, -28.0, 3251.0, 159.0, -2170.0, 727.0, 2652.0, -2676.0, 3039.0, -2938.0, 2539.0, 1586.0, -1447.0, 132.0, -60.0, 439.0, -87.0, -2239.0, 2074.0, 1268.0, -3559.0, 1266.0, -18937.0, -869.0, 25032.0, -6298.0, -1653.0, 590.0, -1737.0, -3840.0, -484.0, -3408.0, -2470.0, -3663.0, -1526.0, -158.0, -748.0, 5249.0, -44.0, 1903.0, -1900.0, 2513.0, -58.0, -2065.0, -450.0, -1131.0, -2262.0, 3663.0, -2968.0, 1262.0, -1687.0, -2745.0, -581.0, -11.0, -528.0, 349.0, -2231.0, -1198.0, -2039.0, 1362.0, -3671.0, 580.0, -794.0, -3924.0, -1711.0, 2093.0, -935.0, 2423.0, -1017.0, -5674.0, -26830.0, 27284.0, 4433.0, -4604.0, -2655.0, -4541.0, -2643.0, 2036.0, -3159.0, -3194.0, -2030.0, -2535.0, -5753.0, -31.0, 5056.0, 241.0, 4452.0, -1591.0, -1056.0, 573.0, -3637.0, -1224.0, -2728.0, 3535.0, -2645.0, -1281.0, -1359.0, -1918.0, 621.0, -2967.0, 2535.0, -3048.0, -2820.0, -2530.0, -1202.0, 315.0, -645.0, -3541.0, -3547.0, -2725.0, -4590.0, -124.0, 620.0, -1866.0, -4450.0, -17536.0, 4480.0, 16119.0, -7421.0, 2363.0, -8373.0, 3109.0, -896.0, -6533.0, -1502.0, -378.0, -3602.0, -5893.0, -2730.0, 2619.0, 3532.0, 675.0, -778.0, -590.0, 288.0, -3793.0, -3934.0, -830.0, 564.0, -1103.0, -5270.0, 121.0, 950.0, -2570.0, -502.0, -1556.0, -142.0, -1683.0, -2455.0, -3154.0, -2773.0, -2883.0, -1375.0, -2866.0, -5988.0, 1914.0, -2311.0, -1654.0, -2757.0, -4321.0, -29329.0, 26384.0, 2636.0, -5619.0, -3352.0, -5555.0, -72.0, -5429.0, -751.0, -2445.0, -8749.0, -4021.0, -912.0, -2294.0, 6468.0, 135.0, 1281.0, -2321.0, -320.0, -2578.0, -3737.0, -1470.0, -1841.0, -631.0, -1108.0, -2371.0, -2055.0, -3166.0, -1419.0, -677.0, -3666.0, -881.0, -20.0, -4403.0, 1366.0, -3804.0, 1064.0, -10377.0, 4307.0, -3898.0, -845.0, 3795.0, -7509.0, -21636.0, 12672.0, 9857.0, -2862.0, -4136.0, -1805.0, -5989.0, 410.0, 1048.0, -13174.0, -949.0, -3802.0, -4939.0, 1437.0, -506.0, 1305.0, 6104.0, -1481.0, -3925.0, 1949.0, -1001.0, -4920.0, -172.0, -1043.0, -1158.0, -2925.0, -994.0, -2615.0, 720.0, -8393.0, 3785.0, -3428.0, -7614.0, 5963.0, -1540.0, -4688.0, -722.0, 881.0, -4912.0, 2058.0, -493.0, -7200.0, 4413.0, -34168.0, 29170.0, 1335.0, -4874.0, -13611.0, 8360.0, -4880.0, 1229.0, -4077.0, -7090.0, 4488.0, -8641.0, -3558.0, -2288.0, 3415.0, -1972.0, 4252.0, -578.0, -2509.0, -1106.0, -297.0, -3186.0, 1630.0, -5392.0, 261.0, -446.0, -12592.0, 10760.0, -3906.0, -3190.0, -2114.0, -1968.0, 880.0, 883.0, -3583.0, -4262.0, -4495.0, 505.0, 2194.0, -469.0, -5780.0, 5805.0, -11440.0, -21706.0, 27385.0, -8533.0, 2782.0, 362.0, -5929.0, -1915.0, -4238.0, 1071.0, -8529.0, 2317.0, -7595.0, -5143.0, 240.0, 6792.0, -2586.0, 5445.0, -2862.0, -3263.0, -4361.0, 3596.0, -3985.0, -438.0, -1449.0, -2594.0, 627.0, -3802.0, 1196.0, -2165.0, 319.0, -4753.0, -5308.0, 3199.0, -3945.0, -2982.0, 850.0, -1623.0, -2724.0, -828.0, -3097.0, -6728.0, 4599.0, 1662.0, -6493.0, 2834.0, -35656.0, 20133.0, 12750.0, -7834.0, -1832.0, 172.0, -11288.0, 13703.0, -12787.0, -6303.0, -2303.0, -2038.0, -7853.0, 8006.0, 707.0, -811.0, 3311.0, -2042.0, -1985.0, -423.0, -2754.0, 335.0, -5464.0, 600.0, -3398.0, -866.0, -1193.0, -2135.0, -2609.0, 1194.0, -2424.0, -2590.0, -3526.0, 790.0, -5170.0, 5491.0, 51.0, -14384.0, 9287.0, -4215.0, -7155.0, 9432.0, -12910.0, -1309.0, 5215.0, -3607.0, -6808.0, 9298.0, -22541.0, -12006.0, 28921.0, -9387.0, -1677.0, -656.0, -4015.0, -998.0, -1964.0, -5664.0, -4743.0, -3378.0, -9891.0, 6259.0, -585.0, 3174.0, -315.0, -507.0, -132.0, -463.0, -2709.0, -1921.0, -2463.0, -2316.0, 455.0, -2531.0

这是FFT值：

850159, 149286, 265943, 245545, 268816, 273358, 259215, 258683, 247526, 273654, 242403, 281878, 307284, 278415, 271214, 258875, 253768, 252473, 255385, 220324, 231414, 242633, 226099, 191531, 248391, 171515, 218672, 186567, 214938, 224413, 216581, 235749, 186375, 164166, 44581, 278924, 93980, 175930, 178638, 154459, 170033, 192662, 140531, 132274, 128717, 119741, 260519, 78757, 246641, 188627, 160756, 119053, 131311, 98181, 100447, 111493, 168179, 130609, 95353, 186940, 109973, 110107, 97234, 140556, 196081, 214005, 135410, 35912, 141008, 138413, 52177, 175686, 129286, 90057, 164437, 186183, 188454, 219768, 101066, 182511, 147675, 20046, 328759, 143892, 75628, 127744, 111484, 255969, 211560, 3946, 82988, 207029, 98322, 130963, 168633, 122201, 38624, 340126, 168085, 115223, 37400, 94940, 85540, 108631, 51006, 197575, 146065, 51800, 239245, 67848, 263602, 69630, 78250, 125533, 164151, 215253, 147920, 208686, 64569, 229339, 93518, 260792, 39166, 125931, 242542, 48721, 174348, 141559, 125815, 78765, 79803, 270542, 135343, 89293, 167074, 111937, 130130, 23251, 220470, 144755, 83364, 59643, 263924, 81461, 146219, 101076, 98141, 100952, 145975, 170965, 107258, 24782, 164298, 133108, 153683, 96266, 184367, 252932, 66484, 150744, 140932, 48479, 196921, 85676, 117759, 220018, 87578, 204263, 406546, 205701, 153631, 329187, 232988, 75216, 88677, 77744, 201402, 237572, 39696, 254693, 423076, 393125, 318252, 98043, 212493, 70255, 3664, 148288, 81766, 31081, 173588, 262050, 240517, 72926, 194867, 166347, 41535, 163457, 90379, 27538, 87297, 161587, 182472, 36915, 262205, 199485, 215211, 87933, 59445, 76130, 66797, 263300, 108378, 205190, 221071, 272146, 213902, 125151, 171001, 44875, 107620, 118709, 32582, 17918, 91632, 166583, 131732, 270558, 152837, 146896, 61740, 39048, 180589, 208806, 163988, 130691, 186421, 88166, 331794, 293086, 188767, 104598, 61049, 66532, 92698, 172981, 51492, 144210, 96422, 146135, 143004, 337824, 130458, 91313, 137682, 112294, 263795, 112294, 137682, 91313, 130458, 337824, 143004, 146135, 96422, 144210, 51492, 172981, 92698, 66532, 61049, 104598, 188767, 293086, 331794, 88166, 186421, 130691, 163988, 208806, 180589, 39048, 61740, 146896, 152837, 270558, 131732, 166583, 91632, 17918, 32582, 118709, 107620, 44875, 171001, 125151, 213902, 272146, 221071, 205190, 108378, 263300, 66797, 76130, 59445, 87933, 215211, 199485, 262205, 36915, 182472, 161587, 87297, 27538, 90379, 163457, 41535, 166347, 194867, 72926, 240517, 262050, 173588, 31081, 81766, 148288, 3664, 70255, 212493, 98043, 318252, 393125, 423076, 254693, 39696, 237572, 201402, 77744, 88677, 75216, 232988, 329187, 153631, 205701, 406546, 204263, 87578, 220018, 117759, 85676, 196921, 48479, 140932, 150744, 66484, 252932, 184367, 96266, 153683, 133108, 164298, 24782, 107258, 170965, 145975, 100952, 98141, 101076, 146219, 81461, 263924, 59643, 83364, 144755, 220470, 23251, 130130, 111937, 167074, 89293, 135343, 270542, 79803, 78765, 125815, 141559, 174348, 48721, 242542, 125931, 39166, 260792, 93518, 229339, 64569, 208686, 147920, 215253, 164151, 125533, 78250, 69630, 263602, 67848, 239245, 51800, 146065, 197575, 51006, 108631, 85540, 94940, 37400, 115223, 168085, 340126, 38624, 122201, 168633, 130963, 98322, 207029, 82988, 3946, 211560, 255969, 111484, 127744, 75628, 143892, 328759, 20046, 147675, 182511, 101066, 219768, 188454, 186183, 164437, 90057, 129286, 175686, 52177, 138413, 141008, 35912, 135410, 214005, 196081, 140556, 97234, 110107, 109973, 186940, 95353, 130609, 168179, 111493, 100447, 98181, 131311, 119053, 160756, 188627, 246641, 78757, 260519, 119741, 128717, 132274, 140531, 192662, 170033, 154459, 178638, 175930, 93980, 278924, 44581, 164166, 186375, 235749, 216581, 224413, 214938, 186567, 218672, 171515, 248391, 191531, 226099, 242633, 231414, 220324, 255385, 252473, 253768, 258875, 271214, 278415, 307284, 281878, 242403, 273654, 247526, 258683, 259215, 273358, 268816, 245545, 265943

这些价值观仍然相去甚远。在我的另一只手腕上，我有一个单独的可穿戴设备，它跟踪我的心率，对于给定的样本，它报告的心率为77bpm。

更新3-使用Octive Online测试正常运行的FFT（稍后将在Octive中测试）。但是，不确定我是否正确处理数据。我会继续玩这个，看看我是否能提高结果。

这是频谱图：

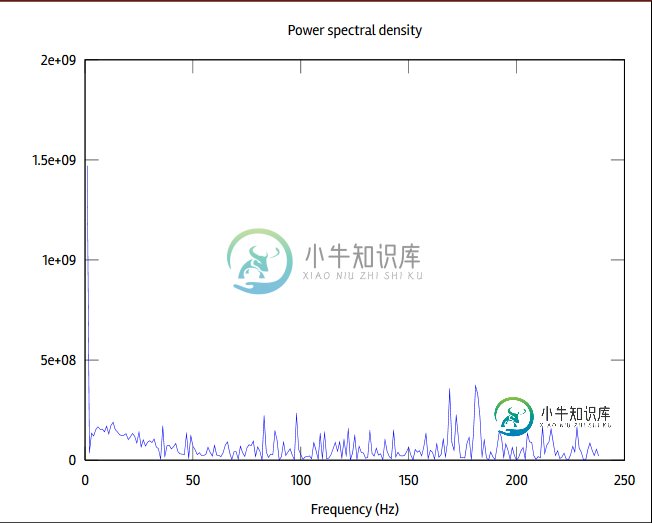
这是我的密码：

Fs = 50;                    % Sampling frequency
T = 1/Fs;                     % Sample time
L = 476;                     % Length of signal
t = (0:L-1)*T;                % Time vector
% Sum of a 50 Hz sinusoid and a 120 Hz sinusoid
y = [ -70756 -56465 -52389 -25199 -20352 -13660 -12615 -9202 -10225 -6168 -5338 4409 -1204 3009 1821 -3127 2076 720 675 -880 622 1851 -915 1296 -3069 -10 1114 2335 -4363 3386 -189 -2497 6326 -4007 -2708 1120 -2159 2643 -1817 749 6096 -2927 -1514 -24006 18897 10851 -2934 -1487 -1660 90 1999 -4448 2567 -1185 -2172 -4479 -253 5173 5956 2814 3279 1617 5174 -4152 911 2404 1579 792 573 -28 3251 159 -2170 727 2652 -2676 3039 -2938 2539 1586 -1447 132 -60 439 -87 -2239 2074 1268 -3559 1266 -18937 -869 25032 -6298 -1653 590 -1737 -3840 -484 -3408 -2470 -3663 -1526 -158 -748 5249 -44 1903 -1900 2513 -58 -2065 -450 -1131 -2262 3663 -2968 1262 -1687 -2745 -581 -11 -528 349 -2231 -1198 -2039 1362 -3671 580 -794 -3924 -1711 2093 -935 2423 -1017 -5674 -26830 27284 4433 -4604 -2655 -4541 -2643 2036 -3159 -3194 -2030 -2535 -5753 -31 5056 241 4452 -1591 -1056 573 -3637 -1224 -2728 3535 -2645 -1281 -1359 -1918 621 -2967 2535 -3048 -2820 -2530 -1202 315 -645 -3541 -3547 -2725 -4590 -124 620 -1866 -4450 -17536 4480 16119 -7421 2363 -8373 3109 -896 -6533 -1502 -378 -3602 -5893 -2730 2619 3532 675 -778 -590 288 -3793 -3934 -830 564 -1103 -5270 121 950 -2570 -502 -1556 -142 -1683 -2455 -3154 -2773 -2883 -1375 -2866 -5988 1914 -2311 -1654 -2757 -4321 -29329 26384 2636 -5619 -3352 -5555 -72 -5429 -751 -2445 -8749 -4021 -912 -2294 6468 135 1281 -2321 -320 -2578 -3737 -1470 -1841 -631 -1108 -2371 -2055 -3166 -1419 -677 -3666 -881 -20 -4403 1366 -3804 1064 -10377 4307 -3898 -845 3795 -7509 -21636 12672 9857 -2862 -4136 -1805 -5989 410 1048 -13174 -949 -3802 -4939 1437 -506 1305 6104 -1481 -3925 1949 -1001 -4920 -172 -1043 -1158 -2925 -994 -2615 720 -8393 3785 -3428 -7614 5963 -1540 -4688 -722 881 -4912 2058 -493 -7200 4413 -34168 29170 1335 -4874 -13611 8360 -4880 1229 -4077 -7090 4488 -8641 -3558 -2288 3415 -1972 4252 -578 -2509 -1106 -297 -3186 1630 -5392 261 -446 -12592 10760 -3906 -3190 -2114 -1968 880 883 -3583 -4262 -4495 505 2194 -469 -5780 5805 -11440 -21706 27385 -8533 2782 362 -5929 -1915 -4238 1071 -8529 2317 -7595 -5143 240 6792 -2586 5445 -2862 -3263 -4361 3596 -3985 -438 -1449 -2594 627 -3802 1196 -2165 319 -4753 -5308 3199 -3945 -2982 850 -1623 -2724 -828 -3097 -6728 4599 1662 -6493 2834 -35656 20133 12750 -7834 -1832 172 -11288 13703 -12787 -6303 -2303 -2038 -7853 8006 707 -811 3311 -2042 -1985 -423 -2754 335 -5464 600 -3398 -866 -1193 -2135 -2609 1194 -2424 -2590 -3526 790 -5170 5491 51 -14384 9287 -4215 -7155 9432 -12910 -1309 5215 -3607 -6808 9298 -22541 -12006 28921 -9387 -1677 -656 -4015 -998 -1964 -5664 -4743 -3378 -9891 6259 -585 3174 -315 -507 -132 -463 -2709 -1921 -2463 -2316 455 -2531.0 ] % Sinusoids plus noise

NFFT = 2^nextpow2(L); % Next power of 2 from length of y
Y = fft(y,NFFT);
Pyy = Y.*conj(Y)/L;


plot(Pyy(1:238))
title('Power spectral density')
xlabel('Frequency (Hz)')

更新4-决定尝试不同的方法。在这种情况下，使用自相关、低通滤波和FFT。

首先自动相关：如果数据中的噪声最小，结果相当准确。但是，一旦出现噪声，结果就不再可靠。这是代码：

private float correlate(List<Float> data, int nElements, int offset)
{
    float sum = 0;

    for(int i = 0; i < nElements - offset; i++)
    {
        sum += data.get(i) * data.get(i + offset);
    }
    return sum;
}

int getBeat(List<Float> data, int n)
{
    int minEle = 0, maxEle, i;
    float minVal, maxVal;

    List<Float> correlatedValues = new ArrayList<>();

    for(i = 0; i < n; i++)
    {
        correlatedValues.add(correlate(data, n, i));
    }

    minVal = correlatedValues.get(0);

    for(i = 1; i < n; i++)
    {
        if(correlatedValues.get(i) > correlatedValues.get(i - 1))
        {
            minVal = correlatedValues.get(i);
            minEle = i;
            break;
        }
    }

    maxVal = minVal;
    maxEle = minEle;
    for (i=minEle; i<n; i++)
    {
        if (correlatedValues.get(i) > maxVal)
        {
            maxVal = correlatedValues.get(i);
            maxEle = i;
        }
    }

    return maxEle;
}

返回的结果是拍之间的距离。将样本长度除以距离得到样本的心率。示例：470（样本量）/46（距离）=10（每10秒样本的拍数）*6=60Bpm。

如上所述，噪声掩盖了这一点，所以我试图根据这个例子拼凑出一个低通滤波器。这是我想出的代码：

private List<Float> lowPassFilter(List<Float> frequencies, float smoothing)
{
    float frequency = frequencies.get(0);
    for(int i  = 1; i < frequencies.size(); i++)
    {
        float currentFrequency = frequencies.get(i);
        frequency += (currentFrequency - frequency) / smoothing;
        frequencies.set(i, frequency);
    }
    return frequencies;
}

问题是，无论我通过什么运行低通滤波器的结果（自相关、肖维纳准则或通过峰值搜索），结果都是0（零）。我的猜测是过滤器的实现是关闭的。

然而，我也尝试使用FFT来获得频率，然后使用这些结果进行自动相关，结果仍然是0（零）。以下是使用FFT获取频率的代码：

    private List<Float> fft(List<Integer> ecgValues, TransformType transformType)
{
    int samplingFrequency = 50;

    List<Integer> transformedStream = new ArrayList<>();

    FastFourierTransformer ffs = new FastFourierTransformer(DftNormalization.STANDARD);
    double[] input = convertIntegerListToDoubleArray(ecgValues);

    Complex[] complex = ffs.transform(input, transformType);

    List<Float> magnitude = calculatePowerSpectrum(complex);

    List<Float> frequencies = powerSpectrumToFrequency(magnitude, samplingFrequency, ecgValues.size());

    return frequencies;
}

private List<Float> calculatePowerSpectrum(Complex[] complex)
{
    List<Float> magnitude = new ArrayList<>();

    for(int i = 0; i < complex.length - 1; i++)
    {
        double real = (complex[i].getReal());
        double imaginary = (complex[i].getImaginary());

        magnitude.add((float) Math.sqrt((real * real) + (imaginary * imaginary)));

    }

    return magnitude;
}

Answer 1

问得好。以下是解决问题的另一种方法：

您可以通过自动相关来检测信号中的周期元素。简而言之，可以通过将信号与自身的时移版本相乘来计算自相关，并存储乘积的总和。对所有可能的时移都这样做，你会得到自动相关。

自相关中的每个元素都告诉您，在不同的时间偏移下，信号与自身有多相似。如果信号中有周期性的东西（比如你的心跳），你会得到相关的峰值。

以下是第一个和第二个数据集的自相关（截断为前200个元素）：

请注意，所有自动相关都从第一个元素的一个微不足道的巨大峰值开始。这是因为信号与自身的非时移版本完全相关。这个峰值迅速下降。稍后，你会发现代表你心跳的峰值，两倍心跳，三倍心跳等等。

现在的任务非常简单：计算数据块的自相关性，跳过初始峰值并搜索最高峰值。它将被放置在信号周期性最强的地方。例如，您的心跳位置。

下面是一个C代码，它以暴力的方式实现了这一点（对不起，没有java）：

#include <stdio.h>
#include <stdint.h>
#include <stdlib.h>

static float timeseries1[] =
{
-59752, -66222, -45702, -34272, -25891, -19203, -13547, -12212, -5916, -8793, -5083, -2075, 3231, 6295, 4898, 3029, 3427, 2161, 4274, -1209, 3428, -1793, 2560, 5195, 1092, 8088, 7539, 6673, 7338, 8527, 11586, 12264, 7979, 4316, 8383, 3198, 2555, 3574, 753, 2964, -3042, 901, -3218, -6178, -21116, 24346, -602, -1520, -3454, -1430, -7914, -1906, -6920, -8216, -8013, -6836, -7863, -1031, 3049, -271, -1010, 1562, -166, -1069, 1143, 3268, -1074, -258, -749, 433, -450, 2612, -2582, 1063, -2656, 3751, -1608, 637, -997, -7, 1155, -556, -1397, 2807, -967, 2946, 1198, -1133, -11066, 5439, 11159, -1066, 643, -34, 441, 1378, 1451, -1664, -2054, -2390, -1484, -1227, 5589, 5151, 4068, 3040, -2243, 1762, -2942, 51, 1793, 245, 171, 639, -375, 1296, -1327, 729, -624, -2642, 3964, -2641, 286, -2766, -393, -316, 2343, -3658, -552, 613, 2687, -1347, 539, -11251, 2873, 14529, -5234, -919, -2486, -3641, 4647, 0, -2149, -4063, -2619, -749, 18, 5274, 6670, 1413, 2697, 2673, 157, -180, 166, 2352, 454, 2013, -2867, 3788, -423, 1680, 1167, -1282, 1554, 768, 298, 205, -480, 2618, 531, -839, -1067, -1056, 1693, 3300, 52, -2087, 259, -5031, -4896, 15720, -3576, -3005, 849, -2643, 2204, -4461, -1953, -572, -3743, -3664, -2254, 3326, 7791, 2388, -1847, 2592, -1142, -1550, 1224, -1044, -1698, -481, 1469, -479, -125, -1853, 455, -38, 167, -55, -2126, -2291, 96, 1179, -2948, -1960, -876, 29, -2660, 1465, -1025, -2131, 2058, -3111, -19865, 20644, 1786, -2853, -2190, -2047, -1873, -643, -921, -3191, -3524, -5160, -3216, 2431, 7117, 1796, 2435, -516, 1557, -1248, -2745, -860, -618, -565, -93, 602, -3364, -1658, 1398, -126, -1715, -1685, 680, -1805, 232, -2093, -1703, -2844, -628, -2049, -1450, 1737, -1216, 2681, -2963, -4605, -11062, 15109, 133, -3804, -2971, -1867, -194, -1433, -4328, -2887, -4452, -3241, -1997, 1815, 6139, 1655, 1583, 520, -2574, -2458, 299, -2345, -475, 991, -2273, -1038, -154, 267, -1528, -1720, -440, -77, -1717, -28, -2684, -606, -1862, -560, -2120, -900, -4206, 2636, -8, -917, -1249, -3586, -13119, 8999, 6520, -2474, -3229, -1804, -1933, -1104, -3035, -1307, -3457, -4996, -2804, -2841, 3889, 6843, 1992, -671, 548, -1871, -2000, 1441, -1519, -2303, -1067, 1131, -1001, -1396, -289, -968, 1864, -3006, -1918, -72, -239, -589, -2233, -1982, 2608, -2765, -1461, -2215, -1916, 2924, -13, 342, -446, -3427, -19378, 20846, 2310, -6999, -1806, -728, -932, -2081, -2129, -2054, -4103, -2641, -4826, 1457, 3338, 6764, 2363, -1811, 453, -2577, -796, -237, -663, -1594, -170, -922, -149, -2258, -816, -1250, -1640, 2522, -4363, 668, -3494, -557, -21, -263, -4197, 694, -2921, -161, -3000, -852, 3120, 339, -1138, -2066, -4505, -13751, 17435, -446, -4212, -1339, -2239, -223, -1322, -3550, -3987, -2102, -3505, -3971, 3695, 3535, 3150, 2459, 1575, -3297, -383, -1470, 1556, -2191, -123, -1444, -1572, 1973, -3773, 1206, -860, -1384, -395, -818, -934, -940, -494, 795, -1416, -3613, -442, 622, -2798, 1296, -373, -400, -1270, 278, -5536, -14798, 20071, -2973, -3795, -754, -3358, -393, -2279, -1834, -1983, -5568, -4118, -2595, 1443, 6367, 3245, 1500, -1697, 1287
};


static float timeseries2[] =
{
-35751, -32565, -28033, -23493, -18135, -10310, -8731, -4143, -5485, -2162, -955, -6393, -4211, -3047, -3097, -3232, -2975, -1571, -2105, -1440, -3880, -372, -227, -1266, -2269, -299, 2255, -2534, -3677, 675, 78, 415, -2274, -2256, 875, -13756, -5896, 15991, 585, -4356, 2706,
-2028, 2127, -2249, -1282, -2555, -2865, -2570, -2666, 3745, 5965, 2728, -73, 611, 342, 1297, 214, -1153, 496, -283, -1868, 1791, -541, 2044, -414, 1595, 72, -2262, -363, 1855, -649, 909, -815, -363, 2791, 152, 1072, -2025, 1291, -12311, -6729, 22739, -4036, -784, 2598, -871,
-2182, 1244, -2158, -2403, -1551, -3825, -4385, 4281, 5919, 6609, -2120, 480, 1070, -736, 525, -1520, -2225, 1795, 574, 781, -584, -1750, 175, 3339, -1175, 1186, -1319, 361, 885, -46, -1078, -2569, -720, 1533, 2465, 113, -1953, 2475, -5732, -22272, 24177, 235, 1385, -3850, 2291, -1417, -2452, -862, -3745, -932, -3586, -3987, -69, 5431, 3902, 2284, -619, 609, -1424, -1467, -1055, -1166, -1216, 1515, -1851,
-49, -4983, 1495, 3563, -873, -1933, -397, -933, 546, -1925, -753, -53, -2603, -591, 769, 3005, -2773, 2097, -5993, -21911, 23700, 3747, -4986, 595, -1815, -1589, -571, -2116, -1823, -6708, -1686, -1891, -991, 5178, 3719, 1188, -2394, 3992, -1555, -5306, 2830, 25, -2564, 2112, -1723, -3810, 4700, -2780, 520, -70, -2015, 1093, -2231, 2526,
-4651, -799, 764, -2429, 272, -564, 1119, -1089, 2371, -5627, -8118, 7574, 6499, -8635, 582, -2186, -1986, -477, -2178, -707, -6743, -3582,
-4409, 1806, 2718, 5820, -272, 1046, -580, -1552, -1184, -3206, -690, 1218, -871, -1919, -2552, 2127, -754, -1848, -3573, 3112, -1170, 468,
-2593, -382, -3280, 3664, -5572, 1992, -30, -7230, 8670, -2504, -4969, -14813, 225, 14109, 8194, -9438, -4781, 3102, -8626, 6428, -5387, -5050, 548, -10060, 6965, -2155, 2195, 5498, 359, -4090, 5130, -4214, 1478, -364, -6444, 5889, -3363, -1621, -3570, 8390, -5828, -1472, 841,
-8869, 11057, -6734, 173, 535, -638, -2628, -2751, 4754, 514, -2423, 1168, -3860, -23875, 18070, 7511, -3048, -1173, -6033, 5087, -5258,
-3012, -831, -1180, -5298, -557, -2993, 6236, 1417, 2683, 361, 2293, -4117, 1122, -1922, -3730, 2705, -848, -3560, 2100, -319, -495, -347, -2329, 1341, -805, 1227, -2463, -440, -1440, 1206, -2361, -411, -1481, 3837, -3101, 1851, -5779, -22183, 22335, 3443, -3854, -2077, -2311, 1471, -817, 792, -7227, -2963, -4038, -92, -1234, 4692, 3973, 2122, 1333, -222, -2997, 1279, -3531, 1335, 140, -375, -2235, 2795, 598,
-3233, -951, 1895, -288, -925, 1066, -3400, -1230, -2011, 2217, 1942, -1790, -1700, -1450, 756, -10710, -6744, 18590, -1435, -1739, -2097, -2638, -454, 67, -4556, -695, -5602, -2815, -2142, 764, 5958, 2175, 2055, -647, -466, -478, -1082, 527, -2214, 275, 274, -1687, -2358, 31, 1570, -1587, -871, -271, -2365, 1337, -831, -1095, -2056, -208, -1383, 2415, -1523, -1538, -719, -3842, -20933, 15223, 9978, -4030, -2521, 190, -4163, -2305, 1814, -2465, -4207, -3792, -2559, -2123, 2908, 5366, 2933, -1455, -57, 112, -2241, -1416, -2778, 2353, -1200, -2027,
-962, 1117, -1530, 157, -2902, 3466, -5072, 555, 1425, -2791, -1369, 156, -6789, 1961, -1111, 3631, -2592, -1643, 2039, -2865
};


float correlate (float * data, int nElements, int offset)
/////////////////////////////////////////////////////////
{
  float summ = 0;
  int i;

  for (i=0; i<nElements - offset; i++)
    summ += data[i] * data[(i+offset)];

  return summ;
}


int getBeat (float * data, int n)
/////////////////////////////////
{
  float * c = (float *) malloc (n * sizeof (float));

  int    minEle, maxEle, i;
  float  minVal, maxVal;

  // calculate the time-delayed correlation of the signal with itself:
  for (i=0; i<n; i++)
    c[i] = correlate (data, n, i);

  // Heuristic: Search for the first element that is higher than
  // it's precursor: (this is an heuristic to skip the trivial
  // correlation of the signal with itself).
  minVal = c[0];
  for (i=1; i<n; i++)
  {
    if (c[i] > c[i-1])
    {
      minVal = c[i];
      minEle = i;
      break;
    }
  }

  // Now just search for the highest peak. That's
  // where the highest periodicity in the signal is
  // located:
  maxVal = minVal;
  maxEle = minEle;
  for (i=minEle; i<n; i++)
  {
    if (c[i] > maxVal)
    {
      maxVal = c[i];
      maxEle = i;
    }
  }
  free (c);

  return maxEle;
}


int main (int argc, char **args)
{
  int nElements1 = sizeof (timeseries1) / sizeof (float);
  int nElements2 = sizeof (timeseries2) / sizeof (float);

  printf ("beat distance is %d samples\n",
    getBeat (timeseries1, nElements1));

  printf ("beat distance is %d samples\n",
    getBeat (timeseries2, nElements2));
  return 1;
}

找到的解决方案有：

beat distance is 46 samples
beat distance is 45 samples

我使用一种简单的启发式方法，通过从左到右搜索第一个相关性高于其前身的元素，跳过第一个索引。这通常在实践中效果很好。然而，如果你感兴趣的频率最高，你可以直接计算出需要忽略多少初始相关性。这同样适用于感兴趣的最低频率。

使用FFT可以更快地计算自相关，并且也可以通过零填充处理非二次幂（我稍后可能会添加这一点），但是对于演示来说，蛮力方法可能很好。

自相关方法的问题也应该被命名为：有可能两个或更多的心跳比一个心跳更相关。在这种情况下，你会得到一半的节拍频率或两倍的周期。如果进行恒定测量并检测到频率从一个测量值下降到另一个测量值，则不应该在相关性中查找绝对最大值，而是在预期频率附近搜索局部峰值。

注意，我没有对数据进行任何过滤。您可能可以通过应用窗口函数和使用一些数字滤波器消除噪声来改善结果。

为什么纯FFT解决方案可能失败：

您已经使用信号的FFT进行了一些实验，并寻找峰值，但您得到的结果并不太好。这是因为FFT将时域信号转换为正弦波分量。你的心跳看起来像正弦波吗？我不这么认为。它们是峰值，在基频中包含许多高频成分。事实上，你心跳的大部分能量都在高频段。这就是为什么你会在光谱中发现峰值。

因为拍的基频是你要找的，所以你得到的数据不适合直接的频域分析。除了自相关之外，你可能想看看倒谱。这是一种与FFT相关的变换，可以更好地处理高次谐波信号。

Answer 2

首先，让我们绘制你拥有的两个数据集。也许你一开始就应该这么做。

如果你想找到心率，你可能可以在时域或频域中确定结果。

要在时域中找到心率，您需要找到数据中的峰值。您的数据相当干净，因此您可以使用简单的峰值查找算法。搜索“时间序列查找峰值”会导致以下堆栈溢出问题：实时时间序列数据中的峰值信号检测

这篇文章提供了几个答案，你可以在一天内把它们拼凑起来。

正如你在最初的帖子中提到的，在10秒的样本中大约有10个峰值，因此在60秒内，心率将达到每分钟60次左右。

要在频域中查找心率，可以运行FFT。要正确运行FFT并找到频率箱，需要提供采样频率。我猜，由于在10秒内有500个样本，因此采样率必须为500个样本/10秒=50 Hz。

我没有在这台计算机上安装一个工作的Matlab或Octave，但是你可以自己运行它。例如，Mathworks有一个页面，显示运行FFT和绘制结果所需的所有代码：http://www.mathworks.com/help/matlab/ref/fft.html?refresh=true

该页面（非您的数据）的FFT图如下所示：

在上图中，您可以看到125Hz处的最高峰值。如果你使用你的数据，最高的单峰将是你的答案。

你显然不会运行Matlab为您的软件。然而，有很多开源FFT库可用。完成FFT后，您需要解析答案以找到最高峰。

无论你用什么方法来得到答案，你都需要将其与一些基本事实进行比较。我建议在智能手机（iPhone或Android）上使用心率应用程序。我使用的一个心率应用程序是安住弥的即时心率。此Stackoverflow问题涉及以下类型的应用程序：https://apple.stackexchange.com/questions/45176/how-accurate-are-ios-apps-that-measure-heart-rate

如果你需要更多的答案，我建议你在你的问题中添加“信号处理”标签，这样熟悉数字信号处理器的人就可以看到它。还有另一个拥有更多专家的StackExchange董事会（https://dsp.stackexchange.com/）。

当你找到你的解决方案时，请在这里发回你的结果。

2015年8月5日编辑

FFT的背景信息：

FFT是一种查找时域信号频率分量的算法。实际上，离散傅里叶变换（DFT）可以为您做到这一点。FFT只是DFT的快速实现（因此，快速傅立叶变换）。时域图中的重复频率将在频域中变得更加明显。例如，您的时域图每10秒显示10个强循环峰值。频域图将显示相同的数据，在10个峰值/10秒=1个/秒=1Hz处有一个大峰值。

这里有一些链接可以帮助您了解FFT的功能。我建议您安装Matlab或Octave（Matlab的免费开源版本）。

http://www.mathworks.com/help/matlab/examples/fft-for-spectral-analysis.html

http://www.dspguide.com/ch9/1.htm

这个链接特别显示了Matlab代码，从CSV文件中读取时间序列信号，然后绘制频谱图：

http://www.mathworks.com/matlabcentral/answers/155036-how-to-plot-fft-of-time-domain-data

必须提供采样频率（Fs是此变量的通用名称）。

Answer 3

首先，有趣的问题。绝对喜欢。

心跳的特征是压力下降，然后压力大幅上升，然后压力大幅下降，然后回到平均水平。

噪声比这更随机，并且在下降之前趋于平均（通常）。

通过比较移动噪声平均值和3个点上的最大变化，我们可以从噪声中过滤出实际的心跳。您可以在下面的JSfiddle中看到这一点：

不停摆弄

是的，我制作了圆形显示，因为我最初只是为了好玩而绘制它。当你使线条褪色时，它看起来很酷。另外，我知道这不是用java编写的，但是代码基本上是一样的。

无论如何，相关代码如下：

var averageSpike=0;
//itterate over data
for (var i = 0; i < data.length; i++) {
  //Calc moving average
  for (var l = 0; l < 10; l++) {
    var m = i - l;
    if (m < 0)
      m += data.length;
    if (m > data.length)
      m -= data.length;
    averageSpike += Math.abs(data[m]);
  }
  //4 times average is the threshhold for a heartbeat. This may require tweaking
  averageSpike /= 2.5;
  //Get 3 points ahead
  j = i + 1;
  k = i + 2;
  //wrap around array
  if (j > data.length - 1) {
    j = 0;
  }
  if (k > data.length - 1) {
    k = k - data.length;
  }
  var p1 = data[i];
  var p2 = data[j];
  var p3 = data[k];
  //Get min and max points
  //Notice that the min can only come from points 1 and 2, and the max from
  //  2 and 3. This is important as it filters out false positives.
  var min = Math.min(p1, p2);
  var max = Math.max(p2, p3);
  //Calc the difference
  var dif = max - min;
  //check if it is greater than the noise threshold
  if (dif >= averageSpike) {
    data2.push(dif);
  } else {
    data2.push(0);
  }
}

很明显，现在你有了一个峰值，你只需要记录它们，并取（在给定时间段内）有多少个峰值的移动平均值来计算bpm。

编辑：

我已经在这两个数据集上运行了一些测试。通过稍微调整移动平均线中的点数和除数，它们都可以达到100%的精度。但不是同时。在低噪声数据集上，如果噪声太低，就会出现误报。这可以通过限制噪声阈值的下限来解决。理想情况下，方程的渐近线为y=1，然后变为线性。。。但我还没有找到正确的方程式。

随着bpm的变化，也会出现问题。“噪声”数据点的数量将随着bpm的增加而减少，因此移动平均线中的点的数量将需要改变。这可以通过基于当前bpm修改循环计数和除数的简单反馈机制来解决。