使用动态规划选择最接近对的算法

Question

我一直在努力解决教授给我的这个问题，但没有找到合适的解决方案。问题如下

问题：矩形电路板有两个平行的侧面，它们之间的宽度为W。板的上侧有m个端子，n个端子（n

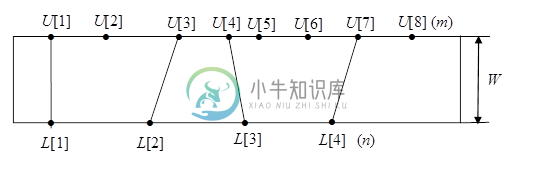
（a） 证明在最优解中，任意两条线段都不会相交。

（b） 设计一个O（mn）动态规划算法来解决这个最小化问题。您需要定义子问题，显示归纳公式、初始条件和伪代码。你可以用d（i，j）来表示U[i]和L[j]之间的距离，1≤ 我≤ m、 1个≤ j≤ n、 （d（i，j）=）的计算可以省略。

我的方法：

对于上述问题，我的方法是首先制作一个矩阵d（i， j），其中i是底部的端子，j是顶部的端子。d（i， j）具有与任何两个电路的所有距离。然后遍历每一行，我会找到最小的距离并标记相应的终端。但我不确定如果顶部电路都在一侧的最右边，这是否有效。所以有人能给我提供更好的方法吗？

Answer 1

我写了一个使用记忆的递归动态编程解决方案，复杂度为O（mn），在每个递归级别，我们可以选择将U[]数组中定义的当前点与L[]数组中定义的点连接起来，或者我们可以不这样做就前进：

#include<iostream>
#define INF 1e9

using namespace std;

int n, m, d[100][100], dp[100][100];

int solve(int idx1, int idx2){
    if(idx1 > m){
        if(idx2 < n) return INF;
        else return 0;
    }
    if(idx2 > n) return 0;
    if(dp[idx1][idx2] != -1) return dp[idx1][idx2];

    int v1, v2;

    //include current
    v1 = solve(idx1 + 1, idx2 + 1) + d[idx1][idx2];

    //do not include current
    v2 = solve(idx1 + 1, idx2);

    return dp[idx1][idx2] = min(v1, v2);
}

int main(){

    //enter the the distances

    for(int i = 0;i < 100;i++) for(int j = 0;j < 100;j++) dp[i][j] = -1;
    cout << solve(1, 1) << endl;
    return 0;
}

对于你问题的（a）部分，让我们假设2个线段确实相交，那么我们就不能有一个最优解，因为如果我们只是交换L[]数组定义的线段的2个endpoint，那么距离就会减少，因此给我们一个更好的解决方案。