如何使用树查找最长的公共子串？

Question

一组字符串的最长公共子字符串可以通过为字符串构建一个通用后缀树来找到，然后从其下方子树中的所有字符串中找到具有叶节点的最深内部节点

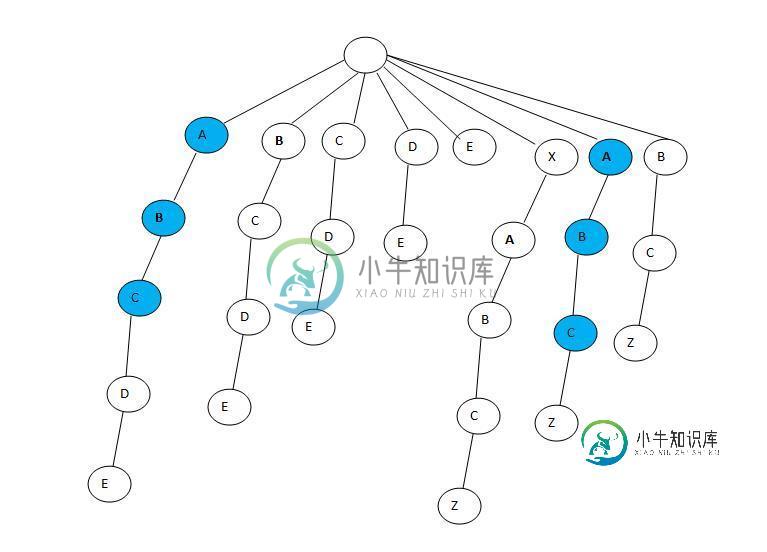
最长的公共子字符串是ABC，但它不是。我看不出wiki的描述在这里有什么帮助。
ABC不是最深的内部节点和叶节点。
有什么帮助来理解它是如何工作的吗？

Answer 1

您实际上还没有绘制后缀树。如果你做得好的话，从根本上说，你只会拥有每一个可能的角色一次。只有当一个字母可以有多个后缀时，树才会分裂。这会将树中的公共子字符串强制在一起，从而使它们可以查找。

Answer 2

就像以前说过的，你的树是不正确的。

这就是我在代码中运行“ABCDE$XABCZ”时得到的结果。

后缀树代码：

String = ABCDE$XABCZ$
End of word character 1 = $
└── (0)
    ├── (20) $
    ├── (22) ABC
    │   ├── (15) DE$
    │   └── (23) Z$
    ├── (24) BC
    │   ├── (16) DE$
    │   └── (25) Z$
    ├── (26) C
    │   ├── (17) DE$
    │   └── (27) Z$
    ├── (18) DE$
    ├── (19) E$
    ├── (21) XABCZ$
    └── (28) Z$

在（紧凑的）后缀树中，您需要找到最深的内部节点，这些节点包含所有字符串中的叶节点。如果在同一深度有多个节点，则必须比较该节点表示的字符串长度。i、 e.ABC、BC和C都有相同的深度，因此您必须比较ABC、BC和C字符串的长度，看看哪个更长；这显然是ABC。

后缀Trie代码：

└── null
    ├── A
    │   └── B
    │       └── C
    │           ├── D
    │           │   └── (E) ABCDE
    │           └── (Z) ABCZ
    ├── B
    │   └── C
    │       ├── D
    │       │   └── (E) BCDE
    │       └── (Z) BCZ
    ├── C
    │   ├── D
    │   │   └── (E) CDE
    │   └── (Z) CZ
    ├── D
    │   └── (E) DE
    ├── (E) E
    ├── X
    │   └── A
    │       └── B
    │           └── C
    │               └── (Z) XABCZ
    └── (Z) Z

在（非压缩）后缀trie中，查找包含所有字符串中叶节点的最深内部节点。

希望能有帮助。