有向图上的DFS
我很难理解Kosaraju寻找有向图的强连通成分的算法。以下是我笔记本上的内容(我是学生:D):
- 从任意顶点开始(用#1标记)并执行DFS。如果无法继续,请使用#2标记上次访问的顶点,然后启动另一个DFS(跳过已标记的顶点),依此类推。
- 变换图形的位置。
- 按相反顺序执行DFS从每个顶点开始,在每个DFS之后结束访问的顶点属于同一个SCC
我举了一个例子:
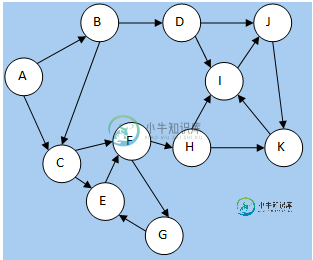
从E开始的第一步后,标签为:
- E
- G
- K
- J
- 我
- H
- F
- C
- D
- B
- A
那么问题来了:DFS在有向图和无向图中有区别吗?我在脑海中对第一步进行了心理测试,忽略了箭头(就像它是无方向的),只得到了正确的#1代表E(当然)和#2代表G,但是#3落在了J上,而不是K上。所以我想也许我应该尊重箭头,并考虑到这一点做了一个DFS,但是在从E开始的第一次传球之后,我不能从G(也就是#2)去任何地方,所以我被困在那里了。
关于有向图上的DFS有什么我不知道的吗?我只学过无向图!
共有1个答案
你的第二步是不完整的。见维基百科:
Kosaraju的算法工作原理如下:
- 设G是有向图,S是空堆栈。
- 而S不包含所有顶点:
- 选择一个不在S中的任意顶点v。每次深度优先搜索完成扩展顶点u时,将u推到S上。
- 从S弹出顶部顶点v。在转置图中从v开始执行深度优先搜索。访问的顶点集将给出包含v的强连通分量;记录并从图G和堆栈S中删除所有这些顶点。同样,可以使用宽度优先搜索(BFS)代替深度优先搜索
因此,您不应该只对最后一个顶点和第一个顶点执行某些操作,而应该对DFS中的每个顶点执行这些操作。
还要注意的是,你应该回溯-当你不能再往前走时,你就转到上一个顶点,然后从那里继续。
不,你不能把它当作一个无向图——边的方向很重要。
因此,从
E开始,你可以,例如,去F,然后G,然后回到F,然后H,然后K,然后I,然后回到I,K,H,F,最后是E,已将所有访问的顶点推到堆栈上。
-
我有一个无向图,我想从一个起始节点列出所有可能的路径。2个节点之间的每个连接在列出的路径中是唯一的,例如,给出以下图表示: 我无法使用现有的算法来完成它,我知道像DFS。任何帮助都将非常感谢。
-
我正在制作一个飞溅屏幕,我希望图像视图像悬浮一样不断上升然后下降。这将在数据库在后台加载时发生(AsyncTask)。我尝试过动画视图,但它只在一个方向上,而且只有一次。我如何完成这件事?提前谢谢你: D
-
在图论中,如果一个有向图从任意顶点出发无法经过若干条边回到该点,则这个图是一个有向无环图(DAG图)。 因为有向图中一个点经过两种路线到达另一个点未必形成环,因此有向无环图未必能转化成树,但任何有向树均为有向无环图。 一、简介 有向无环图是图论的重要概念,我们将首先介绍图的概念和定义,随后介绍有向图,再逐渐引至有向无环图(DAG)。值得一提的是,当DAG用于指代模型时一般指向贝叶斯网络。 一个图G
-
本文会围绕算法中DFS求有向图或无向图两点间所有路径,先讲解DFS以及有向图或无向图的意思。 有向图在图中的边是有方向的,表现出来就是有个箭头指示方向,节点只能单向通信或传递消息,相当于单行道,无向图边没方向是双向的,边连接的两个节点有通路可以双向通信,类似于双行道。 无向图,边没有方向的图称为无向图。邻接矩阵则是对称的,且只有0和1,因为没有方向的区别后,要么有边,要么没边。 DFS作为搜索算法
-
我有一个有向无环图,在该图中有一个原点。 我如何访问从可达的所有顶点,这样,如果我访问,我就已经访问了所有有的顶点了? 示例: 从开始,必须在之后访问。 我尝试只执行一个BFS并检查每个顶点的父级,如果没有访问它们,则稍后重新添加它,但这证明太慢了,我相信可以是。 知道图是二进制的可能会有帮助,每个顶点将被最多两个顶点指向。在另一个方向上,每个顶点指向很多顶点。

