连接所有岛屿的最低费用是多少?
有一个大小为N x M的网格,有些单元是岛,用“0”表示,其他的是水。每个水电池上都有一个数字,表示在该电池上做桥的成本。你必须找到所有岛屿都能连接起来的最小成本。如果一个单元格共享一条边或一个顶点,则该单元格与另一个单元格相连。
用什么算法可以解决这个问题?如果N,M的值很小,比如说NxM<=100,那么用什么作为蛮力方法呢?
示例:在给定的图像中,绿色单元格表示岛屿,蓝色单元格表示水,浅蓝色单元格表示应该在其上做桥的单元格。因此,对于下面的图像,答案将是17。

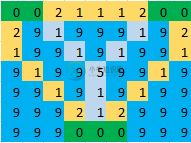
共有1个答案
为了解决这个问题,我将使用一个整数规划框架并定义三组决策变量:
- x_ij:表示是否在水上位置(i,j)建桥的二进制指示变量。
- y_ijbcn:一个二进制指示器,用于指示水位置(i,j)是否是连接b岛和C岛的第n个位置。
- l_bc:一个二进制指示变量,用于指示岛屿b和c是否直接链接(也就是您只能在桥格上行走,从b到c)。
对于建桥成本c_ij,最小化的目标值为sum_ij c_ij*x_ij。我们需要在模型中添加以下约束条件:
- 我们需要确保y_ijbcn变量有效。我们总是只有在那里建一座桥才能到达一个水广场,所以对于每个水位置(i,j)
y_ijbcn<=x_ij。此外,如果(i,j)不与岛B接壤,则y_ijbc1必须等于0。最后,对于n>1,只有在步骤n-1中使用了相邻水位置时,才能使用y_ijbcn。将N(i,j)定义为(i,j)相邻的水平方,这等价于y_ijbcn<=sum_{(l,m)in N(i,j)}y_lmbc(n-1)。 - 我们需要确保只有当b和c链接时才设置l_bc变量。如果我们将
i(c)定义为与岛c相邻的位置,则可以使用l_bc<=sum_{(i,j)in i(c),n}y_ijbcn来实现。 - 我们需要确保所有岛屿都是联系在一起的,要么是直接的,要么是间接的。这可以通过以下方式实现:对于每个岛的非空真子集S,要求S中至少有一个岛与S的补码中至少有一个岛相连,我们称之为S'。在约束中,我们可以通过为大小<=K/2(其中K是岛的数量)的每个非空集S添加一个约束来实现这一点,
sum_{b In S}sum_{c In S'}l_bc>=1
对于具有K个岛、W个水平方和指定最大路径长度N的问题实例,这是一个具有O(K^2wn)变量和O(K^2wn+2^K)约束的混合整数规划模型。显然,随着问题大小变大,这将变得难以解决,但对于您关心的大小,这可能是可以解决的。为了了解可伸缩性,我将使用pulp包在python中实现它。我们先从问题底部有3个岛屿的较小的7×9地图说起:
import itertools
import pulp
water = {(0, 2): 2.0, (0, 3): 1.0, (0, 4): 1.0, (0, 5): 1.0, (0, 6): 2.0,
(1, 0): 2.0, (1, 1): 9.0, (1, 2): 1.0, (1, 3): 9.0, (1, 4): 9.0,
(1, 5): 9.0, (1, 6): 1.0, (1, 7): 9.0, (1, 8): 2.0,
(2, 0): 1.0, (2, 1): 9.0, (2, 2): 9.0, (2, 3): 1.0, (2, 4): 9.0,
(2, 5): 1.0, (2, 6): 9.0, (2, 7): 9.0, (2, 8): 1.0,
(3, 0): 9.0, (3, 1): 1.0, (3, 2): 9.0, (3, 3): 9.0, (3, 4): 5.0,
(3, 5): 9.0, (3, 6): 9.0, (3, 7): 1.0, (3, 8): 9.0,
(4, 0): 9.0, (4, 1): 9.0, (4, 2): 1.0, (4, 3): 9.0, (4, 4): 1.0,
(4, 5): 9.0, (4, 6): 1.0, (4, 7): 9.0, (4, 8): 9.0,
(5, 0): 9.0, (5, 1): 9.0, (5, 2): 9.0, (5, 3): 2.0, (5, 4): 1.0,
(5, 5): 2.0, (5, 6): 9.0, (5, 7): 9.0, (5, 8): 9.0,
(6, 0): 9.0, (6, 1): 9.0, (6, 2): 9.0, (6, 6): 9.0, (6, 7): 9.0,
(6, 8): 9.0}
islands = {0: [(0, 0), (0, 1)], 1: [(0, 7), (0, 8)], 2: [(6, 3), (6, 4), (6, 5)]}
N = 6
# Island borders
iborders = {}
for k in islands:
iborders[k] = {}
for i, j in islands[k]:
for dx in [-1, 0, 1]:
for dy in [-1, 0, 1]:
if (i+dx, j+dy) in water:
iborders[k][(i+dx, j+dy)] = True
# Create models with specified variables
x = pulp.LpVariable.dicts("x", water.keys(), lowBound=0, upBound=1, cat=pulp.LpInteger)
pairs = [(b, c) for b in islands for c in islands if b < c]
yvals = []
for i, j in water:
for b, c in pairs:
for n in range(N):
yvals.append((i, j, b, c, n))
y = pulp.LpVariable.dicts("y", yvals, lowBound=0, upBound=1)
l = pulp.LpVariable.dicts("l", pairs, lowBound=0, upBound=1)
mod = pulp.LpProblem("Islands", pulp.LpMinimize)
# Objective
mod += sum([water[k] * x[k] for k in water])
# Valid y
for k in yvals:
i, j, b, c, n = k
mod += y[k] <= x[(i, j)]
if n == 0 and not (i, j) in iborders[b]:
mod += y[k] == 0
elif n > 0:
mod += y[k] <= sum([y[(i+dx, j+dy, b, c, n-1)] for dx in [-1, 0, 1] for dy in [-1, 0, 1] if (i+dx, j+dy) in water])
# Valid l
for b, c in pairs:
mod += l[(b, c)] <= sum([y[(i, j, B, C, n)] for i, j, B, C, n in yvals if (i, j) in iborders[c] and B==b and C==c])
# All islands connected (directly or indirectly)
ikeys = islands.keys()
for size in range(1, len(ikeys)/2+1):
for S in itertools.combinations(ikeys, size):
thisSubset = {m: True for m in S}
Sprime = [m for m in ikeys if not m in thisSubset]
mod += sum([l[(min(b, c), max(b, c))] for b in S for c in Sprime]) >= 1
# Solve and output
mod.solve()
for row in range(min([m[0] for m in water]), max([m[0] for m in water])+1):
for col in range(min([m[1] for m in water]), max([m[1] for m in water])+1):
if (row, col) in water:
if x[(row, col)].value() > 0.999:
print "B",
else:
print "-",
else:
print "I",
print ""
使用来自纸浆包的默认求解器(CBC求解器)运行并输出正确的解需要1.4秒:
I I - - - - - I I
- - B - - - B - -
- - - B - B - - -
- - - - B - - - -
- - - - B - - - -
- - - - B - - - -
- - - I I I - - -
接下来,考虑问题顶部的完整问题,这是一个13 x 14的网格,有7个岛:
water = {(i, j): 1.0 for i in range(13) for j in range(14)}
islands = {0: [(0, 0), (0, 1), (1, 0), (1, 1), (2, 0), (2, 1)],
1: [(9, 0), (9, 1), (10, 0), (10, 1), (10, 2), (11, 0), (11, 1),
(11, 2), (12, 0)],
2: [(0, 7), (0, 8), (1, 7), (1, 8), (2, 7)],
3: [(7, 7), (8, 6), (8, 7), (8, 8), (9, 7)],
4: [(0, 11), (0, 12), (0, 13), (1, 12)],
5: [(4, 10), (4, 11), (5, 10), (5, 11)],
6: [(11, 8), (11, 9), (11, 13), (12, 8), (12, 9), (12, 10), (12, 11),
(12, 12), (12, 13)]}
for k in islands:
for i, j in islands[k]:
del water[(i, j)]
for i, j in [(10, 7), (10, 8), (10, 9), (10, 10), (10, 11), (10, 12),
(11, 7), (12, 7)]:
water[(i, j)] = 20.0
N = 7
MIP求解者通常较快地得到好的解,然后花费大量的时间来证明解的最优性。使用与上面相同的求解器代码,程序不会在30分钟内完成。但是,您可以为求解器提供一个超时时间,以获得一个近似解:
mod.solve(pulp.solvers.PULP_CBC_CMD(maxSeconds=120))
I I - - - - - I I - - I I I
I I - - - - - I I - - - I -
I I - - - - - I - B - B - -
- - B - - - B - - - B - - -
- - - B - B - - - - I I - -
- - - - B - - - - - I I - -
- - - - - B - - - - - B - -
- - - - - B - I - - - - B -
- - - - B - I I I - - B - -
I I - B - - - I - - - - B -
I I I - - - - - - - - - - B
I I I - - - - - I I - - - I
I - - - - - - - I I I I I I
mod.solve(pulp.solvers.GUROBI(timeLimit=120))
这实际上找到了一个目标值为16的解,一个比OP能够用手找到的更好的解!
I I - - - - - I I - - I I I
I I - - - - - I I - - - I -
I I - - - - - I - B - B - -
- - B - - - - - - - B - - -
- - - B - - - - - - I I - -
- - - - B - - - - - I I - -
- - - - - B - - B B - - - -
- - - - - B - I - - B - - -
- - - - B - I I I - - B - -
I I - B - - - I - - - - B -
I I I - - - - - - - - - - B
I I I - - - - - I I - - - I
I - - - - - - - I I I I I I
-
我遇到了下面的问题 一排有N栋房子。每栋房子都可以漆成红色、绿色或蓝色。每种颜色给每间房子上色的成本是不同的。找到每栋房子的颜色,这样相邻的两栋房子就不会有相同的颜色,所有房子的着色总成本最低。 这是完整的问题 在我看来,这个问题有点令人困惑,因为目标是将成本降到最低,并确保相邻的房子没有相同的颜色。在这种情况下,我不应该从三种颜色中选择成本最低的两种颜色吗。 这里是颜色的成本 红色100美元 我
-
问题内容: 我已经仔细阅读了JSON描述http://json.org/,但是我不确定我是否知道简单问题的答案。最小可能的有效JSON是什么字符串? 字符串是有效的JSON吗? 简单数字是有效的JSON吗? 布尔值是有效的JSON吗? 空对象是有效的JSON吗? 空数组是有效的JSON吗? 问题答案: 在撰写本文时,JSON仅在RFC4627中进行了描述。它(在“2”开头)将JSON文本描述为序列
-
问题内容: 我有一张桌子,看起来像: 它是按组和日期排序的。我想要一个额外的列来显示每个组的 连续 颜色’R’的顺序号。 要求的输出: 我试图将窗口函数与按组和颜色列进行分区一起使用,但它返回的输出在下面是不正确的。 错误的查询和输出: 我想知道它是否可以在SQL中使用,还是应该切换到另一种语言(例如Python)? 问题答案: 这是使用窗口功能可以完成的方式。首先,我们创建一个CTE,该CTE具
-
我正在用木偶制作器生成一个PDF文件。它自动生成一个PDF-1.4文件。然后,我使用dss用PAdES签名对其进行数字签名。结果文件可以在PDF查看器中打开,PDFStudio似乎可以正确解析文档签名。 然而,这是否有效?维基百科声明PDF/A-2(基于1.7)增加了对PAdES的支持。我是否需要生成至少PDF-1.7(或PDF/A-2)才能拥有具有有效签名的有效PDF文件? 注意:我在技术术语和
-
我在尝试使用pandas软件包时遇到了这个问题。我已经使用命令安装了numpy 1.9.0和dateutil 2.5.0。我仍然看到这个错误。 是否有其他方法安装dateutil?而这只与熊猫包有关 回溯(最后一次调用):从pandas.compat.numpy import*文件“/Users/xyz/Library/Python/2.7/lib/Python/site packages/pan
-
问题内容: 问题 我有一个s 数组。对于那些不熟悉此类的人,重要的信息是它们提供了功能。 我想编写一个函数,该函数采用s的此数组,并将其分解为一组连接的矩形。 比方说,例如,这些是我的矩形(构造函数采用的参数,,,): 快速绘图显示A与B相交,B与C相交。D没有相交。一件乏味的ascii艺术作品也可以完成这项工作: 因此,我的函数的输出应为: 失败的代码 这是我解决问题的尝试: 不幸的是,这里似乎

