检查给定点是否在旋转元素的边界内

Question

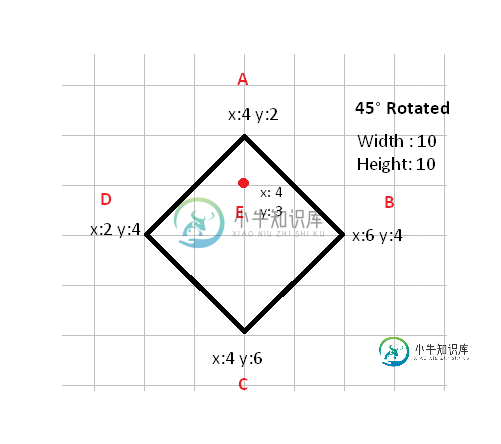
我有一个旋转45°的矩形，如下图所示，我有所有四个角的点，我需要找出给定点是否在旋转矩形的边界内。请注意，旋转将更改为任何数字，因此旋转需要成为公式的一部分。

所以我们有：

宽度：10

高度： 10

旋转角度：45度

旋转矩形的坐标：A B C D

给定坐标：E

感谢任何帮助。

Answer 1

你首先需要通过计算任意两个对角的平均坐标来得到矩形的中心。然后，您还需要获得矩形的两个维度，这可以通过确定具有最大y值的点以及具有最小和最大x值的两个点来实现。旋转前的水平尺寸是第一点和第二点之间的距离，旋转前的垂直尺寸是第一点和第三点之间的距离。

下一步是检查点E是否足够靠近矩形的中心，是否在其内部。最简单的方法是在旋转之前检查它的水平和垂直距离，如果它们小于或等于如果你擅长在边缘，则为相应尺寸的一半，那么它在矩形内部。您可以使用任何旋转角度的适当旋转矩阵获得旋转前的原始水平和垂直距离。

// center of rectangle
xO = (xA + xC) / 2;
yO = (yA + yC) / 2;
// point of largest y value
xPymax = xA;
yPymax = yA;
if (yB > yPymax)
{
    xPymax = xB;
    yPymax = yB;
}
if (yC > yPymax)
{
    xPymax = xC;
    yPymax = yC;
}
if (yD > yPymax)
{
    xPymax = xD;
    yPymax = yD;
}
// point of smallest x value
xPxmin = xA;
yPxmin = yA;
if (xB < xPxmin)
{
    xPxmin = xB;
    yPxmin = yB;
}
if (xC < xPxmin)
{
    xPxmin = xC;
    yPxmin = yC;
}
if (xD < xPxmin)
{
    xPxmin = xD;
    yPxmin = yD;
}
// point of largest x value
xPxmax = xA;
yPxmax = yA;
if (xB > xPxmax)
{
    xPxmax = xB;
    yPxmax = yB;
}
if (xC > xPxmax)
{
    xPxmax = xC;
    yPxmax = yC;
}
if (xD > xPxmax)
{
    xPxmax = xD;
    yPxmax = yD;
}
// dimensions of the rectangle
H = Math.sqrt((xPymax - xPxmin) * (xPymax - xPxmin) + (yPymax - yPxmin) * (yPymax - yPxmin));
V = Math.sqrt((xPymax - xPxmax) * (xPymax - xPxmax) + (yPymax - yPxmax) * (yPymax - yPxmax));
// calculating the original distances of point E from center
xdE = (xE - xO) * Math.cos(rot) + (yE - yO) * Math.sin(rot);
ydE = -(xE - xO) * Math.sin(rot) + (yE - yO) * Math.cos(rot);
// comparing to the dimentions of the rectangle
if (Math.abs(xdE) <= H / 2 && Math.abs(ydE) <= V / 2)  // this will consider a point on any edge as inside the rectangle, if you don't want this, just remove "="
    // the point is inside the rectangle
else
    // the point is outside the rectangle

Answer 2

任何多面体都可以表示为闭合半空间的有限交集。半空间由线性不等式给出，例如 x y 5

有关详细信息，请参阅任何关于凸性的书籍或维基百科链接：

https://en.wikipedia.org/wiki/Polytope#Properties https://en.wikipedia.org/wiki/Half-space_（几何）

Answer 3

假设没有矩形的变换矩阵。

如果有矩阵，则将该点乘以逆变换矩阵。然后，只需根据矩形顶部、左侧、右侧和底部的边界测试该点

考虑一个点沿顺时针方向旋转的凸多边形。

如果点在多边形的每条边（线）的左边，则点在该多边形内。

如果该点位于一条或多条边的右侧，则该点位于多边形的外部。

左边被定义为你的左边，好像站在线的起点，沿着它的长度看。或者看一个钟面，分针在3，然后分针的左边在4，右边在2。

要找出点在一条线的哪一边，你得到从线开始到结束的向量积，以及从线开始到点的向量积。如果向量积为正，则点在左边，如果零，则在线上，否则在右边。

const Point = (x, y) => ({x, y});
const Line = (p1, p2) => ({p1, p2});

function isPointLeft(l, p) { // l is line, p is point
    return 0 < (l.p2.x - l.p1.x) * (p.y - l.p1.y) - (l.p2.y - l.p1.y) * (p.x - l.p1.x);
}

因此，按顺时针顺序给出一组点，它们代表一个矩形，对照该点检查每个边。如果只剩下你在里面。

如果点在多边形内，函数返回true。假设多边形的点是顺时针顺序

function isPointInsidePoly(point, poly) {
    var i = 0;
    const line = Line(poly[poly.length - 1]);
    while (i < poly.length) {
         line.p2 = poly[i++];
         if (!isPointLeft(line, point)) { return false }
         line.p1 = line.p2;
    }
    return true;
}

简单演示创建一组点并旋转矩形。

绘制每个点。如果点在矩形内，则点绘制得稍大一点。

const Point = (x = 0, y = 0) => ({x, y});
const Line = (p1, p2) => ({p1, p2});
function isPointLeft(l, p) { // l is line, p is point
    return 0 < (l.p2.x - l.p1.x) * (p.y - l.p1.y) - (l.p2.y - l.p1.y) * (p.x - l.p1.x);
}
function isPointInsidePoly(point, poly) {
    var i = 0;
    const line = Line(poly[poly.length - 1]);
    while (i < poly.length) {
         line.p2 = poly[i++];
         if (!isPointLeft(line, point)) { return false }
         line.p1 = line.p2;
    }
    return true;
}


requestAnimationFrame(renderLoop);
const ctx = canvas.getContext("2d");
const [W, H] = [canvas.width, canvas.height];
const rand = (m, M) => Math.random() * (M - m) + m;
const setOf = (count, cb, i = 0, a = []) => {while (i < count) { a.push(cb(i++)) } return a}
function drawPoint(p, size) {
    ctx.strokeStyle = "#000";
    ctx.beginPath();
    ctx.arc(p.x, p.y, size, 0, Math.PI * 2);
    ctx.stroke();
}
const rect = {
    x: W / 2, y: H / 2,// x,y center of rectangle
    w: 80, h: 20,      // w h from center
    points: [Point(), Point(), Point(), Point()],
    update(angle) {
        const transform = (x, y, res) => {
            res.x = x * ax - y * ay + this.x;
            res.y = x * ay + y * ax + this.y;
        }
        const [ax, ay] = [Math.cos(angle), Math.sin(angle)];
        const p = this.points;
        transform( this.w,  this.h, p[0]);
        transform(-this.w,  this.h, p[1]);
        transform(-this.w, -this.h, p[2]);
        transform( this.w, -this.h, p[3]);  
    },
    draw(ctx) {
        ctx.lineWidth = 1;
        ctx.strokeStyle = "red";
        ctx.beginPath();
        for (const p of this.points) { ctx.lineTo(p.x, p.y) }
        ctx.closePath();
        ctx.stroke();
     }
}; 
const testPoints = setOf(20, () => Point(rand(20, W - 20), rand(20, H - 20)));
function renderLoop(time) {
    ctx.clearRect(0, 0, W, H);
    rect.update(time / 2300);
    rect.draw(ctx);
    for (const p of testPoints) {
        if (isPointInsidePoly(p, rect.points)) { drawPoint(p, 3) }
        drawPoint(p, 1);
    }
    requestAnimationFrame(renderLoop);
}

html lang-html prettyprint-override"><canvas id="canvas" width="200" height="200"></canvas>