给定一些AABB，找到包含它们的最小总表面积AABB？

Question

我有许多对象需要渲染到HTML5画布上。我的输入是轴对齐边界框的有序列表。这些框经常重叠，但也经常在它们之间留下大面积的空白。

我想尽量减少我必须创建的画布表面面积，以便以正确的顺序渲染所有这些项目，而不必在多个画布上渲染单个对象的部分（从而避免简单地创建紧贴所有占用空间的画布）。

所以基本上，我希望紧密的对象组都呈现在同一个画布上，而不重叠的对象应该呈现在单独的画布上。但是，并不是所有重叠的对象都应该呈现在单个画布上——例如，一个非常高、非常宽的对象稍微重叠形成一个L，仍然应该呈现在两个单独的画布上，因为将它们组合在一起会导致L的开放部分浪费很多画布空间。

维护 Z 顺序也会导致一些困难的情况。例如，下图表示一种潜在的排列方式：

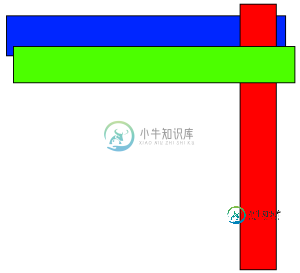
在这种情况下，您可能希望将蓝色和绿色图层合并到一个画布中，但是如果不包括红色图层，您就无法以这种方式产生正确的分层，并且您最终会有很多死空间。

但是你也不能只将组合图层限制在Z顺序连续的项目上。Z顺序可能与上图相同，但是红色项目可能碰巧与其他项目不重叠，在这种情况下，你确实想组合蓝色和绿色图层。

我在苦苦思索这个问题的好算法。有人想插话吗？

Answer 1

从AABBs的z排序数组开始，

>

将每个 AABB 添加到结果数组中，也按 z 顺序排序

一个。将这些要添加的 AAB 中的每一个与结果数组中已有的所有其他 AAB 进行比较

>

查看要添加的AABB和任何其他AABB的哪个组合会产生最小的额外表面积。（可能没有一个会，并且要添加的AABB不应该与任何其他组合。）

当合并会导致表面区域变小时，请检查相交问题(即，另一个AABB与另一个AABB重叠，并且与要添加的AABB重叠)

如果不存在这样的交叉问题，请记住另一个AABB，继续寻找更好的可能组合

湾。当最终找到最佳组合（或没有组合）时，将待添加的AABB添加到结果数组中

>

根据交叉点问题的存在，要添加的AABB可以与结果数组中的其他AABB组合并插入到其他AABB的位置

否则，组合或新AABB本身被添加到结果数组的顶部

对下一个 AABB 重复上述步骤

它不是一个很好的算法，也不能完美地完成所有事情。首先，当发现AABB的组合时，它不会试图找出是否也可以将第三或第四（或第五）个AABB添加到组合中以改进区域保护。

以下是此算法在 Java 脚本中的实现：

algorithm = function(allAABBsInSortedOrder) {
    var smallestCanvasSurfaceArea = [];

    goog.array.forEach(allAABBsInSortedOrder, function(aabb) {
        smallestCanvasSurfaceArea = findSmallestSurfaceArea(aabb, smallestCanvasSurfaceArea);
    })
};

findSmallestSurfaceArea = function(nextAABB, combinedAABBsInSortedOrder) {
    var nextAABBarea = areaOf(nextAABB);

    if (!nextAABB) {
        return combinedAABBsInSortedOrder;
    }

    var aabbToCombineWith = {'index': -1, 'area': nextAABBarea, 'upOrDown': 0};

    goog.array.forEach(combinedAABBsInSortedOrder, function(aabb, idx) {
        // Improvement - exhaustive combinations (three AABBs? Four?)
        if (areaOf(combine(aabb, nextAABB) - nextAABBarea <= aabbToCombineWith['area']) {
            var overlapLower = false;
            var overlapNext = false;

            goog.array.forEach(combinedAABBsInSortedOrder, function(intersectAABB, intersectIdx) {
                if (intersectIdx > idx) {
                    if (checkForIntersect(aabb, intersectAABB)) {
                        overlapLower = true;
                    }
                    if (checkForIntersect(nextAABB, intersectAABB)) {
                        overlapNext = true;
                    }
                }
            });

            if (overlapLower && !overlapNext) {
                aabbsToCombineWith['index'] = idx;
                aabbsToCombineWith['area'] = areaOf(aabb);
                aabbsToCombineWith['upOrDown'] = -1;
            }
            else if (!overlapLower && overlapNext) {
                aabbsToCombineWith['index'] = idx;
                aabbsToCombineWith['area'] = areaOf(aabb);
                aabbsToCombineWith['upOrDown'] = 1;
            }
            else if (!overlapLower && !overlapNext) {
                aabbsToCombineWith['index'] = idx;
                aabbsToCombineWith['area'] = areaOf(aabb);
                aabbsToCombineWith['upOrDown'] = 0;
            }
        }
    });

    if (aabbToCombineWith['index'] != -1) {
        var combinedAABB = combine(combinedAABBsInSortedOrder[aabbToCombineWith['index']], nextAABB);
        if (aabbToCombineWith['upOrDown'] == -1) {
            combinedAABBsInSortedOrder[aabbToCombineWith['index']] = combinedAABB;
        }
        else {
            combinedAABBsInSortedOrder.push(combinedAABB);
            combinedAABBsInSortedOrder.splice(aabbToConbineWith['index'], 1);
        }
    }
    else {
        combinedAABBsInSortedOrder.push(nextAABB);
    }

    return combinedAABBsInSortedOrder;
};

Answer 2

这里有一个简单的建议，它可能不会解决某些角落问题，但至少可以部分解决，并有望提出更好的解决方案：

a = <a z-ordered list of the objects> ;
b = [];
bounds = null;
objects = [];
while ( a.length > 0) {
    c = a.pop();
    if( <c overlaps bounds> && <area of combined canvases> < <area of seperate canvases> || bounds === null) {
         objects.push(c);
         bounds = <union of bounds and c, or bounds of c if bounds is null>;
     } else {
          b.push(c);
     }
     if( a.length === 0) {
          a = b;
          b = [];
          <do something with the current bounds and objects list>
          bounds = null;
          objects = [];
     }
}

在哪里

 < area of combined canvases> = sum( < area of each canvas> ) - sum( <interesections> )
 < area of seperate conavases> = sum( < area of each canvas> )

这不会捕捉到两个非相交对象都与一个公共对象相交的情况，但可以通过在每次迭代时回顾所有较低z顺序的对象来改进这种情况。

Answer 3

此问题在 3D 中众所周知，用于在光线追踪或碰撞检测中构建高性能 AABB 层次结构。尝试在谷歌上搜索“BVH”，“表面积启发式”和/或“SAH”。以下论文的3.1节具有良好的启发式算法;这应该很容易适应你的2D案例：http://graphics.stanford.edu/~boulos/papers/togbvh.pdf