我们必须创建一个所有节点都有3个子节点的树吗？

Question

构建哈夫曼树的步骤输入是唯一字符的数组及其出现频率，输出是哈夫曼树。

>

为每个唯一字符创建一个叶节点，并构建所有叶节点的最小堆（最小堆用作优先级队列。频率字段的值用于比较最小堆中的两个节点。最初，最不频繁的字符位于根）

从最小堆中以最小频率提取两个节点。

创建一个新的内部节点，其频率等于两个节点频率之和。将第一个提取的节点作为其左子节点，将另一个提取的节点作为其右子节点。将此节点添加到最小堆。

重复步骤#2和#3，直到堆只包含一个节点。剩下的节点是根节点，树是完整的。

在堆中，一个节点最多可以有2个子节点，对吗？

因此，如果我们想推广三元系统中编码字的哈夫曼算法（即使用符号0、1和2的编码字），我们可以做什么？我们必须创建一个所有节点都有3个子节点的树吗？

编辑：

我想是这样的。

构建哈夫曼树的步骤输入是唯一字符的数组及其出现频率，输出是哈夫曼树。

>

为每个唯一字符创建一个叶节点，并构建一个包含所有叶节点的最小堆

从最小堆中以最小频率提取三个节点。

创建一个新的内部节点，其频率等于三个节点频率之和。将第一个提取的节点作为其左子节点，第二个提取的节点作为其中间子节点，第三个提取的节点作为其右子节点。将此节点添加到最小堆。

重复步骤#2和#3，直到堆只包含一个节点。剩下的节点是根节点，树是完整的。

我们如何证明该算法产生最优三值码？

编辑2：假设频率为5,9,12,13,16,45。

它们的数目是偶数，因此我们添加了一个频率为0的虚拟节点。我们把它放在数组的末尾吗？那么，情况会是这样吗？

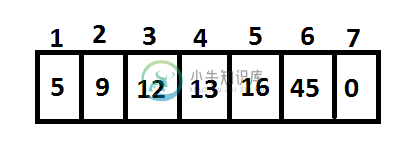
那么我们会有下面的堆吗？

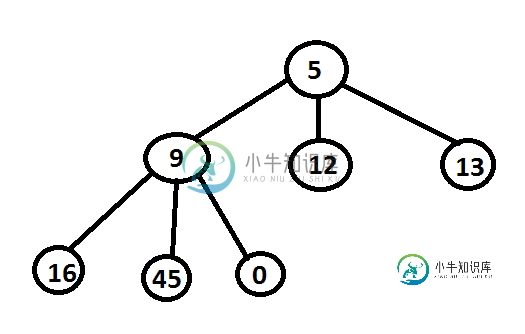
然后：

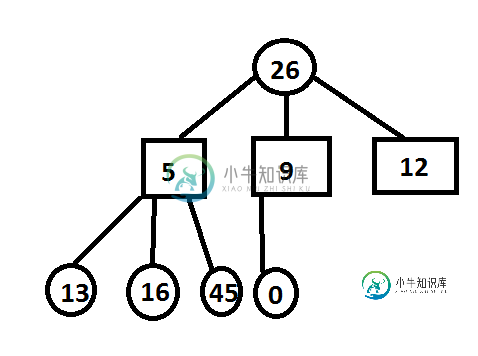
然后：

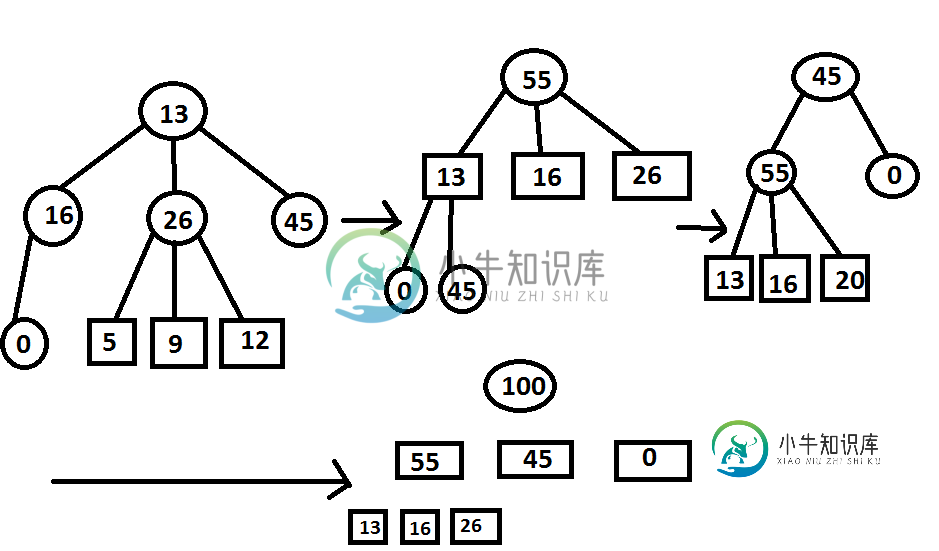
还是我理解错了？

Answer 1

对必须创建包含3个子节点的所有节点。为什么是3？您还可以使用具有n个子节点的节点进行n元哈夫曼编码。这棵树看起来像这样-（对于n=3）

    *
  / | \
 *  *  *
   /|\
  * * *

我给的算法是为了方便参考。

HUFFMAN_TERNARY(C)
{
   IF |C|=EVEN 
   THEN ADD DUMMY CHARACTER Z WITH FREQUENCY 0.

   N=|C|
   Q=C;  //WE ARE BASICALLY HEAPIFYING THE CHARACTERS

   FOR I=1 TO floor(N/2)
   {
     ALLOCATE NEW_NODE;
     LEFT[NEW_NODE]= U= EXTRACT_MIN(Q)
     MID[NEW_NODE] = V= EXTRACT_MIN(Q)
     RIGHT[NEW_NODE]=W= EXTRACT_MIN(Q)
     F[NEW_NODE]=F[U]+F[V]+F[W];
     INSERT(Q,NEW_NODE);
   }
   RETURN EXTRACT_MIN(Q);
  } //END-OF-ALGO

为什么要添加额外的节点？使节点数为奇数。为什么？）因为我们想摆脱for循环，在Q中只有一个节点。

为什么选择楼层（N/2） 首先我们取3个节点。然后将其替换为1个节点。有N-2个节点。之后，我们总是取3个节点（如果不可用，则取1个节点，由于虚拟节点，永远不可能得到2个节点）并替换为1。在每次迭代中，我们将其减少2个节点。这就是为什么我们使用术语floor（N/2）。

使用一些示例字符集在纸上自己检查。你会明白的。

我在这里引用了里维斯特科曼的“算法简介”。

证明：一步一步的数学证明太长，无法在这里发布，但它与书中给出的证明非常相似。

任何最优树在最低级别具有最低的三个频率。（我们必须证明这一点）。（使用矛盾）假设情况并非如此，那么我们可以将频率较高的叶子从最低级别与最低的三片叶子之一切换，并获得较低的平均长度。在没有任何一般性损失的情况下，我们可以假设所有三个最低频率都是同一节点的子节点。如果它们处于相同的水平，则无论频率在哪里，平均长度都不会改变）。它们只在码字的最后一位有所不同（一个是0、1或2）。

同样，作为二进制码字，我们必须收缩三个节点，并从中产生一个新字符，其频率=三个节点（字符）频率的总数。像二进制霍夫曼码一样，我们看到最优树的代价是三个符号收缩的树和收缩前有节点的消除子树的总和。由于已经证明子树必须存在于最终的最优树中，我们可以用收缩的新创建节点在树上进行优化。

>

假设字符集包含频率5,9,12,13,16,45。

现在N=6-

N=7和C中的freq0,5,9,12,13,16,45

现在使用min priority queue获取3个值<代码>0然后5然后9。

添加它们在优先级队列中插入freq=0 9 5的新字符。这样继续下去。

树就会这样

         100
        / | \
       /  |  \
      /   |   \
     39   16  45  step-3
   /  | \
  14  12 13  step-2
/ | \  
0 5 9   step-1

我现在将直接模拟科尔曼人的证据。

引理1.设C是一个字母表，其中属于C的每个字符d都有频率c.freq.设x、y和z是C中频率最低的三个字符。然后存在C的最优前缀码，其中x、y和z的码字具有相同的长度，仅在最后一位有所不同。

证明：

> P>首先考虑任意树T生成任意最优前缀码。

然后，我们将对其进行修改，以生成表示另一个最佳前缀的树，从而使字符x、y、z在最大深度处显示为同级节点。

如果我们可以构建这样一个树，那么x、y和z的码字将具有相同的长度，并且仅在最后一位有所不同。

证明--

• 设a，b，c是三个字符，它们是T中最大深度的兄弟叶。

• 在不丧失一般性的情况下，我们假设a.freq

在剩下的证明中，我们可以得到x.freq=a.freq或y.freq=b.freq或z.freq=c.freq。但是如果x.freq=b.freq或x.freq=c.freq或y.freq=c.freq，那么它们都是相同的。为什么？让我看看。假设x=y、 y=z、 x=z但z=c和x

 T1

     *                       |
   / | \                     |
  *  *  x                    +---d(x)
/ | \                        |
y *  z                           +---d(y) or d(z)
 /|\                         |
a b c                        +---d(a) or d(b) or d(c) actually d(a)=d(b)=d(c)

T2
     *              
   / | \
  *  *  a
/ | \
y *  z
 /|\
x b c               

T3

     *              
   / | \
  *  *  x
/ | \
b *  z
 /|\
x y c

T4
     *              
   / | \
  *  *  a
/ | \
b *  c
 /|\
x y z


In case of T1 costt1= x.freq*d(x)+ cost_of_other_nodes + y.freq*d(y) + z.freq*d(z) + d(a)*a.freq + b.freq*d(b) + c.freq*d(c)
In case of T2 costt2= x.freq*d(a)+ cost_of_other_nodes + y.freq*d(y) + z.freq*d(z) + d(x)*a.freq + b.freq*d(b) + c.freq*d(c)
       costt1-costt2= x.freq*[d(x)-d(a)]+0             +    0        +     0       + a.freq[d(a)-d(x)]+0       +    0
                    = (a.freq-x.freq)*(d(a)-d(x))
                    >= 0      
So costt1>=costt2.                    --->(1)

Similarly we can show costt2 >= costt3--->(2)

And                   costt3 >= costt4--->(3)

From (1),(2) and (3) we get 

costt1>=costt4.-->(4)

But T1 is optimal.

So costt1<=costt4 -->(5)

From (4) and (5) we get costt1=costt2.

SO, T4 is an optimal tree in which x,y,and z appears as sibling leaves at maximum depth, from which the lemma follows.

引理-2

设C是一个给定的字母表，其频率C.freq为属于C的每个字符C定义。设x、y、z是C中频率最小的三个字符。设C1为字母C，删除字符x和y，添加新字符z1，以便C1=C-{x，y，z}并集{z1}。将C1的f定义为C，除了z1。freq=x.freq y.freq z.freq。设T1为表示字母C1的最佳前缀代码的任意树。然后，通过将z的叶节点替换为具有x、y和z作为子节点的内部节点，从T1获得的树T表示字母C的最佳前缀代码。

证据：

看，我们正在从T1过渡-

     *                            *              
   / | \                        / | \
  *  *  *                      *  *  *
/ | \                           / | \
* *  *        ---->             * z1 *
 /|\                            
x y z                                          

对于属于（c-{x，y，z}）的c，dT（c）=dT1（c）。[对应于T和T1树的深度]

因此c.freq*dT（c）=c.freq*dT1（c）。

因为dT（x）=dT（y）=dT（z）=dT1（z1）1

So we have `x.freq*dT(x)+y.freq*dT(y)+z.freq*dT(z)=(x.freq+y.freq+z.freq)(dT1(z)+1)`
                                                  = `z1.freq*dT1(z1)+x.freq+y.freq+z.freq`
Adding both side the cost of other nodes which is same in both T and T1.
x.freq*dT(x)+y.freq*dT(y)+z.freq*dT(z)+cost_of_other_nodes= z1.freq*dT1(z1)+x.freq+y.freq+z.freq+cost_of_other_nodes

So costt=costt1+x.freq+y.freq+z.freq
or equivalently

  costt1=costt-x.freq-y.freq-z.freq ---->(1)

现在我们用矛盾来证明引理。

现在我们用矛盾来证明引理。假设T不代表C的最优前缀码，那么存在一个最优树T2，使得costt2

costt3 = costt2-x.freq-y.freq-z.freq
       <  costt-x.freq-y.freq-z.freq
       =  costt1  (From 1)

与T1表示C1的最佳前缀码的假设相矛盾。因此，T必须代表字母C的最佳前缀代码。

-Proved.

过程HUFFMAN生成一个最佳前缀代码。证明：引理1和引理2的直接引理。

注：术语来源于算法导论第三版Cormen Rivest