如何找到无向图中的所有多边形？

Question

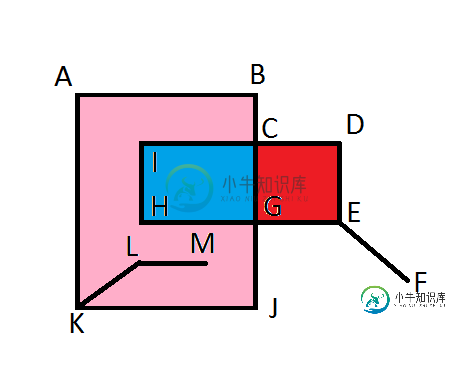
注意，有一个多边形ABCIHGJKLMLKA，它包括节点KLM，但多边形CDEG不包括F。

我读过关于这个问题的解决方案，但没有像我这样的leaf要求。在以前的解决方案中存在的一些公理是，每条边只使用两次，但是死端边总共需要遍历四次。也就是说，存在一个包含所有外部节点ABCDEFGJKLMLKA的多边形，但是它会被丢弃，因为它将朝外。

下面介绍了一种类似问题的解决方案，即sans the leafs：http://blog.reactoweb.com/2012/04/algorithm-101-finding-all-polygons-in-an-undirected-graph/

更新

链接的解决方案似乎无法按预期工作，下面举例说明：

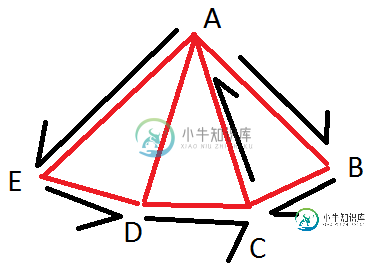
该算法将遍历图A-B-C-A-E-D-C，识别三角形ABC，也识别多边形CAEDC，这是不需要的

最新动态

实际上，这个问题有一个简单的解决方案：删除包含其他多边形点的较大多边形。

Answer 1

Re AndreyT建议使用DCEL：双连通边列表表示法的显著特征是，对于每个无向边，有两个列表节点，每个方向一个。我们将这些节点称为省道，并认为它们有一个头部和一个尾部。给定一个省道（例如，H-

多边形（通常称为面）可以通过查找排列的排列循环来找到，排列循环将每个省道按逆时针顺序映射到具有相同头部的下一个省道的反面。例如，如果我们从省道C开始-

C->D (E->D is next) D->E (G->E is next) E->G (C->G is next) G->C (D->C is next) C->D

恢复面部C-D-E-G-C以A-开头

A->B B->C C->I I->H H->G G->J J->K K->L L->M M->L L->K K->A A->B,

这就是A-B-C-I-H-G-J-K-L-M-L-K-A面。

这种方法需要一个连通图。（它将在断开的图上工作，但它可能不会给出您想要的结果。）它也会产生无限的面，你已经指出这是不可取的。要在无限面上找到一个镖（可以用来识别它），找到具有最小y坐标的顶点，通过最小x坐标打破联系。然后找到最后一个飞镖，它的头部以逆时针的顺序从光线向右直射。

Answer 2

step | description
1a   | while vertices with deg(v) = 0 exist
1b   |    mark vertices with deg(v) = 0 as leaf
     | 
2    | run algorithm on all vertices which are not marked as leaf
     | 
3a   | for each vertex marked as leaf 
3b   |    if vertex is inside a polygon
3c   |       check its edges // you have to decide what to do in which case
3d   |       adjust polygon

我将用你的例子来说明这一点：

step | result
1a   | find F and M
1b   |   mark F and M as leaf
1a   | find L
1b   |   mark L as leaf
1a   | find nothing: go to step 2
     |
2    | finds polygons: AKJGHICB (1), CIHG (2), and CGED (3)
     |
3a   | we have F, M, and L
3b   |   check F: 
     |     poly (1): cast ray: even result -> outside
     |     poly (2): cast ray: even result -> outside
     |     poly (3): cast ray: even result -> outside
     |     since F is always outside: no further action needed, unmark F
3b*  |   check M:
     |     poly (1): cast ray: odd result -> inside
     |     since M is inside a polygon: check how to add it
3c   |   check edge M-L:
     |     check if L is part of poly (1)
     |       if yes: add path to poly (1) (step 3d)
     |       if no: check if L is inside poly (1)
     |       -> no check L: odd result -> inside
     |         if inside: follow path, i.e. step 3c with edge L-K
     |         if outside: undefined behaviour
     |           -> inside
3c   |   check edge L-K:
     |     check if K is part of poly (1)
     |       -> yes: add path to poly
3d   |   Take poly (1) AKJGHICB
     |     replace K with KLK
     |     unmark K // note that K was never marked)
     |     remove K from path
     |     replace L with LML
     |     unmark L
     |     remove L from path
     |     unmark M // note that you should check if there are more
     |              // vertices to come for the replacement
     |     remove M from path 
     |   poly (1) is now AKLMLKJGHICB
3a   | we have no marked vertices left
     | finish


* note that in step 3b we could first have found L/checked L. Then it would be like this:

3b   |   check L:
     |     poly (1): cast ray: odd result -> inside
     |     since L is inside a polygon: check how to add it
3c   |   check L-K (or M-L, that would work as above and eventually try L-K)
     |     check if K is part of poly (1)
     |     if yes: add path to poly (1)
     |     -> yes
3d   |   Take poly (1) AKJGHICB
     |     replace K with KLK
     |     unmark K
     |     remove K from path
     |     unmark L
     |     remove L from path
     |   poly (1) is now AKLKJGHICB
3a   | we have M left // from now on a bit less detailed because it's the same again
3b   |   check M:
     |     poly (1): cast ray: odd result -> inside
     |   ...
3c   |   check M-L
     |     L is part of poly (1)
3d   |   replace L in the poly with LML and unmark L and M
     | finish

这应该是一个粗略的想法，你已经熟悉的算法应该如何工作。然而，它可能会有许多改进。