KISSFFT中2D阵列之间的逐元素乘法结果与SciPy FFT不同

Question

我正在与试验KISSFFT在 C ++
气馁使用后FFTPACK处理二维数组。

我编写了 逐个元素的乘法* 函数，将两个2D数组用转换后再相乘kiss_fftnd()。然后，通过逆FFT函数将乘法结果转换回去。不幸的是，我在
C语言 中从 kissfft 获得的结果与我在 python中 通过 SciPy 获得的结果不同，如下图所示：
*

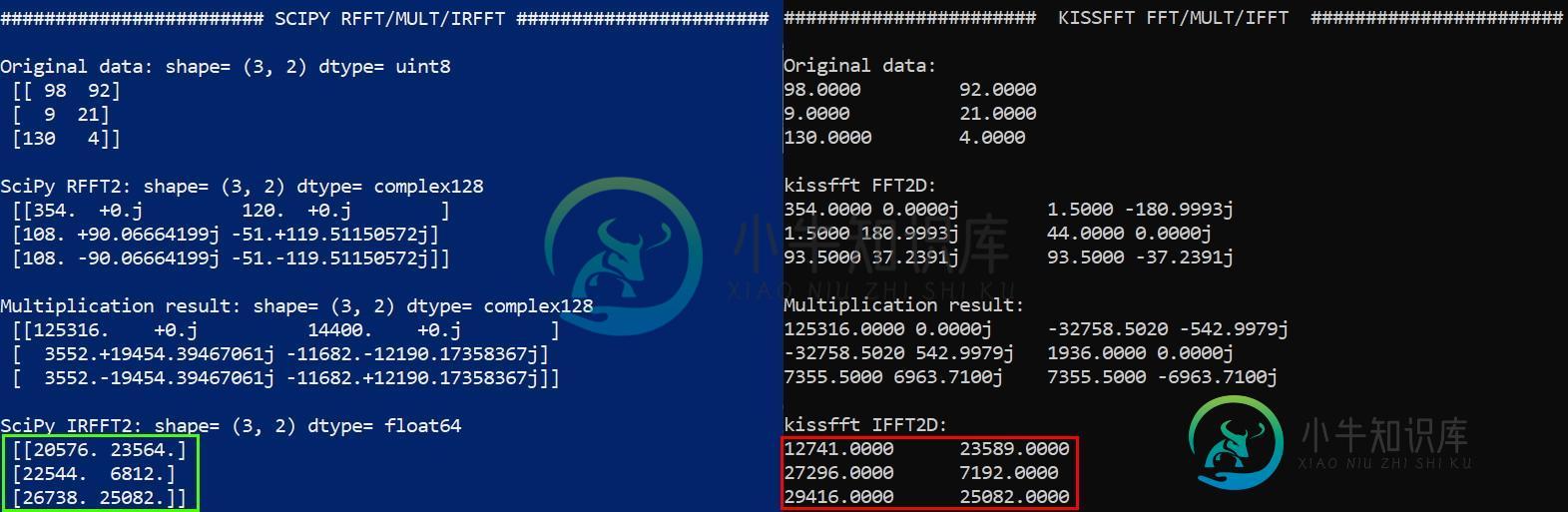
为了测试乘法函数，在转换2D输入数组后，为简单起见，我将其与自身相乘。这是Python的简化版本，用于说明算法：

import numpy as np
from scipy import fft as scipy_fft

in1 = np.array([[  98,  92], \
                [   9,  21], \
                [ 130,   4]], dtype=np.uint8)

fft_out = scipy_fft.rfft2(in1)
fft_mult = fft_out * fft_out
ifft_data = scipy_fft.irfft2(fft_mult, in1.shape)
print('\nSciPy IRFFT2: shape=', ifft_data.shape, 'dtype=', ifft_data.dtype, '\n', ifft_data)

我想不出用 kissfft
无法完成此简单操作的原因，这意味着我的乘法方法可能是错误的。由于的输出kiss_fftnd()是一维数组而不是2D数组，因此我用来对该数组进行迭代并执行逐元素乘法的逻辑可能不正确。

为什么这些结果不同？如何使Kissfft返回与SciPy相同的值？

如果您知道 kissfft 中已经正确执行乘法的函数， 那么 这对我也将起作用。请不要建议其他图书馆来完成这项工作。我正在寻找专门针对
kissfft 的答案。

这是Python中的完整源代码：

import numpy as np
from scipy import fft as scipy_fft

# complex_mult: multiplies two complex numbers
def complex_mult(n1, n2):
     real_part = n1.real*n2.real - n1.imag*n2.imag
     imag_part = n1.real*n2.imag + n2.real*n1.imag
     return complex(real_part, imag_part)

# fft2d_mult: multiplies two 2D arrays of complex numbers
def fft2d_mult(array1, array2):
    array_mult = np.empty(array1.shape, dtype=array1.dtype)
    h, w = in1.shape
    for j in range(h):
        for i in range(w):
            array_mult[j,i] = complex_mult(array1[j,i], array2[j,i])
    return array_mult


print("\n######################## SCIPY RFFT/MULT/IRFFT #######################\n");

# initialize input data
in1 = np.array([[  98,  92], \
                [   9,  21], \
                [ 130,   4]], dtype=np.uint8)

print('Original data: shape=', in1.shape, 'dtype=', in1.dtype, '\n', in1)

# perform 2D RFFT
fft_out = scipy_fft.rfft2(in1)
print('\nSciPy RFFT2: shape=', fft_out.shape, 'dtype=', fft_out.dtype, '\n', fft_out)

# perform element-wise multiplication
fft_mult = fft2d_mult(fft_out, fft_out) # equivalent to: fft_mult = fft_out * fft_out
print('\nMultiplication result: shape=', fft_mult.shape, 'dtype=', fft_mult.dtype, '\n', fft_mult)

# perform inverse 2D RFFT
ifft_data = scipy_fft.irfft2(fft_mult, in1.shape)
print('\nSciPy IRFFT2: shape=', ifft_data.shape, 'dtype=', ifft_data.dtype, '\n', ifft_data)

这是C ++中的完整源代码：

// compile with: g++ so_issue.cpp -o so_issue -I kissfft kissfft/kiss_fft.c kissfft/tools/kiss_fftnd.c
#include "kissfft/kiss_fft.h"
#include "kissfft/tools/kiss_fftnd.h"

// fft2d: receives a 2D array of floats, performs the forward transform with kiss_fftnd() and converts it into a kiss_fft_cpx array
kiss_fft_cpx* fft2d(float* input, int width, int height)
{
    const int numDim = 2;
    int shape[numDim] = { width, height };
    int nfft = width * height;

    // allocate 2D input array for FFT
    kiss_fft_cpx* cin = new kiss_fft_cpx[nfft];
    memset(cin, 0, nfft * sizeof(kiss_fft_cpx));

    // allocate 2D output array for FFT
    kiss_fft_cpx* cout = new kiss_fft_cpx[nfft];
    memset(cout, 0, nfft * sizeof(kiss_fft_cpx));

    // copy the input data to cin
    int k = 0;
    int idx = 0;
    for (int j = 0; j < height; ++j)
    {
        for (int i = 0; i < width; ++i)
        {
            idx = i + width * j; // access 1D array as 2D
            cin[k++].r = input[idx];
        }
    }

    // execute 2D FFT
    bool inverse_fft = false;
    kiss_fftnd_cfg cfg_f = kiss_fftnd_alloc(shape, numDim, inverse_fft, 0, 0);
    kiss_fftnd(cfg_f, cin , cout);

    // release resources
    kiss_fft_free(cfg_f);
    delete[] cin;

    return cout;
}

// fft2d: receives an array of kiss_fft_cpx elements, performs the inverse transform with kiss_fftnd() and returns the result in a new kiss_fft_cpx array
kiss_fft_cpx* ifft2d(kiss_fft_cpx* input, int width, int height)
{
    const int numDim = 2;
    int shape[numDim] = { width, height };
    int nfft = width * height;

    // allocate 2D output array for FFT
    kiss_fft_cpx* cout = new kiss_fft_cpx[nfft];
    memset(cout, 0, nfft * sizeof(kiss_fft_cpx));

    // execute inverse 2D FFT
    bool inverse_fft = true;
    kiss_fftnd_cfg cfg_i = kiss_fftnd_alloc(shape, numDim, inverse_fft, 0, 0);
    kiss_fftnd(cfg_i, input , cout);

    // release resources
    kiss_fft_free(cfg_i);

    return cout;
}

// complex_mult: performs element-wise multiplication between two complex numbers
kiss_fft_cpx complex_mult(const kiss_fft_cpx& a, const kiss_fft_cpx& b)
{
    kiss_fft_cpx c;

    // real_part = a.real*b.real - a.imag*b.imag
    c.r = a.r*b.r - a.i*b.i;

    // imag_part = a.real*b.imag + b.real*a.imag
    c.i = a.r*b.i + b.r*a.i;

    return c;
}

// complex_mult: performs element-wise multiplication between two kiss_fft_cpx arrays
kiss_fft_cpx* fft2d_mult(kiss_fft_cpx* input1, kiss_fft_cpx* input2, int width, int height)
{
    int nfft = width * height;
    kiss_fft_cpx* output = new kiss_fft_cpx[nfft];
    memset(output, 0, nfft * sizeof(kiss_fft_cpx));

    int idx = 0;
    for (int j = 0; j < height; ++j)
    {
        for (int i = 0; i < width; ++i)
        {
            idx = i + width * j; // access 1D array as 2D
            output[idx] = complex_mult(input1[idx], input2[idx]);
        }
    }

    return output;
}

void run_test(float* in1, const int& w, const int& h)
{
printf("\n#######################  KISSFFT FFT/MULT/IFFT  #######################\n\n");

    printf("Original data:\n");
    int idx = 0;
    for (int j = 0; j < h; ++j)
    {
        for (int i = 0; i < w; ++i)
        {
            idx = i + w * j;
            printf("%.4f  \t", in1[idx]);
        }
        printf("\n");
    }

    /* perform FFT */

    kiss_fft_cpx* cout = fft2d((float*)in1, w, h);

    printf("\nkissfft FFT2D:\n");
    for (int j = 0; j < h; ++j)
    {
        for (int i = 0; i < w; ++i)
        {
            idx = i + w * j;
            printf("%.4f %.4fj  \t", cout[idx].r,  cout[idx].i);
        }
        printf("\n");
    }

    /* perform element-wise multiplication */

    kiss_fft_cpx* cout_mult = fft2d_mult(cout, cout, w, h);

    printf("\nMultiplication result:\n");
    for (int j = 0; j < h; ++j)
    {
        for (int i = 0; i < w; ++i)
        {
            idx = i + w * j;
            printf("%.4f %.4fj  \t", cout_mult[idx].r,  cout_mult[idx].i);
        }
        printf("\n");
    }

    /* perform inverse FFT */

    kiss_fft_cpx* cinput = ifft2d(cout_mult, w, h);

    printf("\nkissfft IFFT2D:\n");

    int nfft = w * h;
    for (int j = 0; j < h; ++j)
    {
        for (int i = 0; i < w; ++i)
        {
            idx = i + w * j;
            printf("%.4f  \t", cinput[idx].r / nfft); // div by N to scale data back to the original range
        }
        printf("\n");
    }

    // release resources
    delete[] cout_mult;
    delete[] cinput;
    delete[] cout;
}

int main()
{
    int h = 3,  w = 2;
    float in1[h][w] =
    {
        {  98,  92 },
        {   9,  21 },
        { 130,  4  }
    };

    run_test((float*)in1, w, h);

    return 0;
}

Answer 1

问题是width和height中使用的顺序shape。此变量随后kiss_fftnd_alloc()作为参数传递给，height必须首先定义：

const int numDim = 2;
int shape[numDim] = { height, width };

使得在此之后改变内部fft2d()和ifft2d()应用程序中显示正确的结果。