如何解决RNN梯度消失和弥散的情况?
为了解决梯度爆炸问题,Thomas Mikolov首先提出了一个简单的启发性的解决方案,就是当梯度大于一定阈值的的时候,将它截断为一个较小的数。具体如算法1所述: 算法:当梯度爆炸时截断梯度(伪代码)
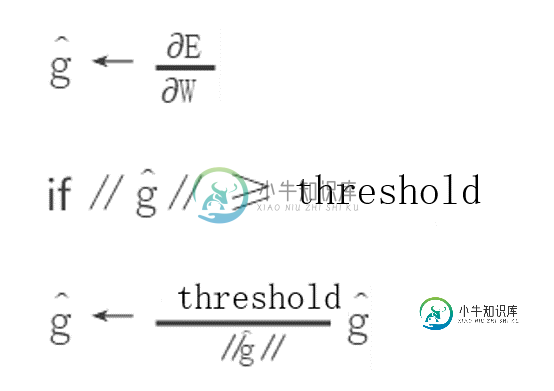
下图可视化了梯度截断的效果。它展示了一个小的rnn(其中W为权值矩阵,b为bias项)的决策面。这个模型是一个一小段时间的rnn单元组成;实心箭头表明每步梯度下降的训练过程。当梯度下降过程中,模型的目标函数取得了较高的误差时,梯度将被送到远离决策面的位置。截断模型产生了一个虚线,它将误差梯度拉回到离原始梯度接近的位置。
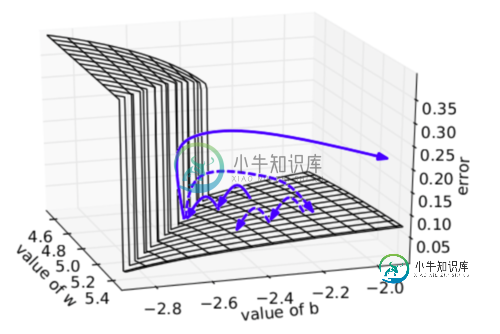
梯度爆炸,梯度截断可视化 为了解决梯度弥散的问题,我们介绍了两种方法。第一种方法是将随机初始化改为一个有关联的矩阵初始化。第二种方法是使用ReLU(Rectified Linear Units)代替sigmoid函数。ReLU的导数不是0就是1.因此,神经元的梯度将始终为1,而不会当梯度传播了一定时间之后变小。
-
本文向大家介绍如何解决RNN梯度爆炸和弥散的问题?相关面试题,主要包含被问及如何解决RNN梯度爆炸和弥散的问题?时的应答技巧和注意事项,需要的朋友参考一下 答:梯度爆炸:为解决梯度爆炸问题,Thomas Mikolov首先提出了一个简单的启发性的解决方案,就是当梯度大于一定阀值的时候,将它截断为一个较为小的数。 解决梯度弥散问题的两种方法: 第一种:将随机初始化W改为一个有关联的矩阵初始化。 第二
-
本文向大家介绍RNN容易梯度消失,怎么解决?相关面试题,主要包含被问及RNN容易梯度消失,怎么解决?时的应答技巧和注意事项,需要的朋友参考一下 参考回答: 1)、梯度裁剪(Clipping Gradient) 既然在BP过程中会产生梯度消失(就是偏导无限接近0,导致长时记忆无法更新),那么最简单粗暴的方法,设定阈值,当梯度小于阈值时,更新的梯度为阈值。 优点:简单粗暴 缺点:很难找到满意的阈值 2
-
本文向大家介绍如何解决梯度消失和梯度膨胀?相关面试题,主要包含被问及如何解决梯度消失和梯度膨胀?时的应答技巧和注意事项,需要的朋友参考一下 答: (1) 梯度消失:根据链式法则,如果每一层神经元对上一层的输出的偏导乘上权重解雇小于1的话,那么即使这个结果是0.99,经过足够多层传播之后,误差对输入层的偏导会趋于0; (2) 梯度膨胀:根据链式法则,如果每一层神经元对上一层的输出的偏导乘上权重结果都
-
本文向大家介绍如何解决梯度消失和梯度爆炸?相关面试题,主要包含被问及如何解决梯度消失和梯度爆炸?时的应答技巧和注意事项,需要的朋友参考一下 (1)梯度消失: 根据链式法则,如果每一层神经元对上一层的输出的偏导乘上权重结果都小于1的话,那么即使这个结果是0.99,在经过足够多层传播之后,误差对输入层的偏导会趋于0 可以采用ReLU激活函数有效的解决梯度消失的情况,也可以用Batch Normaliz
-
本文向大家介绍如何解决梯度消失和梯度膨胀?相关面试题,主要包含被问及如何解决梯度消失和梯度膨胀?时的应答技巧和注意事项,需要的朋友参考一下 梯度消失:根据链式法则,当每一层神经元对上一层的输出的偏导乘上权重结果都小于1的话,那么即使这个结果是0.99,经过多层传播之后,误差的输入层的偏导会趋于0,可以用relu激活函数来解决,因为relu=max(0,X),偏导数为1,不会造成梯度消失,而弊端是有
-
本文向大家介绍梯度消失梯度爆炸怎么解决相关面试题,主要包含被问及梯度消失梯度爆炸怎么解决时的应答技巧和注意事项,需要的朋友参考一下 参考回答: 1)、使用 ReLU、LReLU、ELU、maxout 等激活函数 sigmoid函数的梯度随着x的增大或减小和消失,而ReLU不会。 2)、使用批规范化 通过规范化操作将输出信号x规范化到均值为0,方差为1保证网络的稳定性。从上述分析分可以看到,反向传播

