字典火车路线的最佳数据结构？

Question

因此，我的任务是从本质上读取一个文件（记事本文件），该文件具有许多火车停靠站以及从一个停靠站到另一个停靠站所花费的时间。例如，它看起来像：

Stop A     15
Stop B     12
Stop C     9

现在，我需要返回并访问这些站点及其时间。我当时正在考虑读取文件并将其存储为字典。我的问题是，最好的字典是吗？还是有其他一些Python工具会被证明更有用？任何想法将不胜感激！

Answer 1

我会反驳说-直截了当的命令并不是最好的选择。

假设您有100个站点，并且有多条非字母和非数字的路线。想想巴黎地铁：

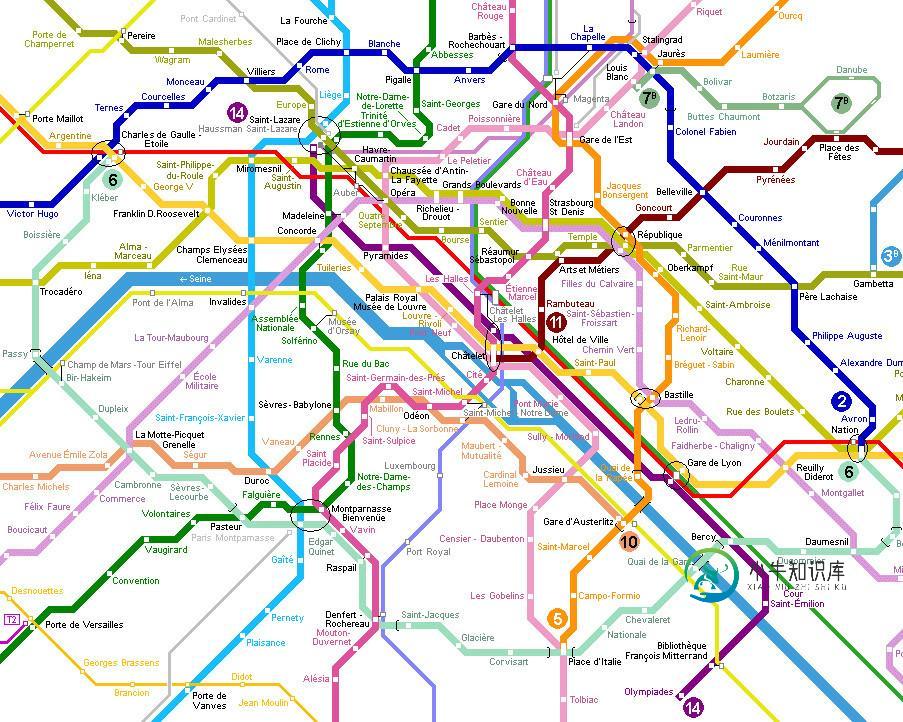
现在尝试使用直接的Python字典来计算FDR和La Fourche之间的时间吗？这涉及两个或多个不同的路线和多个选项。

甲树或某种形式的图形是较好的结构。字典对于1对1映射而言是极好的。树对于相互关联的节点的丰富描述更好。然后，您将使用类似Dijkstra的算法的导航方式。

由于嵌套的dict或list的dict是一个图，因此很容易提出一个递归示例：

def find_all_paths(graph, start, end, path=[]):
        path = path + [start]
        if start == end:
            return [path]
        if start not in graph:
            return []
        paths = []
        for node in graph[start]:
            if node not in path:
                newpaths = find_all_paths(graph, node, end, path)
                for newpath in newpaths:
                    paths.append(newpath)
        return paths

def min_path(graph, start, end):
    paths=find_all_paths(graph,start,end)
    mt=10**99
    mpath=[]
    print '\tAll paths:',paths
    for path in paths:
        t=sum(graph[i][j] for i,j in zip(path,path[1::]))
        print '\t\tevaluating:',path, t
        if t<mt: 
            mt=t
            mpath=path

    e1=' '.join('{}->{}:{}'.format(i,j,graph[i][j]) for i,j in zip(mpath,mpath[1::]))
    e2=str(sum(graph[i][j] for i,j in zip(mpath,mpath[1::])))
    print 'Best path: '+e1+'   Total: '+e2+'\n'

if __name__ == "__main__":
    graph = {'A': {'B':5, 'C':4},
             'B': {'C':3, 'D':10},
             'C': {'D':12},
             'D': {'C':5, 'E':9},
             'E': {'F':8},
             'F': {'C':7}}
    min_path(graph,'A','E')
    min_path(graph,'A','D')
    min_path(graph,'A','F')

印刷品：

    All paths: [['A', 'C', 'D', 'E'], ['A', 'B', 'C', 'D', 'E'], ['A', 'B', 'D', 'E']]
        evaluating: ['A', 'C', 'D', 'E'] 25
        evaluating: ['A', 'B', 'C', 'D', 'E'] 29
        evaluating: ['A', 'B', 'D', 'E'] 24
Best path: A->B:5 B->D:10 D->E:9   Total: 24

    All paths: [['A', 'C', 'D'], ['A', 'B', 'C', 'D'], ['A', 'B', 'D']]
        evaluating: ['A', 'C', 'D'] 16
        evaluating: ['A', 'B', 'C', 'D'] 20
        evaluating: ['A', 'B', 'D'] 15
Best path: A->B:5 B->D:10   Total: 15

    All paths: [['A', 'C', 'D', 'E', 'F'], ['A', 'B', 'C', 'D', 'E', 'F'], ['A', 'B', 'D', 'E', 'F']]
        evaluating: ['A', 'C', 'D', 'E', 'F'] 33
        evaluating: ['A', 'B', 'C', 'D', 'E', 'F'] 37
        evaluating: ['A', 'B', 'D', 'E', 'F'] 32
Best path: A->B:5 B->D:10 D->E:9 E->F:8   Total: 32