基于numpy/scipy的快速b样条算法
我需要用python计算bspline曲线。我看了看scipy.interpolate.splprep公司和其他一些scipy模块,但找不到任何能给我所需要的东西。所以我在下面写了我自己的模块。
代码运行得很好,但速度很慢(test函数运行时间为0.03s,看起来
就像很多考虑到我只要求100个样品和6个对照品
顶点)。有没有一种方法可以通过几个scipy模块调用来简化下面的代码想必会加速吗?如果没有,我该怎么处理我的代码提高它的性能?
import numpy as np
# cv = np.array of 3d control vertices
# n = number of samples (default: 100)
# d = curve degree (default: cubic)
# closed = is the curve closed (periodic) or open? (default: open)
def bspline(cv, n=100, d=3, closed=False):
# Create a range of u values
count = len(cv)
knots = None
u = None
if not closed:
u = np.arange(0,n,dtype='float')/(n-1) * (count-d)
knots = np.array([0]*d + range(count-d+1) + [count-d]*d,dtype='int')
else:
u = ((np.arange(0,n,dtype='float')/(n-1) * count) - (0.5 * (d-1))) % count # keep u=0 relative to 1st cv
knots = np.arange(0-d,count+d+d-1,dtype='int')
# Simple Cox - DeBoor recursion
def coxDeBoor(u, k, d):
# Test for end conditions
if (d == 0):
if (knots[k] <= u and u < knots[k+1]):
return 1
return 0
Den1 = knots[k+d] - knots[k]
Den2 = knots[k+d+1] - knots[k+1]
Eq1 = 0;
Eq2 = 0;
if Den1 > 0:
Eq1 = ((u-knots[k]) / Den1) * coxDeBoor(u,k,(d-1))
if Den2 > 0:
Eq2 = ((knots[k+d+1]-u) / Den2) * coxDeBoor(u,(k+1),(d-1))
return Eq1 + Eq2
# Sample the curve at each u value
samples = np.zeros((n,3))
for i in xrange(n):
if not closed:
if u[i] == count-d:
samples[i] = np.array(cv[-1])
else:
for k in xrange(count):
samples[i] += coxDeBoor(u[i],k,d) * cv[k]
else:
for k in xrange(count+d):
samples[i] += coxDeBoor(u[i],k,d) * cv[k%count]
return samples
if __name__ == "__main__":
import matplotlib.pyplot as plt
def test(closed):
cv = np.array([[ 50., 25., -0.],
[ 59., 12., -0.],
[ 50., 10., 0.],
[ 57., 2., 0.],
[ 40., 4., 0.],
[ 40., 14., -0.]])
p = bspline(cv,closed=closed)
x,y,z = p.T
cv = cv.T
plt.plot(cv[0],cv[1], 'o-', label='Control Points')
plt.plot(x,y,'k-',label='Curve')
plt.minorticks_on()
plt.legend()
plt.xlabel('x')
plt.ylabel('y')
plt.xlim(35, 70)
plt.ylim(0, 30)
plt.gca().set_aspect('equal', adjustable='box')
plt.show()
test(False)
The two images below shows what my code returns with both closed conditions:
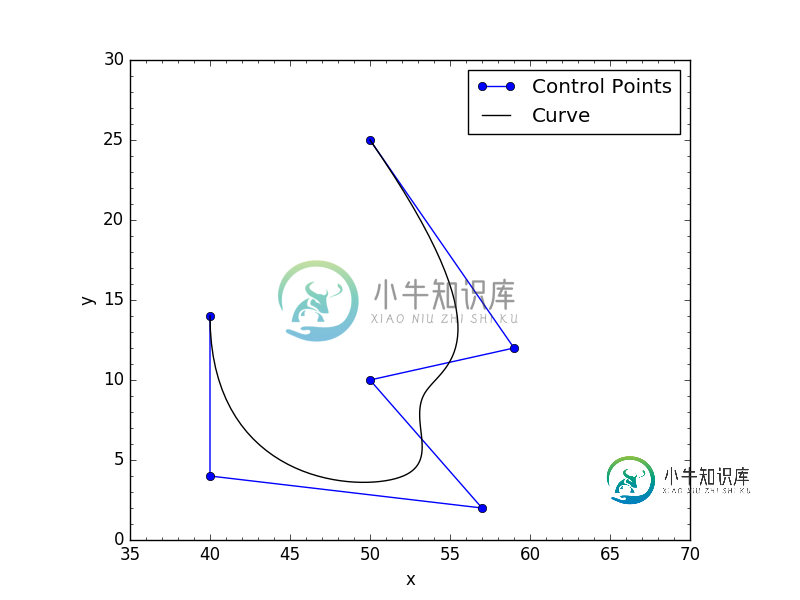
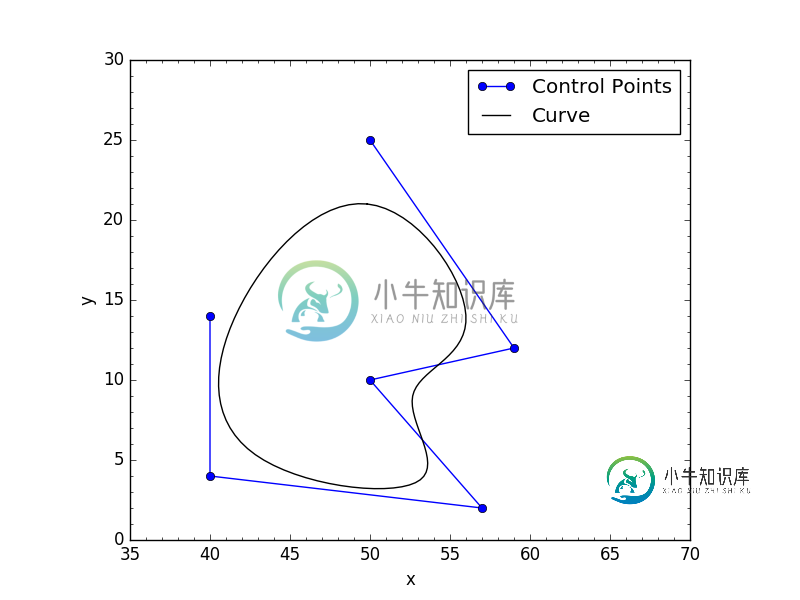
问题答案:
经过研究,我终于有了很多问题
我的回答。在scipy中一切都是可用的,我把我的代码放在这里
希望其他人能发现这个有用。
该函数采用N-d点数组、曲线阶数和周期状态
(打开或关闭)并将沿该曲线返回n个样本。有很多方法
以确保曲线样本是等距的,但目前我将
把注意力集中在这个问题上,因为它完全是关于速度的。
值得注意的是:我似乎无法超越20度的曲线。
当然,这已经是过分了,但我觉得值得一提。
同样值得注意的是:在我的机器上下面的代码可以计算100000
0.017s中的样品
import numpy as np
import scipy.interpolate as si
def bspline(cv, n=100, degree=3, periodic=False):
""" Calculate n samples on a bspline
cv : Array ov control vertices
n : Number of samples to return
degree: Curve degree
periodic: True - Curve is closed
False - Curve is open
"""
# If periodic, extend the point array by count+degree+1
cv = np.asarray(cv)
count = len(cv)
if periodic:
factor, fraction = divmod(count+degree+1, count)
cv = np.concatenate((cv,) * factor + (cv[:fraction],))
count = len(cv)
degree = np.clip(degree,1,degree)
# If opened, prevent degree from exceeding count-1
else:
degree = np.clip(degree,1,count-1)
# Calculate knot vector
kv = None
if periodic:
kv = np.arange(0-degree,count+degree+degree-1)
else:
kv = np.clip(np.arange(count+degree+1)-degree,0,count-degree)
# Calculate query range
u = np.linspace(periodic,(count-degree),n)
# Calculate result
return np.array(si.splev(u, (kv,cv.T,degree))).T
To test it:
import matplotlib.pyplot as plt
colors = ('b', 'g', 'r', 'c', 'm', 'y', 'k')
cv = np.array([[ 50., 25.],
[ 59., 12.],
[ 50., 10.],
[ 57., 2.],
[ 40., 4.],
[ 40., 14.]])
plt.plot(cv[:,0],cv[:,1], 'o-', label='Control Points')
for d in range(1,21):
p = bspline(cv,n=100,degree=d,periodic=True)
x,y = p.T
plt.plot(x,y,'k-',label='Degree %s'%d,color=colors[d%len(colors)])
plt.minorticks_on()
plt.legend()
plt.xlabel('x')
plt.ylabel('y')
plt.xlim(35, 70)
plt.ylim(0, 30)
plt.gca().set_aspect('equal', adjustable='box')
plt.show()
As of scipy-0.19.0 there is a new
scipy.interpolate.BSpline
function that can be used.
import numpy as np
import scipy.interpolate as si
def scipy_bspline(cv, n=100, degree=3, periodic=False):
""" Calculate n samples on a bspline
cv : Array ov control vertices
n : Number of samples to return
degree: Curve degree
periodic: True - Curve is closed
"""
cv = np.asarray(cv)
count = cv.shape[0]
# Closed curve
if periodic:
kv = np.arange(-degree,count+degree+1)
factor, fraction = divmod(count+degree+1, count)
cv = np.roll(np.concatenate((cv,) * factor + (cv[:fraction],)),-1,axis=0)
degree = np.clip(degree,1,degree)
# Opened curve
else:
degree = np.clip(degree,1,count-1)
kv = np.clip(np.arange(count+degree+1)-degree,0,count-degree)
# Return samples
max_param = count - (degree * (1-periodic))
spl = si.BSpline(kv, cv, degree)
return spl(np.linspace(0,max_param,n))
Testing for equivalency:
p1 = bspline(cv,n=10**6,degree=3,periodic=True) # 1 million samples: 0.0882 sec
p2 = scipy_bspline(cv,n=10**6,degree=3,periodic=True) # 1 million samples: 0.0789 sec
print np.allclose(p1,p2) # returns True
-
问题内容: 我希望学生解决作业中的二次程序,而不必安装诸如cvxopt等的额外软件。是否有仅依赖于NumPy / SciPy的python实现? 问题答案: 我遇到了一个很好的解决方案,想把它解决。NICTA之外的ELEFANT机器学习工具包中有一个LOQO的python实现(在本文中为http://elefant.forge.nicta.com.au)。看一看optimization.intpo
-
JavaScript算法-快速排序 快速排序是处理大数据集最快的排序算法之一。它是一种分而治之的算法,通过递归的方式将数据依次分解为包含较小元素和较大元素的不同子序列。该算法不断重复这个步骤直到所有数据都是有序的。 这个算法首先要在列表中选择一个元素作为基准值(pivot)。数据排序围绕基准值进行,将列表中小于基准值的元素移到数组的底部,将大于基准值的元素移到数组的顶部。 快速排序的算法和伪代码
-
本文向大家介绍基于javascript实现的快速排序,包括了基于javascript实现的快速排序的使用技巧和注意事项,需要的朋友参考一下 "妙味课堂"的一期视频教学。 主要原理是:快速排序的原理:找基准点、建立二个数组分别存储、递归 基准点:就是找到这个数组中间的一个数; 建立二个数组分别存储:就是以这个基准点,将它的左右数值,分别存放到两个定义的新数组当中; 递归:在函数内部调用自身;
-
本文向大家介绍Java基于分治法实现的快速排序算法示例,包括了Java基于分治法实现的快速排序算法示例的使用技巧和注意事项,需要的朋友参考一下 本文实例讲述了Java基于分治法实现的快速排序算法。分享给大家供大家参考,具体如下: 运行结果: PS:这里再为大家推荐一款关于排序的演示工具供大家参考: 在线动画演示插入/选择/冒泡/归并/希尔/快速排序算法过程工具: http://tools.jb51
-
问题内容: 我需要函数或函数。 有各种和功能,但我很惊讶地发现缺少的功能。 为了使事情正常,我一直在使用这种相当慢的替代方法 我的数组通常包含32,000个元素,因此这被证明是一个瓶颈。我很想尝试,和,但是我认为我应该在这里提出问题,因为可能会有更好的解决方案。 问题答案: 我有一个更快的机制,尽管您需要运行一些测试以查看准确性是否足够。 这是原始的exp / sum / log版本: 这是一个使
-
我怎样才能导入阶乘函数分别从Numpy和sippy为了看看哪一个更快? 我已经通过导入数学从python本身导入了阶乘。但是,它不适用于Numpy和smpy。

