android广角相机畸变校正算法和实现示例

1.光学相机镜头一般都存在畸变的问题,畸变属于成像的几何失真,它是由于焦平面上不同区域对影像的放大率不同而形成的画面扭曲变形现象。除了一些特定的场合，大部分情况下，这些失真都是需要校正到正常人眼不产生扭曲的程度。

2常见的畸变是枕形畸变，桶形畸变和线性畸变。广角镜头的摄像设备拍摄出来的图像经常会有桶形畸变的问题。原因在于广角镜头使用的是凸透镜，初中物理知识告诉我们凸透镜会对光线起汇聚作用，这是光的折射造成的。而离镜头中心越远，折射效果越强，因而其拍出来的照片会以镜头中心为圆心，呈圆形向外扩展失真。

3.摄像头精确校正需要先获取标定数据，可以利用张正友的张氏标定法，或者使用MATLAB标定。

4.一般摄像头畸变校正可以使用OPENCV，OpenCV的畸变参数总共有五个，径向畸变3个（k1,k2,k3）和切向畸变2个(p1,p2)。

径向畸变：

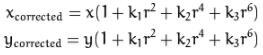
切向畸变：

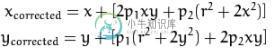
以及在OpenCV中的畸变系数的排列（这点一定要注意k1，k2，p1，p2，k3），千万不要以为k是连着的。

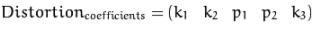
其公式由好像是泰勒公式，K和P应该可以无限精确，也可以横竖使用不同参数，r=x*X+y*y;

5.这里不对标定过程和opencv校正过程详细推理。这里使用代码实现简单的畸变算法，考虑到效率和实时性，略去切向畸变，径向畸变假设x,y相等且只取一阶K值，其实一阶K值大约已经可以把畸变控制人眼接受的范围内了。

6.代码

public class LensCorrect2 {
	// 镜头校正查找表
	private Point[][] CorrInd = null;// new Point[480][640];
	private double k1 = 0f;
	private double k2 = 0f;
	private Bitmap mBm = null;
	private int mW = 0;
	private int mH = 0;
 
	private int max_x = 0, max_y = 0;
	private int min_x = 0, min_y = 0;
 
	// 镜头径向畸变校正初始化
	public LensCorrect2(double k1, double k2, Bitmap mBm) {
		super();
		this.k1 = k1;
		this.k2 = k2;
		this.mBm = mBm;
 
		this.mW = mBm.getWidth();
		this.mH = mBm.getHeight();
 
		int cw = mW >> 1;
		int ch = mH >> 1;
		CorrInd = new Point[mH][mW];
		Log.i("XXXXX", "imgHeight=" + mH);
		Log.i("XXXXX", "imgWidth=" + mW);
 
		int it;
		int jt;
		int it2;
		int jt2;
 
		for (int i = 0; i < mH; i++) {
			it = (i + 1) - ch; // (i+1) 是其真正的图像坐标
			for (int j = 0; j < mW; j++) {
				double temp;
 
				jt = (j + 1) - cw; // (j+1) 是其真正的图像坐标
				temp = 1 + k1 * it * it + k2 * jt * jt;
				it2 = (int) (temp * it);
				jt2 = (int) (temp * jt);
 
				it2 = it2 + ch + 1;
				jt2 = jt2 + cw + 1;
 
				// Log.i("AAAAA", "imgHeight="+imgHeight);
				// Log.i("AAAAA", "imgWidth="+imgWidth);
				// Log.i("AAAAA", "i="+i);
				// Log.i("AAAAA", "j="+j);
 
				// Log.i("XXXXX", "jt2="+jt2);
				// Log.i("XXXXX", "it2="+it2);
				if (max_x < jt2) {
					max_x = jt2;
				}
				if (min_x > jt2) {
					min_x = jt2;
				}
				if (max_y < it2) {
					max_y = it2;
				}
				if (min_y > it2) {
					min_y = it2;
				}
 
				Point p = new Point(jt2, it2);
				CorrInd[i][j] = p;
 
			}
		}
		Log.i("XXXXX", "max_x=" + max_x);
		Log.i("XXXXX", "min_x=" + min_x);
		Log.i("XXXXX", "max_y=" + max_y);
		Log.i("XXXXX", "min_y=" + min_y);
	}
 
	public Bitmap getLensCorrect() {
		Bitmap bm = Bitmap.createBitmap((max_x - min_x) + 1,
				(max_y - min_y) + 1, Bitmap.Config.ARGB_8888);
 
		int it2;
		int jt2;
 
		for (int i = 0; i < mH; i++) {
			for (int j = 0; j < mW; j++) {
				it2 = CorrInd[i][j].y;
				jt2 = CorrInd[i][j].x;
 
				bm.setPixel(jt2 - min_x, it2 - min_y, mBm.getPixel(j, i));
 
			}
		}
		return bm;
	}
 
	public Bitmap getLensCorrect0() {
		Bitmap bm = Bitmap.createBitmap(mW, mH, Bitmap.Config.ARGB_8888);
 
		int it2;
		int jt2;
 
		for (int i = 0; i < mH; i++) {
			for (int j = 0; j < mW; j++) {
				it2 = CorrInd[i][j].y;
				jt2 = CorrInd[i][j].x;
 
				if ((it2 >= 0) && (jt2 >= 0) && (it2 < mH) && (jt2 < mW)) {
					// bm.setPixel(j, i, mBm.getPixel(jt2, it2));
					bm.setPixel(jt2, it2, mBm.getPixel(j, i));
				}
			}
		}
		return bm;
	}
 
}

7.下图对图像进行反畸变，由于用于测试的广角相机手机找不到了，没有找到合适的图片，使用一下没有变形的图片，对其做反桶形畸变，反畸变后，损失的像素需要插值补充完整

以上这篇android广角相机畸变校正算法和实现示例就是小编分享给大家的全部内容了，希望能给大家一个参考，也希望大家多多支持小牛知识库。