python实现拉普拉斯特征图降维示例

这种方法假设样本点在光滑的流形上，这一方法的计算数据的低维表达，局部近邻信息被最优的保存。以这种方式，可以得到一个能反映流形的几何结构的解。

步骤一：构建一个图G=(V,E),其中V={vi，i=1,2,3…n}是顶点的集合，E={eij}是连接顶点的vi和vj边，图的每一个节点vi与样本集X中的一个点xi相关。如果xi，xj相距较近，我们就连接vi，vj。也就是说在各自节点插入一个边eij，如果Xj在xi的k领域中，k是定义参数。

步骤二：每个边都与一个权值Wij相对应，没有连接点之间的权值为0，连接点之间的权值：

步骤三：令 ，实现广义本征分解：

使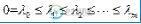 是最小的m+1个本征值。忽略与 =0相关的本征向量，选取另外m个本征向量即为降维后的向量。

1、python实现拉普拉斯降维

def laplaEigen(dataMat,k,t): 
 m,n=shape(dataMat) 
 W=mat(zeros([m,m])) 
 D=mat(zeros([m,m])) 
 for i in range(m): 
 k_index=knn(dataMat[i,:],dataMat,k) 
 for j in range(k): 
  sqDiffVector = dataMat[i,:]-dataMat[k_index[j],:] 
  sqDiffVector=array(sqDiffVector)**2 
  sqDistances = sqDiffVector.sum() 
  W[i,k_index[j]]=math.exp(-sqDistances/t) 
  D[i,i]+=W[i,k_index[j]] 
 L=D-W 
 Dinv=np.linalg.inv(D) 
 X=np.dot(D.I,L) 
 lamda,f=np.linalg.eig(X) 
return lamda,f 
def knn(inX, dataSet, k): 
 dataSetSize = dataSet.shape[0] 
 diffMat = tile(inX, (dataSetSize,1)) - dataSet 
 sqDiffMat = array(diffMat)**2 
 sqDistances = sqDiffMat.sum(axis=1) 
 distances = sqDistances**0.5 
 sortedDistIndicies = distances.argsort() 
return sortedDistIndicies[0:k] 
dataMat, color = make_swiss_roll(n_samples=2000) 
lamda,f=laplaEigen(dataMat,11,5.0) 
fm,fn =shape(f) 
print 'fm,fn:',fm,fn 
lamdaIndicies = argsort(lamda) 
first=0 
second=0 
print lamdaIndicies[0], lamdaIndicies[1] 
for i in range(fm): 
 if lamda[lamdaIndicies[i]].real>1e-5: 
 print lamda[lamdaIndicies[i]] 
 first=lamdaIndicies[i] 
 second=lamdaIndicies[i+1] 
 break 
print first, second 
redEigVects = f[:,lamdaIndicies] 
fig=plt.figure('origin') 
ax1 = fig.add_subplot(111, projection='3d') 
ax1.scatter(dataMat[:, 0], dataMat[:, 1], dataMat[:, 2], c=color,cmap=plt.cm.Spectral) 
fig=plt.figure('lowdata') 
ax2 = fig.add_subplot(111) 
ax2.scatter(f[:,first], f[:,second], c=color, cmap=plt.cm.Spectral) 
plt.show() 

2、拉普拉斯降维实验

用如下参数生成实验数据存在swissdata.dat里面：

def make_swiss_roll(n_samples=100, noise=0.0, random_state=None): 
 #Generate a swiss roll dataset. 
 t = 1.5 * np.pi * (1 + 2 * random.rand(1, n_samples)) 
 x = t * np.cos(t) 
 y = 83 * random.rand(1, n_samples) 
 z = t * np.sin(t) 
 X = np.concatenate((x, y, z)) 
 X += noise * random.randn(3, n_samples) 
 X = X.T 
 t = np.squeeze(t) 
return X, t 

实验结果如下：

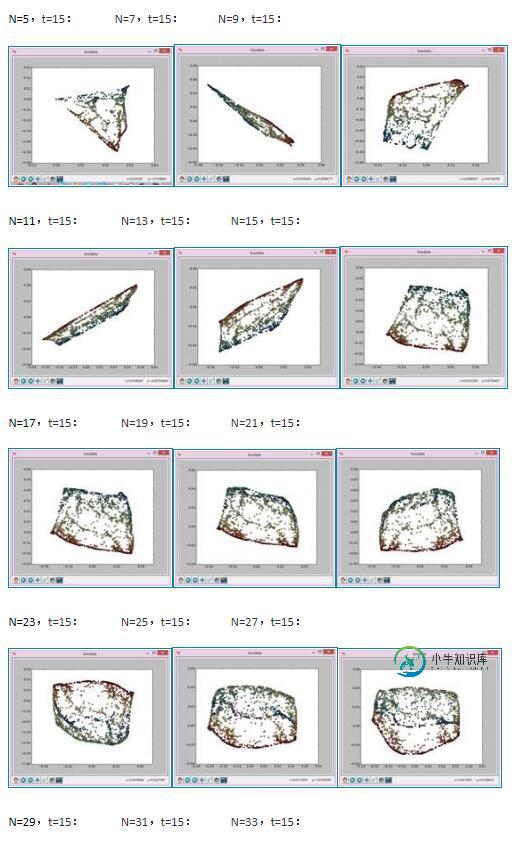
以上这篇python实现拉普拉斯特征图降维示例就是小编分享给大家的全部内容了，希望能给大家一个参考，也希望大家多多支持小牛知识库。