C++计数排序详解
计数排序不同于比较排序,是基于计数的方式,对于计数排序,假设每一个输入都是介于0~k之间的整数。对于每一个输入元素x,确定出小于x的元素的个数。假如有17个元素小于x,则x就属于第18个输出位置。
计数排序涉及到三个数组A[0…..length-1],length为数组A的长度;数组B与数组A长度相等,存放最终排序的结果;C[0…..K]存放A中每个元素的个数,k为数组A中的最大值。
int count_k(int A[],int length),此函数为了确定数组A中最大的元素,用来确定C数组的长度。
int count_k(int A[],int length)
{
int j,max;
max = A[0];
for(j=1;j<=length-1;j++)
{
if(A[j]>=max)
max = A[j];
}
return max;
}
计数排序的实现:
void count_sort(int A[],int B[],int k)
{
int *C = (int *)malloc((k+1) * sizeof(int));
int i,j;
for(i=0;i<=k;i++)//初始化数组C
C[i]=0;
for(j=0;j<=length-1;j++)//计算A中元素的个数
C[A[j]] = C[A[j]]+1;
for(i=1;i<=k;i++)//计算小于等于C[i]的元素的个数
C[i] = C[i] + C[i-1];
for(j=length-1;j>=0;j--)
{
int k=C[A[j]]-1;
B[k] = A[j];
C[A[j]] = C[A[j]] - 1;
}
free(C);
}
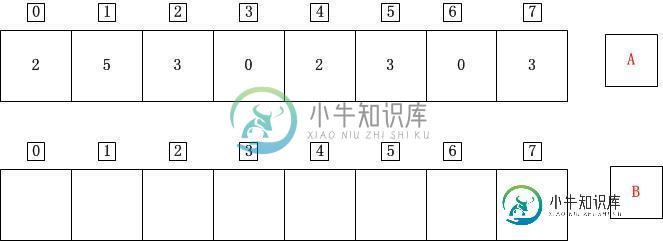
count_sort(A,B,k);
k=5
for(j=0;j<=length-1;j++)//计算A中元素的个数 C[A[j]] = C[A[j]]+1;
表示数组A中有2个0、0个1、2个2、3个3、0个4、1个5
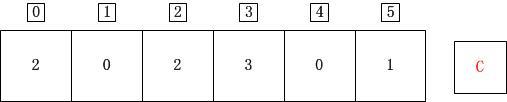
for(i=1;i<=k;i++)//计算小于等于C[i]的元素的个数 C[i] = C[i] + C[i-1];
小于等于0的数有两个,小于等于1的数有两个、小于等于2的数有4个、小于等于3的有7个、小于等于4的有7个、小于等于5的有8个

for(j=length-1;j>=0;j--)
{
int k=C[A[j]]-1;
B[k] = A[j];
C[A[j]] = C[A[j]] - 1;
}
for循环分析如下
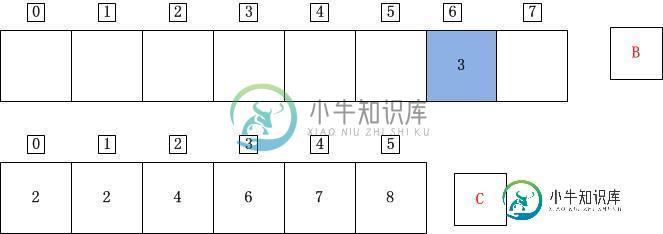
j=7;A[j]=A[7]=3;C[A[j]]=C[3]=7;C[A[j]]-1=6;B[C[A[j]]-1]=B[6]=A[j]=3;C[A[j]]=C[A[j]]-1=6
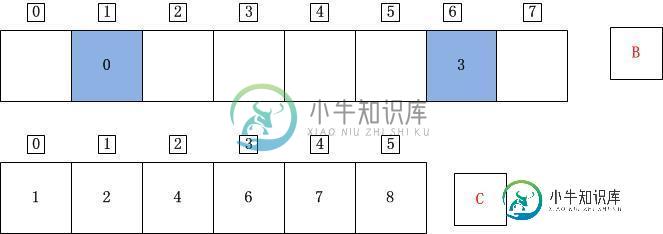
j=6;A[j]=A[6]=0;C[A[j]]=C[0]=2;C[A[j]]-1=1;B[C[A[j]]-1]=B[1]=A[j]=0;C[A[j]]=C[A[j]]-1=1
j=5;A[j]=A[5]=3;C[A[j]]=C[3]=6;C[A[j]]-1=5;B[C[A[j]]-1]=B[5]=A[j]=3;C[A[j]]=C[A[j]]-1=5;
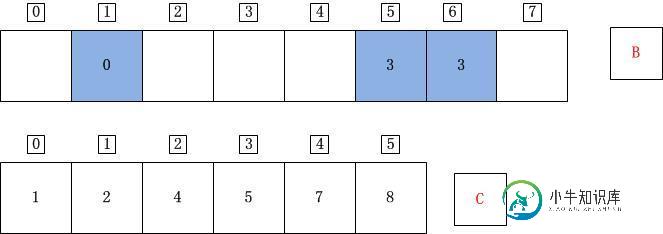
j=4;A[j]=A[4]=2;C[A[j]]=C[2]=4;C[A[j]]-1=3;B[C[A[j]]-1]=B[3]=A[j]=2;C[A[j]]=C[A[j]]-1=3;
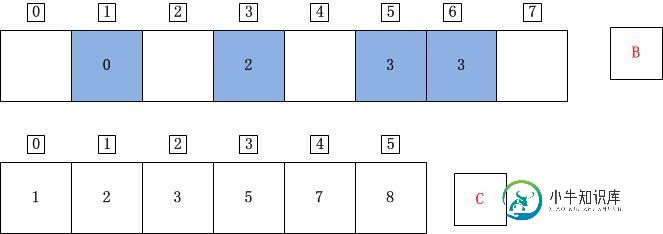
j=3;A[j]=A[3]=0;C[A[j]]=C[0]=1;C[A[j]]-1=0;B[C[A[j]]-1]=B[0]=A[j]=0;C[A[j]]=C[A[j]]-1=0;
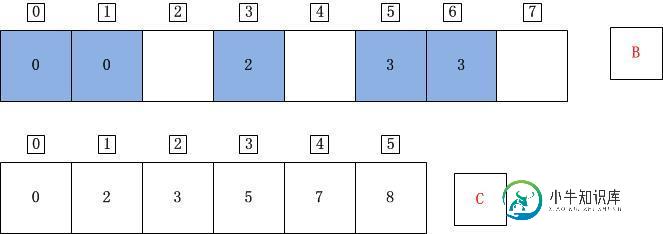
j=2;A[j]=A[2]=3;C[A[j]]=C[3]=5;C[A[j]]-1=4;B[C[A[j]]-1]=B[4]=A[j]=3;C[A[j]]=C[A[j]]-1=4;
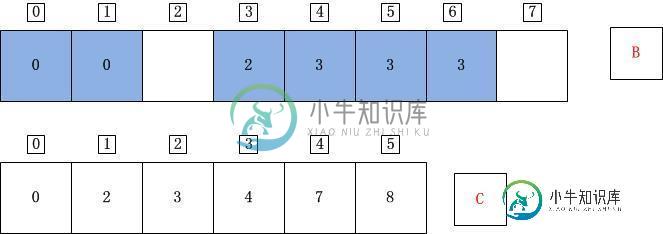
j=1;A[j]=A[1]=5;C[A[j]]=C[5]=8;C[A[j]]-1=7;B[C[A[j]]-1]=B[7]=A[j]=5;C[A[j]]=C[A[j]]-1=7;
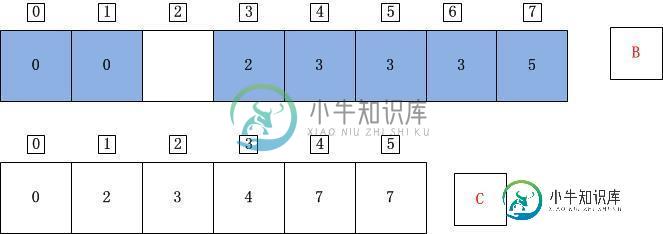
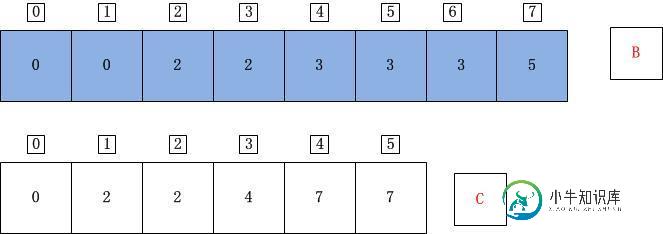
j=0;A[j]=A[0]=2;C[A[j]]=C[2]=3;C[A[j]]-1=2;B[C[A[j]]-1]=B[2]=A[j]=2;C[A[j]]=C[A[j]]-1=2;
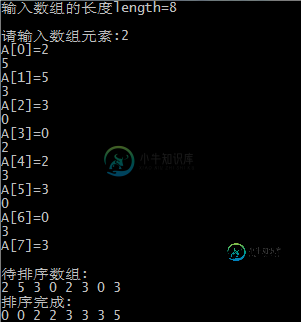
计数排序的最后运行截图
计数排序分析:j=length-1;j>=0;j–此处为倒序,是为了保证排序的稳定性,这个在基数排序中有重要的作用。
-
本文向大家介绍计数排序,包括了计数排序的使用技巧和注意事项,需要的朋友参考一下 计数排序是一种稳定的排序技术,用于根据较小的键对对象进行排序。它计算键值相同的键的数量。当不同键之间的差异不太大时,此排序技术非常有效,否则会增加空间复杂度。 计数排序技术的复杂性 时间复杂度:O(n + r) 空间复杂度:O(n + r) 输入输出 算法 输入:数据数组,数组中的总数 输出:排序后的数组 示例 输出结
-
计数排序的核心在于将输入的数据值转化为键存储在额外开辟的数组空间中。作为一种线性时间复杂度的排序,计数排序要求输入的数据必须是有确定范围的整数。 1. 动图演示 2. JavaScript 代码实现 function countingSort(arr, maxValue) { var bucket = new Array(maxValue+1), sortedIndex =
-
主要内容:计数排序算法的实现思路,计数排序算法的具体实现通过统计序列中各个元素出现的次数,完成对整个序列的升序或降序排序,这样的排序算法称为 计数排序算法。 接下来,我们为您系统地讲解计数排序算法。 计数排序算法的实现思路 假设待排序序列为 {4, 2, 2, 8, 3, 3, 1},使用计数排序算法完成升序排序的过程为: 1) 找到序列中的最大值(用 max 表示)。对于 {4, 2, 2, 8, 3, 3, 1} 序列来说,最大值是 8。 2) 创
-
因此,我理解了使用合并排序对数组中的反转进行计数的一般思路。在合并过程中,您可以递归地计算左子数组和右子数组中的倒数。 这是我为此编写的一些代码。 我很难理解的是为什么在向其附加元素之前必须清除函数中的数组?有没有其他方法可以不清除数组?我问是因为我习惯于用编写合并排序
-
本文向大家介绍JS排序之快速排序详解,包括了JS排序之快速排序详解的使用技巧和注意事项,需要的朋友参考一下 本文为大家分享了JS快速排序的具体代码,供大家参考,具体内容如下 说明 时间复杂度指的是一个算法执行所耗费的时间 空间复杂度指运行完一个程序所需内存的大小 稳定指,如果a=b,a在b的前面,排序后a仍然在b的前面 不稳定指,如果a=b,a在b的前面,排序后可能会交换位置 --JS快速排序--
-
本文向大家介绍JS排序之选择排序详解,包括了JS排序之选择排序详解的使用技巧和注意事项,需要的朋友参考一下 本文为大家分享了JS选择排序的具体代码,供大家参考,具体内容如下 说明 时间复杂度指的是一个算法执行所耗费的时间 空间复杂度指运行完一个程序所需内存的大小 稳定指,如果a=b,a在b的前面,排序后a仍然在b的前面 不稳定指,如果a=b,a在b的前面,排序后可能会交换位置 --JS选择排序--

