Java算法之堆排序代码示例

堆是一种特殊的完全二叉树，其特点是所有父节点都比子节点要小，或者所有父节点都比字节点要大。前一种称为最小堆，后一种称为最大堆。

比如下面这两个：

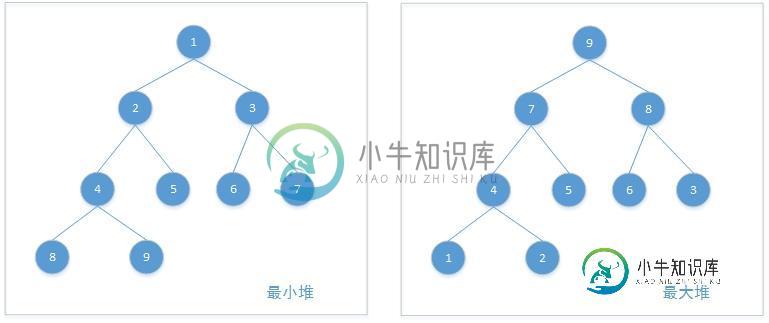
 那么这个特性有什么作用？既然题目是堆排序，那么肯定能用来排序。想要用堆排序首先要创建一个堆，如果对4 3 6 2 7 1 5这七个数字做从小到大排序，需要用这七个数创建一个最大堆，来看代码：

public class HeapSort {
  private int[] numbers;
  private int length;
  public HeapSort(int[] numbers) {
    this.numbers = numbers;
    this.length = numbers.length;
  }
  /**
   * 调整二叉树
   * 如果父节点编号为x, 那么左子节点的编号是2x, 右子节点的编号是2x+1
   * 节点编号从1开始, 对应数组中的索引是编号-1
   * @param nodeId 节点编号, 从1开始
   */
  public void adjust(int nodeId) {
    int swapId;
    int flag = 0; //是否需要继续向下调整
    while(nodeId * 2 <= this.length && flag == 0) {
      //首先判断它和左子节点的关系, 并用swapId记录值较小的节点编号(最大堆是记录较大的)
      int index = nodeId - 1; //节点对应数组中数字的索引
      int leftChild = nodeId * 2 - 1; //左子节点对应数组中数字的索引
      int rightChild = nodeId * 2; //右子节点对应数组中数字的索引
      if(numbers[index] < numbers[leftChild]) {
        swapId = nodeId * 2;
      } else {
        swapId = nodeId;
      }
      //如果有右子节点, 再与右子节点比较
      if(nodeId * 2 + 1 <= this.length) {
        if(numbers[swapId - 1] < numbers[rightChild])
          swapId = nodeId * 2 + 1;
      }
      //如果最小的节点编号不是自己, 说明子节点中有比父节点更小的
      if(swapId != nodeId) {
        swap(swapId, nodeId);
        nodeId = swapId;
      } else {
        flag = 1;
      }
    }
  }
  /**
   * 交换两个节点的值
   * @param nodeId1
   * @param nodeId2
   */
  public void swap(int nodeId1, int nodeId2) {
    int t = numbers[nodeId1 - 1];
    numbers[nodeId1 - 1] = numbers[nodeId2 - 1];
    numbers[nodeId2 - 1] = t;
  }
  /**
   * 创建最大堆
   */
  public void createMaxHeap() {
    //从最后一个非叶节点到第一个节点依次向上调整
    for(int i = this.length / 2; i >= 1; i--) {
      adjust(i);
    }
  }
  public static void main(String[] args) {
    int[] numbers = new int[] { 4, 3, 6, 2, 7, 1, 5 };
    for(int x = 0; x < numbers.length; x++) {
      System.out.print(numbers[x] + " ");
    }
    System.out.println();
    HeapSort heap = new HeapSort(numbers);
    heap.createMaxHeap();
  }
}

对本例中的数列，从this.length / 2到1，共执行了三轮循环。

第一轮：

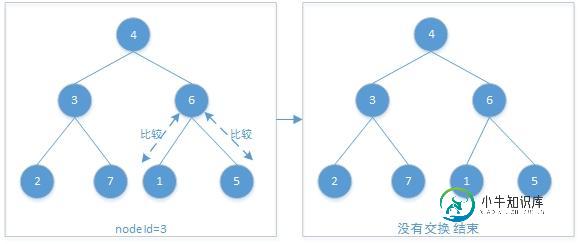
第二轮：

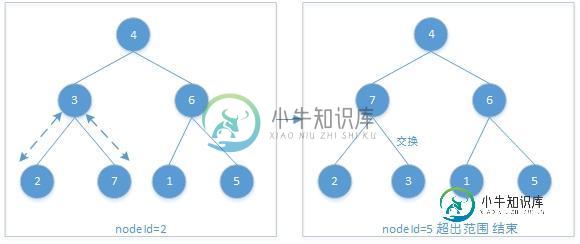
第三轮：

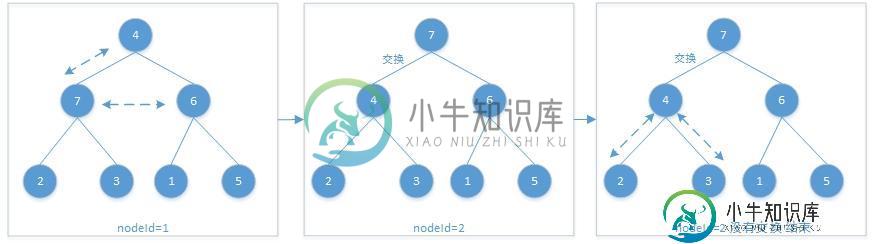
调整完成后，当前的二叉树已经符合最大堆的特性，可以用来从小到大排序。堆排序的原理是，交换堆顶和最后一个节点的数字，即把最大的数字放到数组最后，然后对除了最大数的前n-1个数从新执行调整过程，使其符合最大堆特性。重复以上过程直到堆中只剩下一个数字。

public void sort() {
  while(this.length > 1) {
    swap(1, this.length);
    this.length--;
    adjust(1);
  }
  for(int x = 0; x < numbers.length; x++) {
    System.out.print(numbers[x] + " ");
  }
}

堆排序的时间复杂度和快速排序的平均时间复杂度一样，是O(nlogn)。

总结

以上就是本文关于Java算法之堆排序代码示例的全部内容，希望对大家有所帮助。感兴趣的朋友可以继续参阅本站：java实现的各种排序算法代码示例、Java遗传算法之冲出迷宫等，有什么问题可以随时留言，小编会及时回复大家的。感谢朋友们对本站的支持！