JAVA堆排序算法的讲解
预备知识
堆排序
堆排序是利用堆这种数据结构而设计的一种排序算法,堆排序是一种选择排序,它的最坏,最好,平均时间复杂度均为O(nlogn),它也是不稳定排序。首先简单了解下堆结构。
堆
堆是具有以下性质的完全二叉树:每个结点的值都大于或等于其左右孩子结点的值,称为大顶堆;或者每个结点的值都小于或等于其左右孩子结点的值,称为小顶堆。如下图:
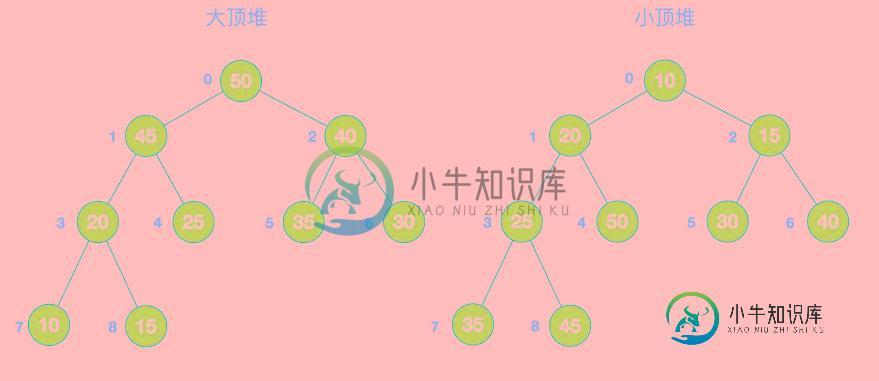
同时,我们对堆中的结点按层进行编号,将这种逻辑结构映射到数组中就是下面这个样子

该数组从逻辑上讲就是一个堆结构,我们用简单的公式来描述一下堆的定义就是:
大顶堆:arr[i] >= arr[2i+1] && arr[i] >= arr[2i+2]
小顶堆:arr[i] <= arr[2i+1] && arr[i] <= arr[2i+2]
ok,了解了这些定义。接下来,我们来看看堆排序的基本思想及基本步骤:
堆排序基本思想及步骤
堆排序的基本思想是:将待排序序列构造成一个大顶堆,此时,整个序列的最大值就是堆顶的根节点。将其与末尾元素进行交换,此时末尾就为最大值。然后将剩余n-1个元素重新构造成一个堆,这样会得到n个元素的次小值。如此反复执行,便能得到一个有序序列了
步骤一 构造初始堆。将给定无序序列构造成一个大顶堆(一般升序采用大顶堆,降序采用小顶堆)。
1.假设给定无序序列结构如下

2.此时我们从最后一个非叶子结点开始(叶结点自然不用调整,第一个非叶子结点 arr.length/2-1=5/2-1=1,也就是下面的6结点),从左至右,从下至上进行调整。

3.找到第二个非叶节点4,由于[4,9,8]中9元素最大,4和9交换。
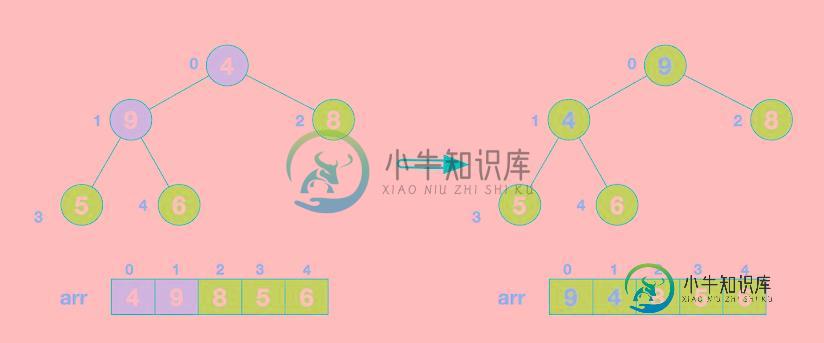
这时,交换导致了子根[4,5,6]结构混乱,继续调整,[4,5,6]中6最大,交换4和6。
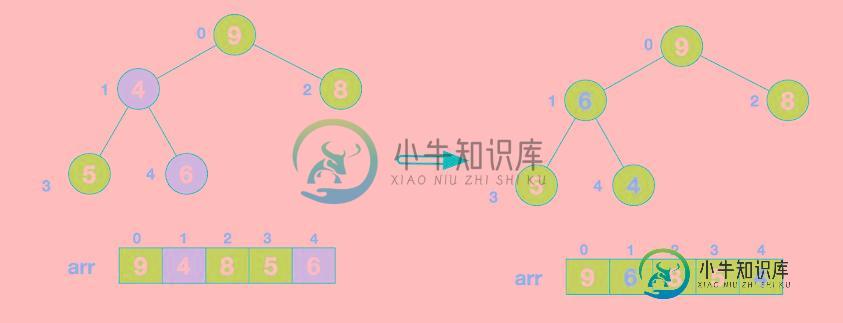
此时,我们就将一个无需序列构造成了一个大顶堆。
步骤二 将堆顶元素与末尾元素进行交换,使末尾元素最大。然后继续调整堆,再将堆顶元素与末尾元素交换,得到第二大元素。如此反复进行交换、重建、交换。
a.将堆顶元素9和末尾元素4进行交换

b.重新调整结构,使其继续满足堆定义
3607650429c.jpg" />
后续过程,继续进行调整,交换,如此反复进行,最终使得整个序列有序
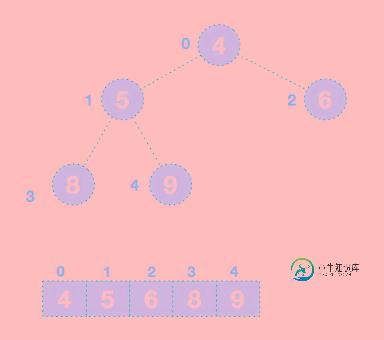
再简单总结下堆排序的基本思路:
a.将无需序列构建成一个堆,根据升序降序需求选择大顶堆或小顶堆;
b.将堆顶元素与末尾元素交换,将最大元素"沉"到数组末端;
c.重新调整结构,使其满足堆定义,然后继续交换堆顶元素与当前末尾元素,反复执行调整+交换步骤,直到整个序列有序。
代码实现
package sortdemo;
import java.util.Arrays;
/**
* Created by chengxiao on 2016/12/17.
* 堆排序demo
*/
public class HeapSort {
public static void main(String []args){
int []arr = {9,8,7,6,5,4,3,2,1};
sort(arr);
System.out.println(Arrays.toString(arr));
}
public static void sort(int []arr){
//1.构建大顶堆
for(int i=arr.length/2-1;i>=0;i--){
//从第一个非叶子结点从下至上,从右至左调整结构
adjustHeap(arr,i,arr.length);
}
//2.调整堆结构+交换堆顶元素与末尾元素
for(int j=arr.length-1;j>0;j--){
swap(arr,0,j);//将堆顶元素与末尾元素进行交换
adjustHeap(arr,0,j);//重新对堆进行调整
}
}
/**
* 调整大顶堆(仅是调整过程,建立在大顶堆已构建的基础上)
* @param arr
* @param i
* @param length
*/
public static void adjustHeap(int []arr,int i,int length){
int temp = arr[i];//先取出当前元素i
for(int k=i*2+1;k<length;k=k*2+1){//从i结点的左子结点开始,也就是2i+1处开始
if(k+1<length && arr[k]<arr[k+1]){//如果左子结点小于右子结点,k指向右子结点
k++;
}
if(arr[k] >temp){//如果子节点大于父节点,将子节点值赋给父节点(不用进行交换)
arr[i] = arr[k];
i = k;
}else{
break;
}
}
arr[i] = temp;//将temp值放到最终的位置
}
/**
* 交换元素
* @param arr
* @param a
* @param b
*/
public static void swap(int []arr,int a ,int b){
int temp=arr[a];
arr[a] = arr[b];
arr[b] = temp;
}
}
结果
[1, 2, 3, 4, 5, 6, 7, 8, 9]
最后
堆排序是一种选择排序,整体主要由构建初始堆+交换堆顶元素和末尾元素并重建堆两部分组成。其中构建初始堆经推导复杂度为O(n),在交换并重建堆的过程中,需交换n-1次,而重建堆的过程中,根据完全二叉树的性质,[log2(n-1),log2(n-2)...1]逐步递减,近似为nlogn。所以堆排序时间复杂度一般认为就是O(nlogn)级。
以上就是JAVA堆排序算法的讲解的详细内容,更多关于JAVA 堆排序算法的资料请关注小牛知识库其它相关文章!
-
给定一个堆栈,任务是对它进行排序,使堆栈的顶部具有最大的元素。 示例1: 输入:堆栈:3 2 1输出:3 2 1示例2: 输入:堆栈:11 2 32 3 41输出:41 32 11 3 2 您的任务: 预期时间复杂度:O(N*N)预期辅助空间:O(N)递归。 约束:1
-
示例数据 # heapq_heapdata.py # This data was generated with the random module. data = [19, 9, 4, 10, 11] # heapq_showtree.py import math from io import StringIO def show_tree(tree, total_width=36, fil
-
本文向大家介绍C#排序算法之堆排序,包括了C#排序算法之堆排序的使用技巧和注意事项,需要的朋友参考一下 本文实例为大家分享了C#实现堆排序的具体代码,供大家参考,具体内容如下 代码: 以上就是本文的全部内容,希望对大家的学习有所帮助,也希望大家多多支持呐喊教程。
-
本文向大家介绍Javascript堆排序算法详解,包括了Javascript堆排序算法详解的使用技巧和注意事项,需要的朋友参考一下 堆排序分为两个过程: 1.建堆。 堆实质上是完全二叉树,必须满足:树中任一非叶子结点的关键字均不大于(或不小于)其左右孩子(若存在)结点的关键字。 堆分为:大根堆和小根堆,升序排序采用大根堆,降序排序采用小根堆。 如果是大根堆,则通过调整函数将值最大的节点调整至堆根。
-
哪种排序算法适合对堆栈进行排序以提高空间效率?我需要对堆栈进行“就地”排序。此外,我对“就地”算法的理解是它们不使用任何其他数据结构 - 这是正确的吗? 我知道这与这个问题相似,但我想知道堆栈是否会有所不同?我知道堆栈可以只是一种链接列表,但是你只能访问顶部的事实会改变你的做法吗?
-
本文向大家介绍PHP实现排序堆排序(Heap Sort)算法,包括了PHP实现排序堆排序(Heap Sort)算法的使用技巧和注意事项,需要的朋友参考一下 算法引进: 在这里我直接引用《大话数据结构》里面的开头: 在前面讲到 简单选择排序 ,它在待排序的 n 个记录中选择一个最小的记录需要比较 n - 1 次,本来这也可以理解,查找第一个数据需要比较这么多次是正常的,否则如何知道他是最小的记录。

