OpenGL ES 矩阵变换及其数学原理详解(五)
引子
- 向量刻画的是线性空间中的对象。
- 矩阵刻画的是向量在线性空间中的运动(变换,跃迁),相似矩阵本质上就是同一个线性变换的不同的描述。
- 在一个线性空间中,选定了一组基,对于任何一个线性变化都可以用一个确定的矩阵来描述
- 矩阵不仅可以作为线性变换的描述,而且可以作为一组基的描述,作为变换的矩阵,不但可以把线性空间中的一个点给变换到另一个点去,而且也能够把线性空间中的一个坐标系(基)表换到另一个坐标系(基)去。
- 当我们谈到向量时,一定要指定它所在的坐标系才有意义,比如向量b=(1,2,3)实际上指的是在单位坐标系I下有一个向量的度量为b。
- 就可以理解Ma=b就可以看成Ma=Ib,就是说在坐标系M中度量出来的向量a和在坐标系I里面度量出来的b实际上就是同一个向量。
- 对于矩阵而言,他表示出来的那个坐标系也是由一组基(向量)组成的,同样存在这组基实在哪个坐标系下度量的问题。对于矩阵M,将其理解成IM,即M中的那组向量是在I坐标系中得出的。
- MxN本质是声明了一个在M坐标系中量出的另一个坐标系N,其中M本身是在I坐标系中度量出来的。
- 对坐标系施加变换的方法,就是让表示那个坐标系的矩阵与表示那个变化的矩阵相乘。
因此我们来理解这样一个式子,ACb,AC为矩阵,b为一个向量
- b是一个向量,他是在I坐标系下度量的,a = Cb也就是在I坐标系下将向量b变换到向量b,d=ACb=Aa的含义就是继续在I坐标系下将向量a变换到向量d。即在同一个坐标系I下面进行了两次变换操作。
- 另一种理解方式是ACb=IACb,那么IAC三个矩阵相乘就表示了坐标系的变换,在I坐标系中度量处新的坐标系IA,再在IA坐标系下度量出IAC,然后这里最终的坐标系中的向量b和在1中在I坐标系中经过两次变换得到的向量是同一个向量。
上面的两种理解方式也揭示了对向量的变换和对坐标系的变换是等价的,这一点也可以通过后面旋转变换的图示中看出来。
各种变换
平移矩阵

缩放矩阵

平移矩阵和缩放矩阵很容易理解,并且从矩阵形式我们也可以看到为什么用四维的向量表示一个顶点了,除了w分量用来做透视除法以外,另一个作用不也正好是为了把平移整合进来吗,都做乘法而不做加法。在数学上也就是将三维空间的坐标表示成其齐次形式.
旋转变换
旋转变换相对来说较为复杂,对绕x、y或z轴旋转的情况比较好理解。
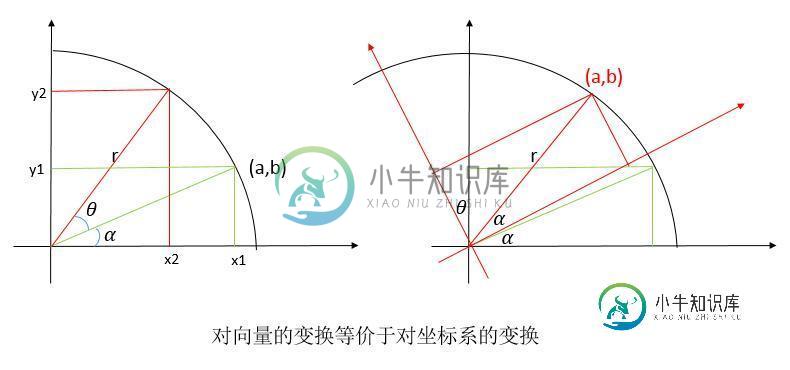
以绕z轴旋转为例

于是
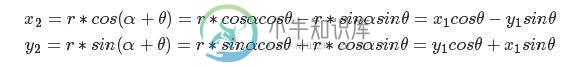
写成矩阵形式为

绕任意轴旋转的旋转矩阵为
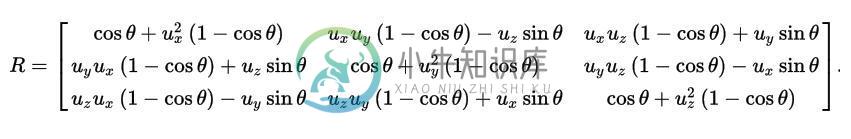
同理,前面学到的正交投影矩阵,透视矩阵以及摄像机矩阵,本质上和上面的变换都是一样的。
前面可以看到一般传入渲染管线的是一个由摄像机矩阵,投影矩阵,变换矩阵相乘得到的总的变换矩阵,
在顶点着色器中一般是这样的形式
gl_Position = uMVPMatrix * vec4(aPosition,1);
上面的代码中的变量uMVPMatrix表示了模型(M)、视图(V)、投影(P)三中变换综合,

注意到矩阵乘法的顺序,对每个点所做的变换是有顺序的,对每个点先进行模型变换(平移缩放旋转)、再进行视图变换(摄像机视角)再进行投影变换,这三个变换顺序是不可变得,因为改变顺序最终看到的效果都是不一样的。
对每个点所做的综合变换本质上就是对这个点进行矩阵相乘,然而就我们传入的是最终的综合变换矩阵而言,刚才的理解不是特别准确,换个思路理解成综合变换矩阵就是对坐标系的变换会更好,因为毕竟我们是一次性将这个相乘后的综合矩阵传进去的。
以上就是本文的全部内容,希望对大家的学习有所帮助,也希望大家多多支持小牛知识库。
-
变换矩阵 之前三节所说的坐标变换的三种方式——平移translate(),缩放scale(),以及旋转rotate()都可以通过transform()做到。 在介绍矩阵变换transform()前,我们来说一说什么是变换矩阵。 以上是Canvas中transform()方法所对应的变换矩阵。而此方法正是传入图中所示的六个参数,具体为context.transform(a,b,c,d,e,f)。 各
-
Three.js使用matrix编码3D变换 —— 平移(位置),旋转和缩放。 Object3D的每个实例都有一个matrix,用于存储该对象的位置,旋转和比例。本页介绍如何更新对象的变换。 便利的属性和matrixAutoUpdate(Convenience properties and matrixAutoUpdate) 有两种方法可以更新对象的转换: 修改对象的position,quater
-
成员变量 变量 类型 名称 备注 matrix Object 矩阵 scale Object 缩放 position Object 位置 rotation Object 旋转 localPivot Object 中枢 localAnchor Object 锚点 矩阵 例子: var tex = new BK.Texture("GameRes://resource/texture/star.png"
-
问题内容: 我正在使用阴影中的形状生成使用安装在移动平台上的相机拍摄的图像的数字地形模型(DTM)。用Python编写的算法似乎运行得很好,但是输出是倾斜的并且有点球形,所以我怀疑我需要从DTM中消除透视失真和桶形。 如果有人对此感兴趣,可以在这里获得数据。 摄像机以41度倾斜安装,并具有以下摄像机和失真矩阵: 如何应用透视变换并从此矩阵中消除桶形失真以获得平坦的DTM? 我已经尝试过使用Open
-
本文向大家介绍spring事务Propagation及其实现原理详解,包括了spring事务Propagation及其实现原理详解的使用技巧和注意事项,需要的朋友参考一下 本文研究的主要是spring事务Propagation及其实现原理,具体介绍如下。 简介 spring目前已是java开发的一个事实标准,这得益于它的便利、功能齐全、容易上手等特性。在开发过程当中,操作DB是非常常见的操作,而涉
-
本文向大家介绍PHP常量及变量区别原理详解,包括了PHP常量及变量区别原理详解的使用技巧和注意事项,需要的朋友参考一下 常量: 用于储存一个不会变化也不希望变化的数据的标示符(命名规则与变量相同) 定义形式: 使用 define() 函数定义 使用形式:define(“常量名” ,常量值) 使用 counst 语法定义 使用形式:counst 常量名 = 常量值 使用常量:有两种形式1,直接使用名

