C++实现第K顺序统计量的求解方法

一个n个元素组成的集合中，第K个顺序统计量（Order Statistic）指的是该集合中第K小的元素，我们这里要讨论的是如何在线性时间（linear time）里找出一个数组的第K个顺序统计量。该问题的算法对于C++程序员来说有一定的借鉴价值。具体如下：

一、问题描述：

问题：给定一个含有n个元素的无序数组，找出第k小的元素。

k = 1 ：最小值
k = n ：最大值
k = ⌊(n+1)/2⌋ or ⌈(n+1)/2⌉ ：中位数

找最大值或最小值很简单，只需要遍历一次数组并记录下最大值或最小值就可以了。我们在这里要解决的问题是一般性的选择问题。

一种原始的解决方案是，用堆排序或归并排序将输入数据进行排序，然后返回第k个元素。这样在Θ(nlgn)时间内一定可以解决。但是我们希望有更好的方案，最好是线性时间。

二、期望线性时间的解决方案：

为了在线性时间内解决这个选择问题，我们使用一个随机的分治算法，即RANDOMIZED-SELECT算法。此算法是使用随机化的快速排序中的随机划分子程序，对输入数组进行随机划分操作，然后判断第k小元素在划分后的哪个区域，对所在区域进行递归划分，最后找到第k小元素。

伪代码如下：

RANDOMIZED-SELECT(A,p,q,i) // i-th smallest in A[p..q] 
  if p = q 
    then return A[p] 
  r = RANDOMIZED-PARTITION(A, p, q) 
  k = r-p+1  // A[r] is k-th smallest 
  if i=k 
    then return A[r] 
  if i<k 
    then return RANDOMIZED-SELECT(A, p, r-1, i) 
  else 
    then return RANDOMIZED-SELECT(A, r+1, q, i-k) 

这里的RANDOMIZED-PARTITION()是随机版的划分操作（快速排序的分析与优化），可见本算法是一个随机算法，它的期望时间是Θ(n)（假设元素的值是不同的）。

1、Lucky-Case：最好的情况是在正中划分，划分的右边和右边的元素数量相等，但是1/10和9/10的划分也几乎一样好。可以这么说，任何常数比例的划分都和1/2:1/2的划分一样好。这里以1/10和9/10的划分为例，算法运行时间递归式为T(n) <= T(9n/10) + Θ(n)，根据主定理得到T(n) <= Θ(n)。

2、Unlucky-Case：虽然主元的选取是随机的，但是如果你运气足够差，每次都得到0：n-1的划分，这就是最坏的情况。此时递归式为T(n) = T(n-1) + Θ(n)，则时间复杂度为T(n) = Θ(n^2)。

3、Expected-Time：期望运行时间为Θ(n)，即线性时间。这里就不证明了，证明需要用到指示器随机变量。

C++代码如下：

/************************************************************************* 
  > File Name: RandomizedSelect.cpp 
  > Author: SongLee 
 ************************************************************************/ 
#include<iostream> 
#include<cstdlib> // srand rand 
using namespace std; 
 
void swap(int &a, int &b) 
{ 
  int tmp = a; 
  a = b; 
  b = tmp; 
} 
 
int Partition(int A[], int low, int high) 
{ 
  int pivot = A[low]; 
  int i = low; 
  for(int j=low+1; j<=high; ++j) 
  { 
    if(A[j] <= pivot) 
    { 
      ++i; 
      swap(A[i], A[j]); 
    } 
  } 
  swap(A[i], A[low]); 
  return i; 
} 
 
int Randomized_Partition(int A[], int low, int high) 
{ 
  srand(time(NULL)); 
  int i = rand() % (high+1); 
  swap(A[low], A[i]); 
  return Partition(A, low, high); 
} 
 
int Randomized_Select(int A[], int p, int q, int i) 
{ 
  if(p == q) 
    return A[p]; 
  int r = Randomized_Partition(A, p, q); 
  int k = r-p+1; 
  if(i == k) 
    return A[r]; 
  if(i < k) 
    return Randomized_Select(A, p, r-1, i); 
  else 
    return Randomized_Select(A, r+1, q, i-k); 
} 
 
/* 测试 */ 
int main() 
{ 
  int A[] = {6,10,13,5,8,3,2,11}; 
  int i = 7; 
  int result = Randomized_Select(A, 0, 7, i); 
  cout << "The " << i << "th smallest element is " << result << endl; 
  return 0; 
} 

三、最坏情况线性时间的解决方案

虽然最坏情况Θ(n2)出现的概率非常非常小，但是不代表它不会出现。这里就介绍一个非同一般的算法，以保证在最坏情况下也能达到线性时间。

这个SELECT算法的基本思想就是要保证对数组的划分是一个好的划分，它通过自己的方法选取主元（pivot），然后将pivot作为参数传递给快速排序的确定性划分操作PARTITION。

基本步骤：

①.将输入数组的n个元素划分为n/5（上取整）组，每组5个元素，且至多只有一个组有剩下的n%5个元素组成。

②.寻找每个组织中中位数。首先对每组中的元素（至多为5个）进行插入排序，然后从排序后的序列中选择出中位数。

③.对第2步中找出的n/5（上取整）个中位数，递归调用SELECT以找出其中位数x。（如果是偶数取下中位数）

④.调用PARTITION过程，按照中位数x对输入数组进行划分。确定中位数x的位置k。

⑤.如果i=k，则返回x。否则，如果i < k，则在地区间递归调用SELECT以找出第i小的元素，若干i > k，则在高区找第(i-k)个最小元素。

如下图所示：

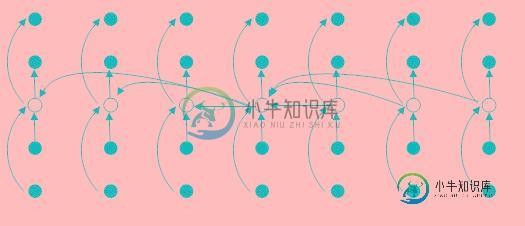
总结：

RANDOMIZED-SELECT和SELECT算法是基于比较的。我们知道，在比较模型中，排序时间不会优于Ω(nlgn)。之所以这里的选择算法达到了线性时间，是因为它们没有使用排序就解决了选择问题。另外，我们没有使用线性时间排序算法（计数排序/桶排序/基数排序），是因为它们要达到线性时间对输入有很高的要求，而这里不需要关于输入的任何假设。