Java实现布隆过滤器的方法步骤

前言

记得前段时间的文章么？redis使用位图法记录在线用户的状态，还是需要自己实现一个IM在线用户状态的记录，今天来讲讲另一方案，布隆过滤器

布隆过滤器的作用是加快判定一个元素是否在集合中出现的方法。因为其主要是过滤掉了大部分元素间的精确匹配，故称为过滤器。

布隆过滤器

在日常生活工作，我们会经常遇到这的场景，从一个Excel里面检索一个信息在不在Excel表中，还记得被CTRL+F支配的恐惧么，不扯了，软件开发中，一般会使用散列表来实现，Hash Table也叫哈希表，哈希表的优点是快速准确，缺点是浪费储存空间，我们这个场景，储存登录的userId到哈希表，当用户规模十分巨大的时候，哈希表的储存效率低的问题就显示出来了，今天介绍一种数学工具：布隆过滤器，它只需要哈希表1/8到1/4的大小就能解决同样的问题。

背书中

布隆过滤器（Bloom Filter）是由伯顿·布隆（Burton Bloom）于1970年提出来的，它实际上是一个很长的二进制向量和一系列随机映射函数。

原理

使用我们这个场景，来讲原理吧，假设我们的个人网站同时在线人数达到1亿（意淫一下），要存储这一亿人的在线状态，先构建一个16亿比特位即两亿字节的向量，然后把这16亿个比特位都记为0。对于每一个登录用的userId，使用8个不同的算法产出8个不同信息指纹，在用一个算法把这8个信息隐身到这16亿个比特位的8个位置上，把这8个位置都设置成1，这样就构建成了一个记录一亿用户在线状态的布隆过滤器。

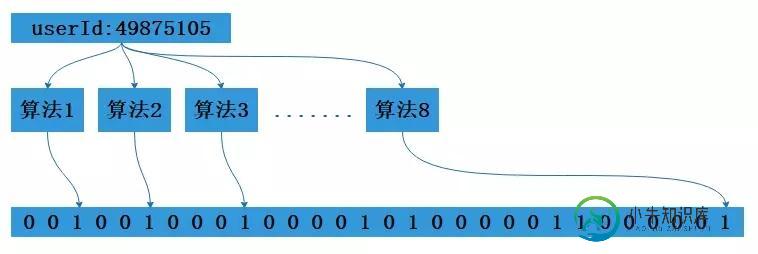
1亿在线用户的布隆过滤器

检索就是同样的原理，使用相同的算法对要检索的userId产生8个信息指纹，然后在看这八个信息指纹在这16亿比特位对应的值是否为1，都为1就说明这个userId在线，下面就用java代码来实现一个布隆过滤器。

Java实现布隆过滤器

先实现一个简单的布隆过滤器

package edu.se;

import java.util.BitSet;

/**
 * @author ZhaoWeinan
 * @date 2018/10/28
 * @description
 */
public class BloomFileter {

 //使用加法hash算法，所以定义了一个8个元素的质数html" target="_blank">数组
 private static final int[] primes = new int[]{2, 3, 5, 7, 11, 13, 17, 19};
 //用八个不同的质数，相当于构建8个不同算法
 private Hash[] hashList = new Hash[primes.length];
 //创建一个长度为10亿的比特位
 private BitSet bits = new BitSet(256 << 22);

 public BloomFileter() {
 for (int i = 0; i < primes.length; i++) {
  //使用8个质数，创建八种算法
  hashList[i] = new Hash(primes[i]);
 }
 }

 //添加元素
 public void add(String value) {
 for (Hash f : hashList) {
  //算出8个信息指纹，对应到2的32次方个比特位上
  bits.set(f.hash(value), true);
 }
 }

 //判断是否在布隆过滤器中
 public boolean contains(String value) {
 if (value == null) {
  return false;
 }
 boolean ret = true;
 for (Hash f : hashList) {
  //查看8个比特位上的值
  ret = ret && bits.get(f.hash(value));
 }
 return ret;
 }

 //加法hash算法
 public static class Hash {

 private int prime;

 public Hash(int prime) {
  this.prime = prime;
 }

 public int hash(String key) {
  int hash, i;
  for (hash = key.length(), i = 0; i < key.length(); i++) {
  hash += key.charAt(i);
  }
  return (hash % prime);
 }
 }

 public static void main(String[] args) {

 BloomFileter bloomFileter = new BloomFileter();
 System.out.println(bloomFileter.contains("5324512515"));
 bloomFileter.add("5324512515");

 //维护1亿个在线用户
 for (int i = 1 ; i < 100000000 ; i ++){
  bloomFileter.add(String.valueOf(i));
 }

 long begin = System.currentTimeMillis();
 System.out.println(begin);
 System.out.println(bloomFileter.contains("5324512515"));
 long end = System.currentTimeMillis();
 System.out.println(end);
 System.out.println("判断5324512515是否在线使用了:" + (begin - end));
 }
}

这段代码是构建了一个10亿位的bitSet，然后把一亿个userId加入到了我们的布隆过滤器中，最近判断5324512515这个userId是否登录，打出代码的执行时间

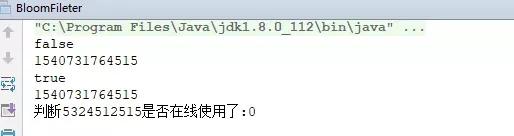
维护了1亿个userId以后检索5324512515是否登录，代码执行时间很短

在让我们来看看内存占用的情况

jvm整个的内存情况

再来看看BloomFileter这个类的实例，就占用了100多MB

实例的大小

看来布隆过滤器对于储存的效率确实很高

布隆过滤器的误识别问题

布隆过滤器的好处在于快速、省空间，但是有一定的误识别率，这个概率很小，要计算出现误识别的概率并不难，下面贴一段书上的话

假定布隆过滤器有m比特，里面有n个元素，每个元素对应k个信息指纹的hash函数，在这个布隆过滤器插入一个元素，那么比特位被设置成1的概率为1/m，它依然为0的概率为1-1/m，那么k个哈希函数都没有把他设置成1的概率为1-1/m的k次方，一个比特在插入了n个元素后，被设置为1的概率为1减1-1/m的kn次方，最后书上给出了一个公式，在这里就不贴了，就贴一个表吧，是m/n比值不同，以及K分别为不同的值得情况下的假阳性概率：

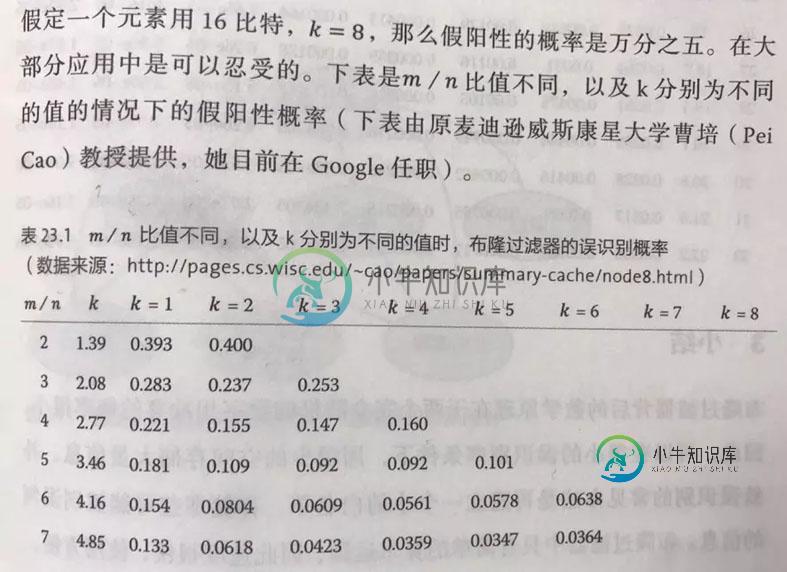
书上的表，直接拍下来的

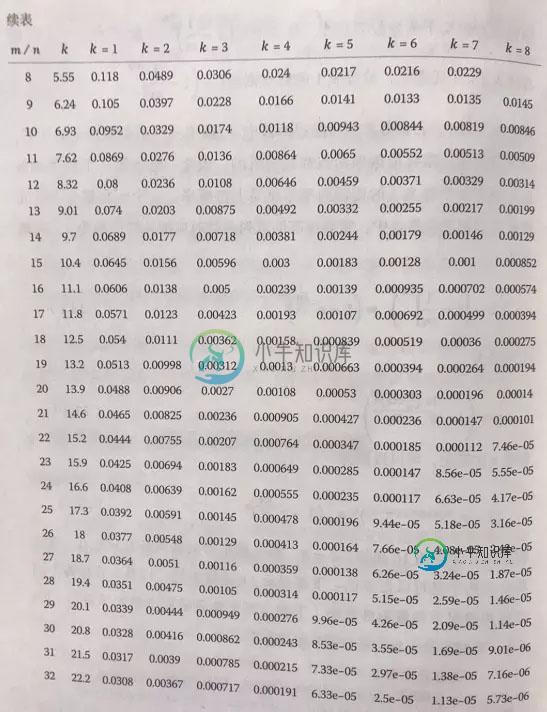
书上的表，直接拍下来的

布隆过滤器就为大家说到这里，欢迎大家来交流，指出文中一些说错的地方，让我加深认识。

总结

以上就是这篇文章的全部内容了，希望本文的内容对大家的学习或者工作具有一定的参考学习价值，如果有疑问大家可以留言交流，谢谢大家对小牛知识库的支持。