Python实现堆排序的方法详解
本文实例讲述了Python实现堆排序的方法。分享给大家供大家参考,具体如下:
堆排序作是基本排序方法的一种,类似于合并排序而不像插入排序,它的运行时间为O(nlogn),像插入排序而不像合并排序,它是一种原地排序算法,除了输入数组以外只占用常数个元素空间。
堆(定义):(二叉)堆数据结构是一个数组对象,可以视为一棵完全二叉树。如果根结点的值大于(小于)其它所有结点,并且它的左右子树也满足这样的性质,那么这个堆就是大(小)根堆。
我们假设某个堆由数组A表示,A[1]为树的根,给定某个结点的下标i,其父结点、左孩子、右孩子的下标都可以计算出来:
PARENT(i):
return i/2
LEFT(i):
return 2i
RIGHT(i):
return 2i+1
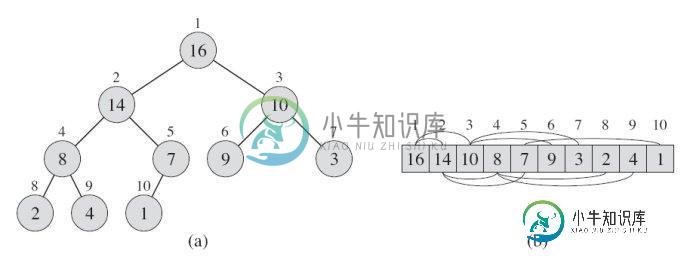
堆排序Python实现
所谓堆排序的过程,就是把一些无序的对象,逐步建立起一个堆的过程。
下面是用Python实现的堆排序的代码:
def build_max_heap(to_build_list):
"""建立一个堆"""
# 自底向上建堆
for i in range(len(to_build_list)/2 - 1, -1, -1):
max_heap(to_build_list, len(to_build_list), i)
def max_heap(to_adjust_list, heap_size, index):
"""调整列表中的元素以保证以index为根的堆是一个最大堆"""
# 将当前结点与其左右子节点比较,将较大的结点与当前结点交换,然后递归地调整子树
left_child = 2 * index + 1
right_child = left_child + 1
if left_child < heap_size and to_adjust_list[left_child] > to_adjust_list[index]:
largest = left_child
else:
largest = index
if right_child < heap_size and to_adjust_list[right_child] > to_adjust_list[largest]:
largest = right_child
if largest != index:
to_adjust_list[index], to_adjust_list[largest] = \
to_adjust_list[largest], to_adjust_list[index]
max_heap(to_adjust_list, heap_size, largest)
def heap_sort(to_sort_list):
"""堆排序"""
# 先将列表调整为堆
build_max_heap(to_sort_list)
heap_size = len(to_sort_list)
# 调整后列表的第一个元素就是这个列表中最大的元素,将其与最后一个元素交换,然后将剩余的列表再调整为最大堆
for i in range(len(to_sort_list) - 1, 0, -1):
to_sort_list[i], to_sort_list[0] = to_sort_list[0], to_sort_list[i]
heap_size -= 1
max_heap(to_sort_list, heap_size, 0)
if __name__ == '__main__':
to_sort_list = [4, 1, 3, 2, 16, 9, 10, 14, 8, 7]
heap_sort(to_sort_list)
print to_sort_list
更多关于Python相关内容可查看本站专题:《Python正则表达式用法总结》、《Python数据结构与算法教程》、《Python Socket编程技巧总结》、《Python函数使用技巧总结》、《Python字符串操作技巧汇总》、《Python入门与进阶经典教程》及《Python文件与目录操作技巧汇总》
希望本文所述对大家Python程序设计有所帮助。
-
本文向大家介绍C++堆排序算法的实现方法,包括了C++堆排序算法的实现方法的使用技巧和注意事项,需要的朋友参考一下 本文实例讲述了C++实现堆排序算法的方法,相信对于大家学习数据结构与算法会起到一定的帮助作用。具体内容如下: 首先,由于堆排序算法说起来比较长,所以在这里单独讲一下。堆排序是一种树形选择排序方法,它的特点是:在排序过程中,将L[n]看成是一棵完全二叉树的顺序存储结构,利用完全二叉
-
本文向大家介绍Python实现的堆排序算法示例,包括了Python实现的堆排序算法示例的使用技巧和注意事项,需要的朋友参考一下 本文实例讲述了Python实现的堆排序算法。分享给大家供大家参考,具体如下: 堆排序的思想: 堆是一种数据结构,可以将堆看作一棵完全二叉树,这棵二叉树满足,任何一个非叶节点的值都不大于(或不小于)其左右孩子节点的值。 将一个无序序列调整为一个堆,就可以找出这个序列的最大值
-
本文向大家介绍Python自定义sorted排序实现方法详解,包括了Python自定义sorted排序实现方法详解的使用技巧和注意事项,需要的朋友参考一下 题目 输入一个正整数数组,把数组里面的所有属猪拼接起来成为一个数打印能拼接起来的所有数字中最大/最小的那个。 思考 直观想法就是求出这个数组中所有数字的全排列,然后拼接起来,再比较大小即可,当然复杂度过高。 另一个想法,我们可以定义一个排序规则
-
本文向大家介绍PHP实现排序堆排序(Heap Sort)算法,包括了PHP实现排序堆排序(Heap Sort)算法的使用技巧和注意事项,需要的朋友参考一下 算法引进: 在这里我直接引用《大话数据结构》里面的开头: 在前面讲到 简单选择排序 ,它在待排序的 n 个记录中选择一个最小的记录需要比较 n - 1 次,本来这也可以理解,查找第一个数据需要比较这么多次是正常的,否则如何知道他是最小的记录。
-
本文向大家介绍Javascript堆排序算法详解,包括了Javascript堆排序算法详解的使用技巧和注意事项,需要的朋友参考一下 堆排序分为两个过程: 1.建堆。 堆实质上是完全二叉树,必须满足:树中任一非叶子结点的关键字均不大于(或不小于)其左右孩子(若存在)结点的关键字。 堆分为:大根堆和小根堆,升序排序采用大根堆,降序排序采用小根堆。 如果是大根堆,则通过调整函数将值最大的节点调整至堆根。
-
本文向大家介绍Python实现的堆排序算法原理与用法实例分析,包括了Python实现的堆排序算法原理与用法实例分析的使用技巧和注意事项,需要的朋友参考一下 本文实例讲述了Python实现的堆排序算法。分享给大家供大家参考,具体如下: 堆排序(Heapsort)是指利用堆这种数据结构所设计的一种排序算法。堆是一个近似完全二叉树的结构,并同时满足堆性质:即子结点的键值或索引总是小于(或者大于)它的父节

