javascript - 空间计算，求一个边长问题？

Question

求一个数学问题��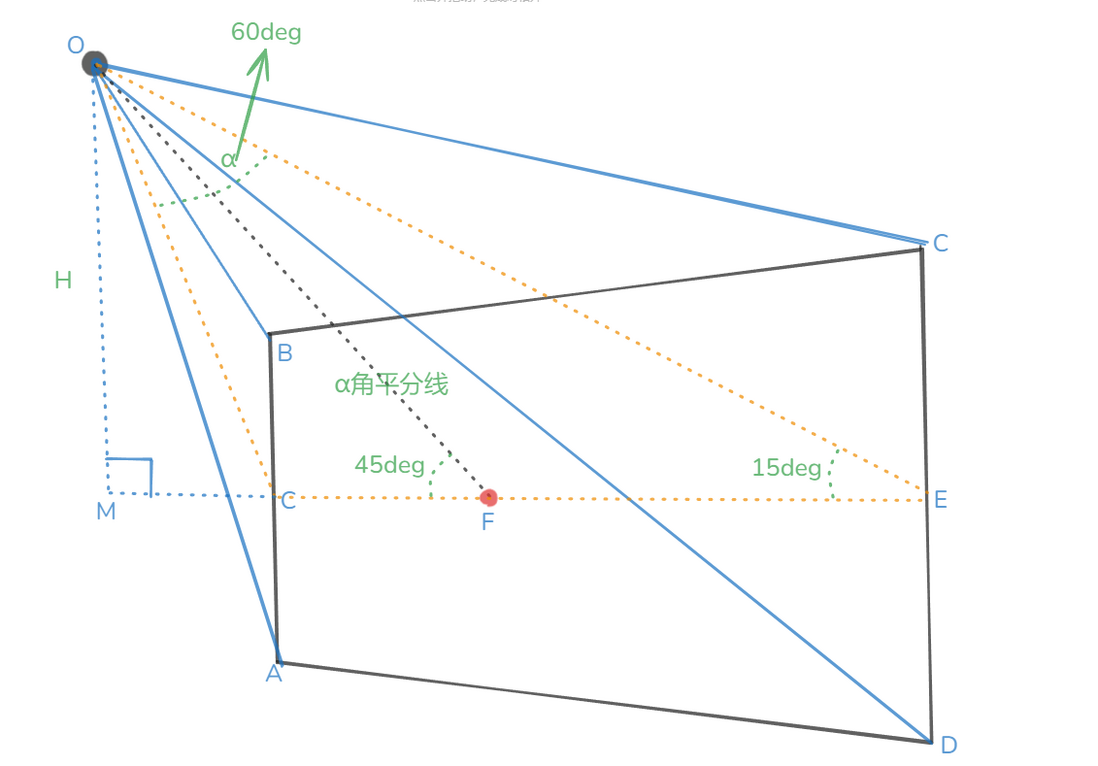

已知或者能够计算出来的相关条件：
1.ABCD是梯形，F是梯形内一点（不是中心点）
2.OC、OE、OF、CF、FE、OM、MC的长度均已知
3.OC、OE的夹角α为60°,OF是α的角度平分线

求 AB、CD的长度

Answer 1

要解决这个问题，我们需要明确一点：仅通过给出的条件，我们无法直接计算出AB和CD的确切长度，因为梯形ABCD的形状和大小还受到其他未知因素的影响（如梯形的高、角度等）。然而，我们可以利用已知条件尝试建立一些关系式或不等式，或者在某些特定假设下求解。

但考虑到问题的直接性，我们可以利用向量或几何关系来尝试表达AB和CD与已知条件的关系。不过，由于AB和CD是梯形的上底和下底，它们之间通常没有直接的数学关系（除非梯形是等腰梯形或其他特殊梯形），除非我们引入额外的条件（如梯形的高、角度等）。

假设与思路

1. 假设梯形的高已知（或可通过其他方式计算）：如果我们知道梯形的高（记为h），那么可以利用梯形面积与三角形面积的关系来建立方程。
2. 利用向量：在二维平面上，我们可以将OC、OE、OF等表示为向量，并利用向量的点积、叉积等性质来尝试找出AB和CD与已知向量的关系。但这种方法通常复杂且需要额外的几何或代数知识。
3. 利用角度和边长关系：由于OF是α的角度平分线，我们可以利用这一性质来找出与OC、OE相关的其他角度或边长关系。然而，这仍然不足以直接求出AB和CD。

结论

由于问题中给出的条件不足以直接求解AB和CD的长度，我们需要更多的信息（如梯形的高、角度等）来建立完整的数学模型。

Python代码示例（假设性）

如果我们假设梯形的高h可以通过某种方式计算出来（这里仅作为示例，实际上h的求解需要额外条件），我们可以尝试使用梯形和三角形的面积关系来建立方程。但请注意，以下代码是假设性的，并不直接解决当前问题：

import math

# 假设条件
h = 10  # 梯形的高，这里仅为示例
OC = 5
OE = 6
OF = 4
alpha = math.radians(60)  # 角度转换为弧度

# 梯形面积的计算通常需要上底和下底，但这里我们仅展示如何使用已知条件
# 实际上，我们需要额外的信息来求解AB和CD

# 示例：如果知道梯形面积A_trapezoid，可以尝试建立方程
# 假设梯形面积已知为A_trapezoid
A_trapezoid = 30

# 假设AB + CD是某个已知值或可以通过其他方式计算（这里仅为示例）
AB_plus_CD = 10

# 由于没有足够的信息，这里无法直接求解AB和CD
# 但可以展示如何使用已知条件来尝试建立方程
# 例如，如果我们知道梯形面积和AB+CD，可以建立关于AB和CD的方程
# 但这通常需要更多的条件或假设

# 注意：以下代码仅为示例，并不直接解决问题
# 假设AB = x, CD = y
# A_trapezoid = (x + y) * h / 2
# x + y = AB_plus_CD
# 但由于我们不知道AB_plus_CD的确切值，这里无法进一步求解

print("由于信息不足，无法直接求解AB和CD的长度。")

在实际应用中，我们需要根据具体问题的条件和要求来选择合适的数学方法和工具进行求解。