python3.x - 类抛物线求极值问题？

Question

以下是我这么做的原因，真正的问题在分隔线下面

最终目的是求空间中三个点在某个面上的投影匹配某个三角形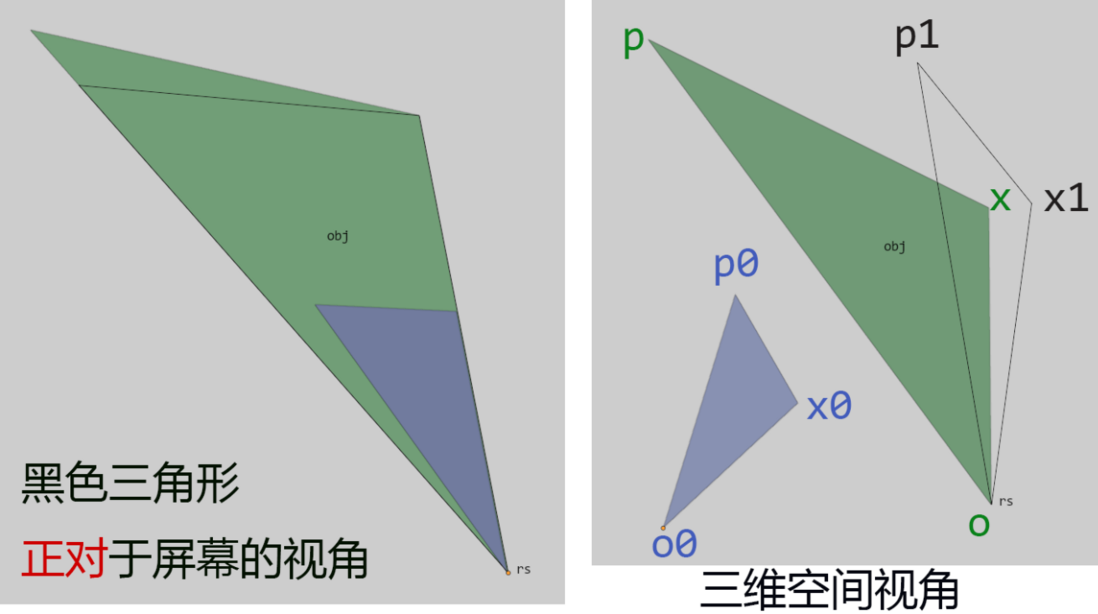

左边的紫色三角形只是为了让大家理解它的形状，实际是不会贴合到绿色三角形上的

也就是求黑色的这个面的法向，用来设置摄像机视角的
黑色的三角形是最终位置，辅助理解的，本质上是由紫色三角形变换得到的(它们形状一致，大小不一定一样)

所有已知信息都在图中。

我自己得出的解法是重叠o0与o(作为原点)，匹配ox，p到黑色三角形的投影座标与p1的距离最短。

---

以下是真正的问题

我编写了一个方法 xxx, 得到的结果是 p 的投影座标(p垂直投影到黑色三角形所在面)与p1的距离

# 放大紫色三角形，使o0_x0的长度 == o_x的长度，# 这是最大的情况，因为x的投影与o的距离不可能大于ox的长度scale_factor = (x - o).length / (x0 - o0).lengthd_o = xxx(o0, x0, p0)# 取一半尺寸d_m = xxx(...)d1 = 0.0sf_0 = 0sf_1 = 0if d_m > d_o:    d1 = d_m    sf_0 = scale_factor * 0.5    sf_1 = scale_factor    for i in range(20):        # 半分法更改尺寸，取得最小值        sf = (sf_1 + sf_0) / 2        d = xxx(...)        if d < d1:            d1 = d            sf_0 = sf        else:            sf_1 = sf            breakelse:    d1 = d_o    sf_0 = 0    sf_1 = scale_factor * 0.5    for i in range(20):        # 半分法更改尺寸，取得最小值        sf = (sf_1 + sf_0) / 2        d = xxx(...)        if d < d1:            d1 = d            sf_1 = sf        else:            sf_0 = sf            break

结果:
sf_0 < 最小的比例因子 < sf_1

这应该可以算作求抛物线的最低点问题，但我做不出抛物线方程，目前得到的结果还算可以，我想问有更好的方案吗？

谢谢！

Answer 1

这是一个关于几何投影和优化的复杂问题。根据您给出的信息，您已经有了基于半分法的解决方案，并希望寻找可能的优化方案。以下是一些建议：

1. 简化问题: 考虑到您所处理的是投影和几何变换的问题，首先尝试简化问题。例如，如果可能的话，尝试将问题分解为更小的部分，例如单独处理投影或变换的部分，然后逐步组合这些部分。
2. 使用数学库: 有许多现成的数学库可以帮助处理这种类型的问题。例如，SciPy 和 NumPy 在处理这种数值优化问题时非常有用。您可能想要查看这些库中的优化和插值函数，看看它们是否能够简化或加速您的代码。
3. 检查计算精度: 由于这是一个几何问题，计算精度可能会影响结果。确保您的计算考虑了所有必要的舍入误差和数值稳定性问题。
4. 并行化: 如果您的代码运行缓慢，考虑使用并行化来加速计算。例如，您可以使用 Python 的 multiprocessing 库或其他并行处理工具来同时处理多个任务。
5. 测试和验证: 在实施任何优化之前，先测试您的代码以确保它正确地实现了所需的功能。一旦您对代码的工作原理有了信心，就可以开始考虑优化。
6. 利用几何性质: 由于这是一个几何问题，您可能会发现一些有趣的几何性质可以用来简化计算或提高效率。例如，如果两个三角形在空间中是相似的，那么它们的变换可能会有一些有趣的性质。
7. 算法选择: 您已经使用了半分法来找到正确的比例因子。这是有效的，但不是最高效的方法。如果需要更快的解决方案，您可能需要研究其他算法或技术，如梯度下降法或牛顿法等优化算法。
8. 反馈和迭代: 最后，持续测试和反馈您的解决方案是非常重要的。每次修改代码后，都要重新运行测试并检查结果，以便了解您的更改是否有所改进。

请注意，对于具体的代码实现和数学公式，由于没有具体的编程语言和库的要求，我无法提供具体的代码示例。希望这些建议能帮到您！