r - 自学用R语言写了GARCH(1,1)的极大似然参数估计，十分需要帮我看看哪有问题?

Question

我必须在不使用R包(package)的情况下进行garch拟合过程，并估计参数。
我觉得是for循环那块有问题，但也想了好久不知道如何改善代码，请大家赐教，非常感谢！或者问问有没有自己编写的AR-GARCH程序可让我参考学习的
下面两个代码R都输出结果为：
Maximum Likelihood estimation
Newton-Raphson maximisation, 0 iterations
Return code 100: Initial value out of range.

顺便还有两个问题我想问问：
1、进行极大似然估计时，程序输出下面这句话是什么意思，对参数估计结果有影响吗
Return code 8: successive function values within relative tolerance limit (reltol)
2、如果估计时出现There were 50 or more warnings (use warnings() to see the first 50)，但是最终也会输出参数估计结果，而且参数的值也没啥问题，这些警告信息要处理吗，有影响吗
1: In sqrt(ht) : NaNs produced
2: In log(ht) : NaNs produced
3: In sqrt(ht) : NaNs produced
......
这是建模过程：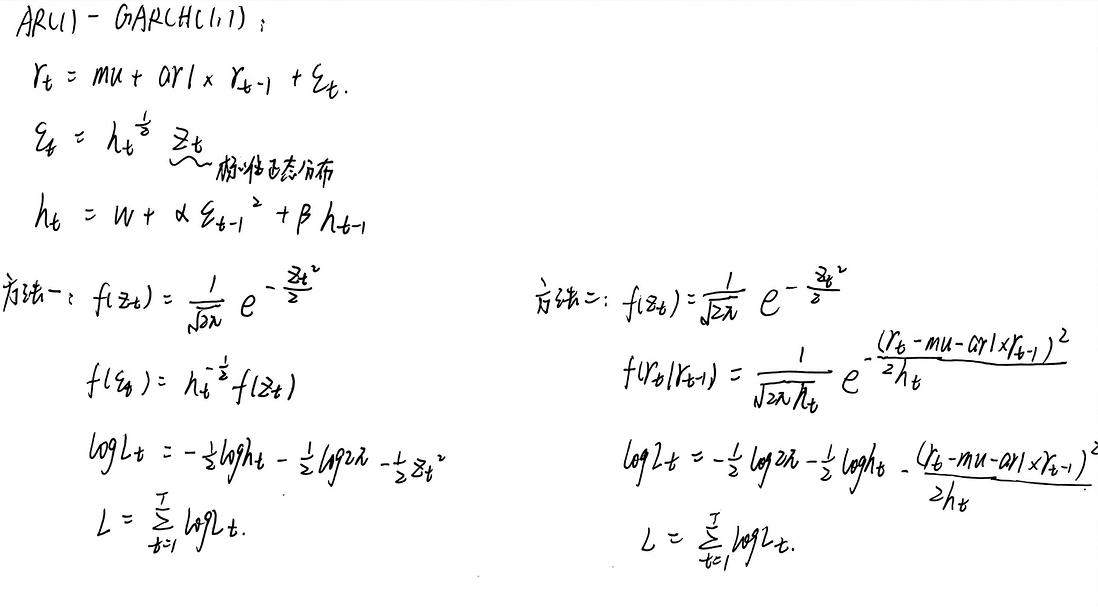

方法一：

lf8 <- function(pa){  mu <- pa[1]  ar1 <- pa[2]  omega <- pa[3]  alpha <- pa[4]  beta <- pa[5]  epsilon <- 0  ht <- ht_0  zt <- 0  l <- 0  for(i in 3: length(rt)){    epsilon[i] <- rt[i] - mu -ar1*rt[i-1]    ht[i] <- omega + alpha * (rt[i-1]-mu-ar1*rt[i-2])^2 + beta * ht[i-1]    zt[i] <- epsilon[i] / sqrt(ht[i])    l[i] <- -0.5*log(2*pi) - 0.5*log(ht[i]) - 0.5*(zt[i])^2  }  log_sum <- sum(l)  result <- l  return(result)}#对极大似然函数进行估计est8 <- maxLik(lf8, start=c(0, 0.2, 0.2, 0, 0.8))est8

方法二：

lf4 <- function(pa){  mu <- pa[1]  ar1 <- pa[2]  omega <- pa[3]  alpha <- pa[4]  beta <- pa[5]  ht <- ht_0  l <- 0  for(i in 3: length(rt)){    ht[i] <- omega + alpha * (rt[i-1]-mu-ar1*rt[i-2])^2 + beta * ht[i-1]    l[i] <- -0.5*log(2*pi) - 0.5*log(ht[i]) - 0.5*(rt[i] -mu -ar1*rt[i-1])^2 / ht[i]  }  log_sum <- sum(l)  result <- l  return(result)}#对极大似然函数进行估计est4 <- maxLik(lf4, start=c(0, 0.2, 0.2, 0, 0.8))est4

Answer 1

lf8 <- function(pa){  mu <- pa[1]  ar1 <- pa[2]  omega <- pa[3]  alpha <- pa[4]  beta <- pa[5]  epsilon <- numeric(length(rt))  ht <- ht_0  zt <- numeric(length(rt))  l <- numeric(length(rt))  for(i in 3: length(rt)){    epsilon[i] <- rt[i] - mu - ar1*rt[i-1]    ht[i] <- omega + alpha * (rt[i-1] - mu - ar1*rt[i-2])^2 + beta * ht[i-1]    zt[i] <- epsilon[i] / sqrt(ht[i])    l[i] <- -0.5 * log(2 * pi) - 0.5 * log(ht[i]) - 0.5 * zt[i]^2  }  log_sum <- sum(l)  return(-log_sum) # return the negative sum of likelihood}est8 <- maxLik(lf8, start=c(0, 0.2, 0.2, 0, 0.8))est8