如何在无向图中利用BFS进行循环检测中处理两个顶点之间的平行边？

Question

我是编程和学习算法的新手，当我读到BFS可以用于周期检测时，我正在研究BFS。我试图在一个具有邻接表表示的无向图G上实现同样的方法。我所做的如下：

•使用队列执行简单的BFS遍历，同时维护队列中排队节点的父节点。

•如果我遇到一个节点U，它有一个邻居V，这样V已经被访问，但是V不是U的父节点，那么这意味着图中存在循环。

#adjList is the adjacency list given as a dictionary
#myQueue is a double-sided queue containing node and its parent node ([Node, parNode])
#visited is a html" target="_blank">set containing visited nodes

while(myQueue):
    currNode, parNode = myQueue.pop() #dequeue operation
    visited.add(currNode) #Marking currNode as visited
    for childNode in adjList[currNode]: #Traversing through all children of currNode
        if currNode not in visited:
            myQueue.appendleft([childNode, currNode]) #Enqueue operation
        else:
            if childNode!=parNode: #Main logic for cycle detection
                print('CYCLE DETECTED')
                break

上面的方法是有效的，除非在两个顶点之间有超过1条边，例如，在下面的例子中，我们在顶点之间有2条边0和1:

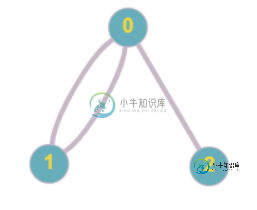
上图的邻接列表为:adjlist={0:[1,1,2],1:[0,0],2:[0]}。在这里，我们可以清楚地看到该图包含一个循环（在邻接表表示中，1在0的邻接表中出现两次，0在1的邻接表中出现两次，0的邻接表中出现两次），但是上述算法不能检测到相同的情况，因为当BFS到达顶点1时，顶点0已经被访问，但是顶点0也是顶点1的父节点，所以这个循环将不会被检测到。

我的问题是我如何修改上述算法来检测这种情况？

编辑：我也在有向图上尝试了同样的逻辑，我面临着类似的问题，即当我有一个从顶点0到顶点1的有向边和另一个从顶点1到顶点0的有向边时

Answer 1

我在堆栈交换的计算机科学论坛上得到了我问题的答案。这是答案的链接，我从那里复制了@Simon Weber发布的同样的答案

如果case到达您看到的节点的case已经被访问，但它是当前节点的父节点，您只需检查它们之间是否存在双边边。如何做到这一点取决于您的数据结构，但如果您的邻接列表是排序的，这将只是相当于搜索边缘，并检查它在那里的频率。

我看到的另一个问题是，您的邻接列表实际上并不包含任何边缘加倍的信息。