基于拓扑排序的有向无环依赖图并发处理分组任务

Question

我有一个任务类，它在执行前依赖于其他任务。我想将可以并行化的任务分组并排序。我决定它可以首先表示为DAG，并尝试使用JGrapht。首先，我遍历任务的输入列表，以获取所有具有依赖关系的任务，并将它们收集在一个列表中。然后，对于每个任务，我在图中创建一个顶点。

DirectedAcyclicGraph<Task, DefaultEdge> d = new DirectedAcyclicGraph<>(DefaultEdge.class);
Set<Task> all = collectAllTasks(tasks);
all.forEach(d::addVertex);

然后使用相同的列表，我试图创建节点之间的边。

all.forEach(task -> {
        Set<TaskName> predecessors = task.getPredecessors();

        predecessors.forEach(name -> {
            Task predecessor = taskService.getTaskByName(name);
            d.addEdge(predecessor, task);
        });

    });

然后我试着把任务分组

private Set<Set<TaskId>> groupTasks(DirectedAcyclicGraph<TaskId, DefaultEdge> dag) {
    Set<Set<TaskId>> groups = new LinkedHashSet<>();
    Iterator<TaskId> iterator = new TopologicalOrderIterator<>(dag);

    iterator.forEachRemaining(taskId -> {
        //source?
        if (dag.incomingEdgesOf(taskId).isEmpty()) {
            if (groups.isEmpty()) {
                Set<TaskId> set = new HashSet<>();
                set.add(taskId);
                groups.add(set);
            } else {
                groups.iterator().next().add(taskId);
            }
        }

        Set<TaskId> tasks = new HashSet<>(Graphs.successorListOf(dag, taskId));

        //sink?
        if (tasks.isEmpty()) {
            return;
        }

        groups.add(featuresGroup);
    });

    return groups;
}

因此，结果是有序和分组的任务，例如图

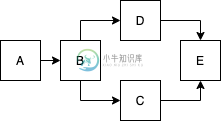
结果将是A， B，{C， D}， E.

然而，当B也是E的前身时，它就完全打破了这个例子

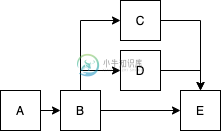
对于像上一个这样的图，如何实现A，B，{C，D}，E？有没有什么特别的算法我可以看看，或者我如何能以更好的方式实现这一点？谢谢

Answer 1

可使用以下程序获得溶液：

1. 第一组包含所有没有传入弧的任务：这些任务没有传入依赖项

使用JGraphT：

public static List<List<String>> getGroups(Graph<String, DefaultEdge> taskGraph){
    List<List<String>> groups = new ArrayList<>();
    //The first group contains all vertices without incoming arcs
    List<String> group = new LinkedList<>();
    for(String task : taskGraph.vertexSet())
        if(taskGraph.inDegreeOf(task) == 0)
            group.add(task);
    //Next we construct all remaining groups. The group k+1 consists of al vertices without incoming arcs if we were
    //to remove all vertices in the previous group k from the graph.
    do {
        groups.add(group);
        List<String> nextGroup = new LinkedList<>();
        for (String task : group) {
            for (String nextTask : Graphs.neighborSetOf(taskGraph, task)) {
                if (taskGraph.inDegreeOf(nextTask) == 1)
                    nextGroup.add(nextTask);
            }
            taskGraph.removeVertex(task); //Removes a vertex and all its edges from the graph
        }
        group=nextGroup;
    }while(!group.isEmpty());
    return groups;
}
public static Graph<String, DefaultEdge> getGraph1(){
    Graph<String, DefaultEdge> taskGraph=new SimpleDirectedGraph<>(DefaultEdge.class);
    Graphs.addAllVertices(taskGraph, Arrays.asList("A","B","C","D","E"));
    taskGraph.addEdge("A","B");
    taskGraph.addEdge("B","C");
    taskGraph.addEdge("B","D");
    taskGraph.addEdge("C","E");
    taskGraph.addEdge("D","E");
    return taskGraph;
}
public static Graph<String, DefaultEdge> getGraph2(){
    Graph<String, DefaultEdge> taskGraph=new SimpleDirectedGraph<>(DefaultEdge.class);
    Graphs.addAllVertices(taskGraph, Arrays.asList("A","B","C","D","E"));
    taskGraph.addEdge("A","B");
    taskGraph.addEdge("B","C");
    taskGraph.addEdge("B","D");
    taskGraph.addEdge("B","E");
    taskGraph.addEdge("C","E");
    taskGraph.addEdge("D","E");
    return taskGraph;
}
public static void main(String[] args){
    System.out.println("Graph1: "+getGroups(getGraph1()));
    System.out.println("Graph2: "+getGroups(getGraph2()));
}

输出：

Graph1: [[A], [B], [C, D], [E]]
Graph2: [[A], [B], [C, D], [E]]

注意：上面的代码假设输入图确实是一个有效的任务图。您可以构建一个额外的检查来识别循环依赖关系，例如，如果您有这样一个序列： A-