带加权边的1/0背包变分

Question

我目前正在研究一个路由问题（找到一个我想去的地方的子集[每个地方有一定的分数]，同时不超过最大的旅行时间），并提出了1/0背包问题的变体，似乎解决了我最初的问题。

根据维基百科，1/0背包被描述为：

给定一组物品，每个物品都有质量和价值，确定集合中每个物品的数量，以便总重量小于或等于给定的限制，总价值尽可能大。

因此，对于每个项目，都有一个固定的重量（质量），当试图解决问题时，可以很容易地使用它，例如使用动态规划。

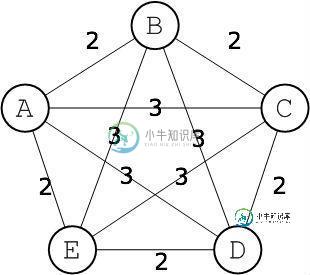
我对这个问题采取了完全错误的方法吗？你认为有更好的算法来解决这个问题吗？

Answer 1

首先，这个问题是NP难的。这里是从加权完全图中的最短哈密顿路到这一条的约简。给定一个图，我们可以将所有节点的值赋给1，然后对答案进行二分搜索。如果这个问题有一个多项式解，它可以判断是否有一条路径包含所有顶点，并且长度不超过给定值。这样，我们就可以在多项式时间内求解最短哈密顿路问题。在实践中，这意味着没有人知道你的问题的有效、正确的多项式解。

现在有两条路可走：

>

如果顶点数很少（大约20个），可以用动态规划得到精确解。状态为(mask,last_vertex)。该值是访问掩码中的所有顶点并停止在last_vertex中所需的最短时间。此解决方案的时间复杂度为O(2^n*n^2)。

如果顶点数大得多，就可以找到近似解。实现这一目标的方法有很多：启发式算法、不同的贪婪算法、随机抽样和局部优化等。