用递推方程求解程序的时间复杂度

Question

我想用递推方程找出程序的时间复杂度。那就是..

int f(int x)
{
if(x<1) return 1;
 else  return f(x-1)+g(x); 
}
int g(int x)
{
if(x<2) return 1;
 else return f(x-1)+g(x/2);
}

我写了它的递推方程，并试图解决它，但它继续变得复杂

T(n) =T(n-1)+g(n)+c
         =T(n-2)+g(n-1)+g(n)+c+c
         =T(n-3)+g(n-2)+g(n-1)+g(n)+c+c+c
         =T(n-4)+g(n-3)+g(n-2)+g(n-1)+g(n)+c+c+c+c
         ……………………….
        ……………………..
        Kth time …..
        =kc+g(n)+g(n-1)+g(n-3)+g(n-4).. .. . … +T(n-k)

Let at kth time input become 1
Then n-k=1
         K=n-1
Now i end up with this..
T(n)= (n-1)c+g(n)+g(n-1)+g(n-2)+g(n-3)+….. .. g(1)

我无法进一步解决它。无论如何，如果我们计算这个程序中函数调用的次数，就可以很容易地看出时间复杂度是指数的，但我想用递归来证明它。怎么能做到呢？

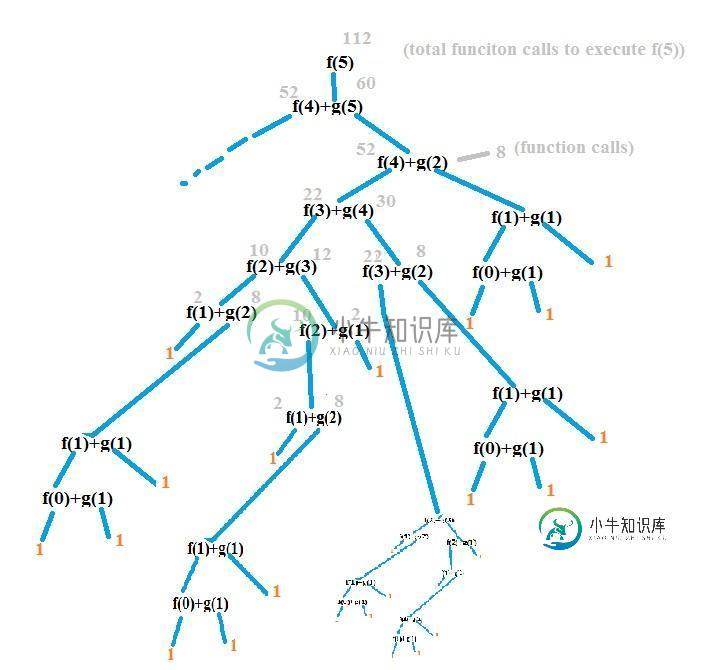
在Anwer 1的解释，看起来正确，类似的工作我做了。

这段代码中最困难的任务是编写它的递归方程。我画了另一张图，我确定了一些模式，我想我们可以从这张图中得到一些帮助，什么可能是递推方程。

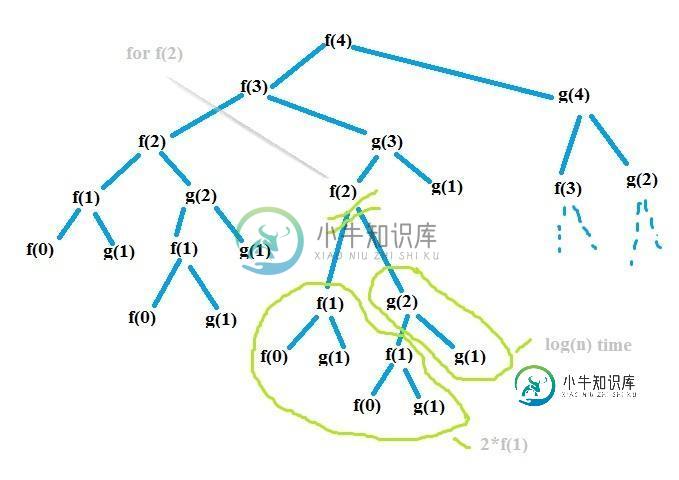
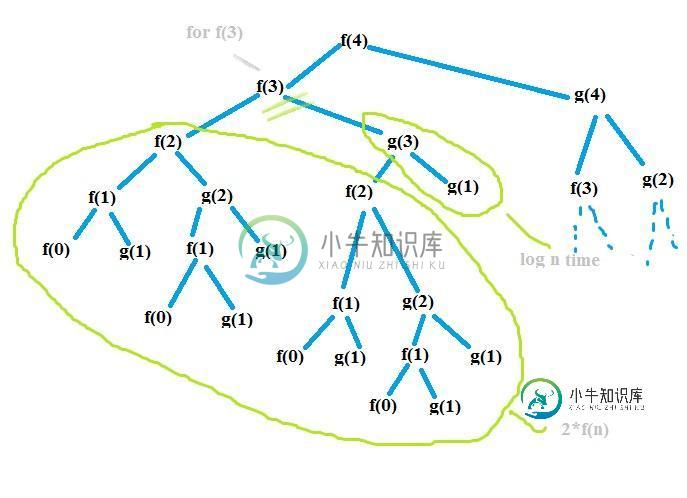
And I came up with this equation , not sure if it is right ??? Please help.

T(n) = 2*T(n-1) + c * logn

Answer 1

好的，我想我已经能够证明f(x)=Theta(2^x)（注意时间复杂度是相同的）。这也证明了g(x)=Theta(2^x)为f(x)>g(x)>f(x-1)。

首先，正如大家所指出的，很容易证明f(x)=Omega(2^x)。

现在我们有f(x)<=2f(x-1)+f(x/2)的关系（因为f(x)>g(x))

我们将说明，对于足够大的x，存在一些常量k>0，这样

f(x)<=k*H(x)，其中H(x)=(2+1/x)^x

这意味着f(x)=Theta(2^x)，就像h(x)=Theta(2^x)，这本身就来自于h(x)/2^x->sqrt(e)就像x->infinity（极限的wolfram alpha链接）。

现在（警告：较重的数学，perhap CS.StackExchange或math.StackExchange更适合）

根据wolfram alpha（点击链接，查看x=无穷大附近的级数展开），

h(x)=exp(x ln(2)+1/2+O(1/x))

因此，对于足够大的X（例如X>L)，我们有一个不等式

H(x)>=2H(x-1)+H(x/2)

现在有一些K（仅依赖于l（例如K=f(2l)))，这样

通过归纳，右边是

<=2*k*h(x)+k*h((x+1)/2)

我们之前证明了

2*H(x)+H((x+1)/2)<=H(x+1)

因此f(x+1)<=K*H(x+1)