Matplotlib xticks与直方图不对齐

Question

我正在使用 matplotlib 生成一些直方图，并且在弄清楚如何使直方图的 xtick 与条形对齐时遇到了一些麻烦。

这是我用来生成直方图的代码示例：

from matplotlib import pyplot as py

py.hist(histogram_data, 49, alpha=0.75)
py.title(column_name)
py.xticks(range(49))
py.show()

我知道historgram_data数组中的所有值都位于[0,1，…，48]。这意味着有49个独特的值。我想显示每个值的直方图。这是生成内容的图片。

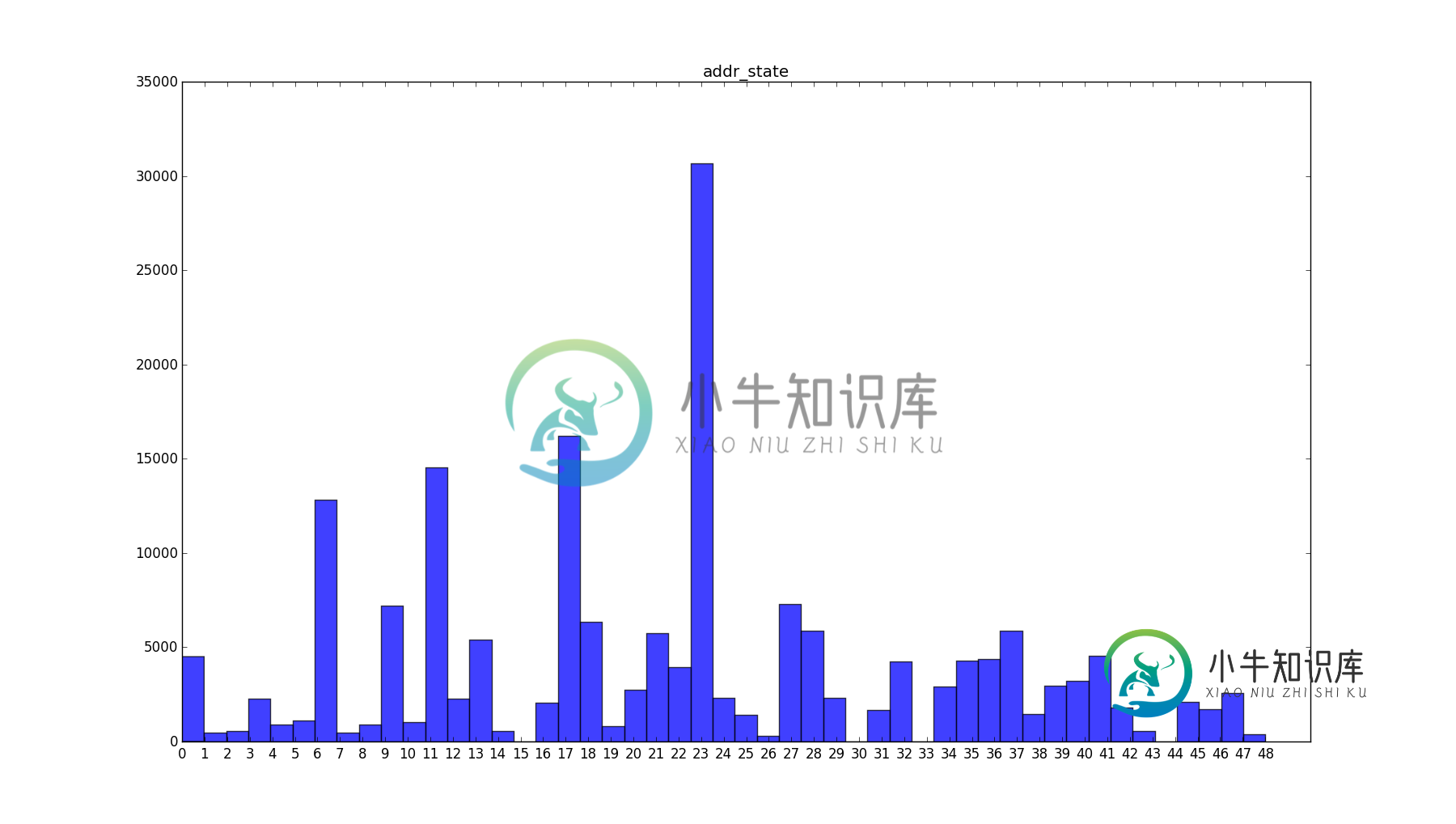
如何设置图形，使所有的x轴都与每个条形的左边、中间或右边对齐？

Answer 1

如果注释bins.append（排序（设置（标签））[-1]）：

bins = [i_bin - 0.5 for i_bin in set(labels)]
# bins.append(sorted(set(labels))[-1])
plt.hist(labels, bins)
plt.show()

如果没有：

bins = [i_bin - 0.5 for i_bin in set(labels)]
bins.append(sorted(set(labels))[-1])
plt.hist(labels, bins)
plt.show()

Answer 2

你要找的是知道每个箱子的边缘，并将其用作xtick。

假设您在x中有一些数字来生成直方图。

import matplotlib.pyplot as plt
import numpy as np
import random
n=1000
x=np.zeros(1000)
for i in range(n):
    x[i]=random.uniform(0,100)

现在让我们创建直方图。

n, bins, edges = plt.hist(x,bins=5,ec="red",alpha=0.7)

• n是具有编号的数组。每个bin中的项目
• bins是值位于bins边缘的数组
• 边缘是补丁对象的列表

现在，由于您有从左到右开始的垃圾箱边缘的位置，因此将其显示为xticks。

plt.xticks(bins)
plt.show()

Answer 3

简而言之：使用plt.hist（data， bins=range（50））来获取左对齐的bins，plt.hist（data， bins=np.arange（50）-0.5）来获取中心对齐的bins，等等。

此外，如果性能很重要，因为您需要唯一整数的计数，那么我将在最后显示几个稍微更有效的方法（np.bincount）。

作为您所看到的一个独立示例，请考虑以下内容：

import matplotlib.pyplot as plt
import numpy as np

# Generate a random array of integers between 0-9
# data.min() will be 0 and data.max() will be 9 (not 10)
data = np.random.randint(0, 10, 1000)

plt.hist(data, bins=10)
plt.xticks(range(10))
plt.show()

正如您所注意到的，垃圾箱没有与整数间隔对齐。这基本上是因为您要求0到9之间的10个垃圾箱，这与要求10个唯一值的垃圾箱不太一样。

您想要的箱数与唯一值的数量并不完全相同。在这种情况下，您实际应该做的是手动指定箱边缘。

为了解释发生了什么，让我们跳过矩阵图，只使用底层的 numpy.直方图函数。

例如，假设您有值[0，1，2，3]。你的第一直觉是：

In [1]: import numpy as np

In [2]: np.histogram([0, 1, 2, 3], bins=4)
Out[2]: (array([1, 1, 1, 1]), array([ 0.  ,  0.75,  1.5 ,  2.25,  3.  ]))

返回的第一个数组是计数，第二个数组是箱边（换句话说，其中条边将位于绘图中）。

注意，我们得到了预期的计数，但因为我们要求在数据的最小值和最大值之间有4个箱子，所以箱子边缘不在整数值上。

接下来，您可以尝试：

In [3]: np.histogram([0, 1, 2, 3], bins=3)
Out[3]: (array([1, 1, 2]), array([ 0.,  1.,  2.,  3.]))

请注意，bin边缘(第二个数组)是您所期望的，但计数不是。这是因为最后一个bin的行为与其他bin不同，如< code>numpy.histogram的文档中所述:

Notes
-----
All but the last (righthand-most) bin is half-open.  In other words, if
`bins` is::

  [1, 2, 3, 4]

then the first bin is ``[1, 2)`` (including 1, but excluding 2) and the
second ``[2, 3)``.  The last bin, however, is ``[3, 4]``, which *includes*
4.

因此，您实际应该做的是精确指定所需的bin边，或者在最后一个数据点之外包含一个bin边或将bin边移动到0.5间隔。例如：

In [4]: np.histogram([0, 1, 2, 3], bins=range(5))
Out[4]: (array([1, 1, 1, 1]), array([0, 1, 2, 3, 4]))

现在让我们将此应用于第一个示例，看看它是什么样子的：

import matplotlib.pyplot as plt
import numpy as np

# Generate a random array of integers between 0-9
# data.min() will be 0 and data.max() will be 9 (not 10)
data = np.random.randint(0, 10, 1000)

plt.hist(data, bins=range(11)) # <- The only difference
plt.xticks(range(10))
plt.show()

好的，太好了！但是，我们现在实际上有了左对齐的垃圾箱。如果我们想要中心对齐的垃圾箱来更好地反映这些是独特值的事实呢？

快速方法是只移动箱子边缘：

import matplotlib.pyplot as plt
import numpy as np

# Generate a random array of integers between 0-9
# data.min() will be 0 and data.max() will be 9 (not 10)
data = np.random.randint(0, 10, 1000)

bins = np.arange(11) - 0.5
plt.hist(data, bins)
plt.xticks(range(10))
plt.xlim([-1, 10])

plt.show()

同样，对于右对齐的箱子，只需按-1移位即可。

对于唯一整数值的特殊情况，我们可以采用另一种更有效的方法。

如果要处理以0开头的唯一整数计数，最好使用numpy。bincount比使用numpy.hist。

例如:

import matplotlib.pyplot as plt
import numpy as np

data = np.random.randint(0, 10, 1000)
counts = np.bincount(data)

# Switching to the OO-interface. You can do all of this with "plt" as well.
fig, ax = plt.subplots()
ax.bar(range(10), counts, width=1, align='center')
ax.set(xticks=range(10), xlim=[-1, 10])

plt.show()

这种方法有两大优点。一个是速度。数字直方图（因此也就是直方图）基本上通过数字数字化运行数据，然后通过数字数字来运行数据。由于您正在处理唯一的整数值，因此无需执行 numpy.digitale 步骤。

但是，更大的优势是对显示的更多控制。如果您更喜欢较细的矩形，只需使用较小的宽度：

import matplotlib.pyplot as plt
import numpy as np

data = np.random.randint(0, 10, 1000)
counts = np.bincount(data)

# Switching to the OO-interface. You can do all of this with "plt" as well.
fig, ax = plt.subplots()
ax.bar(range(10), counts, width=0.8, align='center')
ax.set(xticks=range(10), xlim=[-1, 10])

plt.show()