动态编程:我有重叠的子问题吗？

Question

让我们假设我有一个实数的 2D 数组。我从这个数组中的一个特定单元格开始，其中有一个特别大的数字。我想标记哪些其他单元格应该属于提到的起始单元格。规则是这样的：如果我找到从开始单元格走到另一个单元格的方法，则另一个单元格属于起始单元格。我只被允许在牢房上或下走动。我只被允许从数字较高的牢房走到数字较低的牢房。这是我从中心9开始的一个例子

我的伪算法是

function Step(cellNr):
    foreach neighborNr in neighbors_of(cellNr):
        if array_value(neighborNr) < array_value(cellNr):
            mark_cell(neighborNr)
            Step(neighborNr)
Step(centerNr)

现在来了第二个方面，我不仅为一个起始单元格执行此操作，而且为多个启动单元格执行此操作，例如

我研究了动态编程，发现需要满足两个条件才能应用动态编程:

• 子问题需要重叠
• 子问题需要有最优的子结构

“[动态规划]是指通过以递归方式将复杂问题分解为更简单的子问题来简化复杂问题[…]如果一个问题可以通过将其分解为子问题，然后递归地找到子问题的最优解来最优地解决，那么它就被称为具有最优子结构。[…]为了使动态规划适用，问题必须具有两个关键属性：最优子结构和重叠子问题。如果一个问题可以通过组合非重叠子问题的最优解来解决，则该策略称为“分而治之”。这就是为什么合并排序和快速排序不被归类为动态编程问题的原因。最优子结构是指给定优化问题的解可以通过组合其子问题的最优解来获得。这种最优子结构通常通过递归来描述。[…]重叠的子问题意味着子问题的空间必须很小，也就是说，任何解决问题的递归算法都应该反复解决相同的子问题，而不是生成新的子问题。”维基百科

我想知道我的算法是否是动态编程。它绝对是递归的，在子结构中似乎是最佳的。不过，我开始怀疑重叠的子结构。有一个斐波那契数的例子，但在我看来，关键方面是可以存储递归算法的中间结果。对于我的算法，无法存储中间结果 - 至少不能存储单个起始单元的一次运行。但是，当我考虑整个问题时，有许多启动单元，我们看到某些区域是连接的：

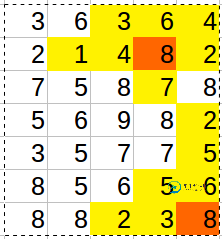
假设我们从左图中的橙色9开始，沿着绿色路径前进，直到到达蓝色5。从那里我们还可以到达蓝色3和蓝色2。我们完成了左橙色9的算法。

现在我们转到右图中较低的橙色 8。我们从这 8 开始，沿着绿色路径向上走到绿色 6。从那里我们到达蓝色 5。我们已经从之前的计算中知道（从左图中的橙色 9）蓝色 3 和蓝色 2 可以从蓝色 5 到达，因此我们可以一举标记它们，而无需重新计算路径。

这就是为什么我认为我的整体问题可以通过动态编程来解决。

< li >我的算法/问题是动态编程吗？为什么，为什么不？ < li >如果不能，我可以使它成为动态编程吗？如果可以，如何实现？

Answer 1

是的，这当然是一个动态规划问题。它实际上是最简单/最基本的动态规划问题——在有向无环图中找到从一个起始节点可以到达的所有节点（在您的情况下是多个起始节点）。您可以使用深度优先搜索或广度优先搜索来解决它。

它符合这样的定义：

最优结构？是的，我可以从一个单元格x到达的单元格是x加上我可以从x的较小的邻居到达的单元格的并集。

重叠子问题？是的，x的两个邻居都可以共享同一个较小的邻居。

为了使您发布的算法成为动态规划算法，您只需要记住如下子问题：

function Step(cellNr):
    foreach neighborNr in neighbors_of(cellNr):
        if array_value(neighborNr) < array_value(cellNr) AND cell_is_not_marked(neighborNr):
            mark_cell(neighborNr)
            Step(neighborNr)
Step(centerNr)

请注意，这也会将您的算法从指数时间更改为线性时间，并且它是深度优先搜索