大 2D 位矩阵中大小为 HxW 的最大子阵列

Question

我有一个大的NxN位数组，有K个1(其他都是0)。所有非零点的坐标都是已知的——换句话说，这个n×n数组可以表示为K对数组，每个数组包含一个非零点的x和y坐标。

给定一个HxW大小的子矩阵，我需要将其放在我的原始NxN数组上，使其覆盖大多数非零点。

输入：子矩阵的高度H和宽度W

输出：HxW子数组的x和y协弦，其内部有最多的协弦

之前也回答过类似的问题：2D矩阵中尺寸为HxW的最大子阵列，但在我的问题中更为复杂，因为N是巨大的，在我的例子中：N=60000，K

创建 60000x60000 数组将是一个内存消耗，即使它是一个位数组。这就是为什么我想出了用所有非零点表示该数组的想法：K 对的一维数组。

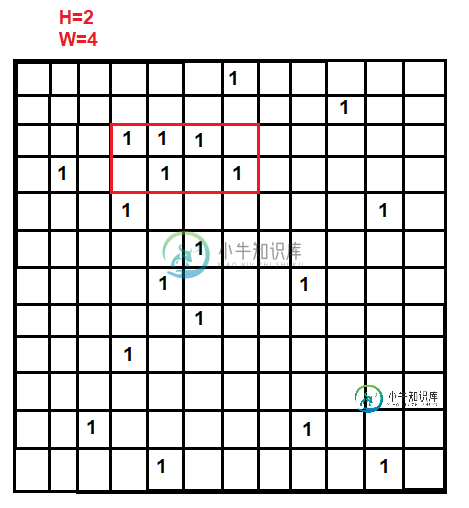
我能想到的一切都是内存和时间效率极低的，我正在寻找任何不会吃掉我所有公羊的解决方案。下面是它的外观：输出将是点 （4，3），因为从这一点开始的 HxW 子数组包含最多的子数组。

Answer 1

这里有一个算法，应该是O（k2*h）（它可能被优化为O（k*h*w）），并且对空间要求非常轻O（k）。它基于这样一个理论，即任何具有最高非零和的子矩阵必须在其左侧边缘有一个点（否则，在这个子矩阵的右侧可能有一个和更高的子矩阵）。因此，为了找到最高和，我们迭代每个非零点，并找到所有在其左侧边缘有该点的子矩阵，对子矩阵中每一行的当前点右侧W内的所有非零点求和。

下面是该算法的python实现。它首先创建每一行中的点的字典，然后如所述迭代每一点，存储该行右侧非零点的总和，然后基于该点计算每个子矩阵的总和。如果总和大于当前最大值，则存储该值及其位置。请注意，这使用了0索引列表，因此对于示例数据，最大值为（2，3）。

from collections import defaultdict

def max_subarray(n, nzp, h, w):
    maxsum = 0
    maxloc = (0, 0)
    # create a dictionary of points in a row
    nzpd = defaultdict(list)
    for p in nzp:
        nzpd[p[0]].append(p[1])
    # iterate over each of the non-zero points, looking at all
    # submatrixes that have the point on the left side
    for p in nzp:
        y, x = p
        pointsright = [0] * n
        for r in range(max(y-(h-1), 0), min(y+h, n)):
            # points within w to the right of this column on this row
            pointsright[r] = len([p for p in nzpd[r] if x <= p <= x+(w-1)])
        # compute the sums for each of the possible submatrixes
        for i in range(-h+1, h):
            thissum = sum(pointsright[max(y+i, 0):min(y+i+h, n)])
            if thissum > maxsum:
                maxsum = thissum
                maxloc = (y, x)
    # adjust the position in case the submatrix would extend beyond the last row/column
    maxloc = (min(n-h, maxloc[0]), min(n-w, maxloc[1]))
    # print the max sum
    print(f'{maxsum} found at location {maxloc}')

示例用法:

nzp = [(0, 6), (1, 9), (2, 3), (2, 4), (2, 5), 
       (3, 1), (3, 4), (3, 6), (4, 3), (4, 3), 
       (4, 10), (5, 5), (6, 4), (6, 8), (7, 5), 
       (8, 3), (10, 2), (10, 8), (11, 4), (11, 10)
       ]
  
max_subarray(12, nzp, 2, 4)

输出:

5 found at location (2, 3)

rexter上的演示