处理中如何手工将矩阵堆栈应用于坐标

Question

在处理过程中，当您应用矩阵变换时，您可以在画布上绘制，而不必担心x-y坐标的“真实”位置。

我认为按照同样的逻辑，我可以通过使用parentapplet.get(x，y，width,height）复制画布的一部分，它会自动移动x和y，但它不会，它使用坐标作为原始输入，而不对其应用矩阵堆栈。

因此，我认为处理这个问题的最简单方法是手动将矩阵堆栈应用于x、y、width和height值，并将结果用作get（）的输入。但是我找不到这样的函数，存在吗？

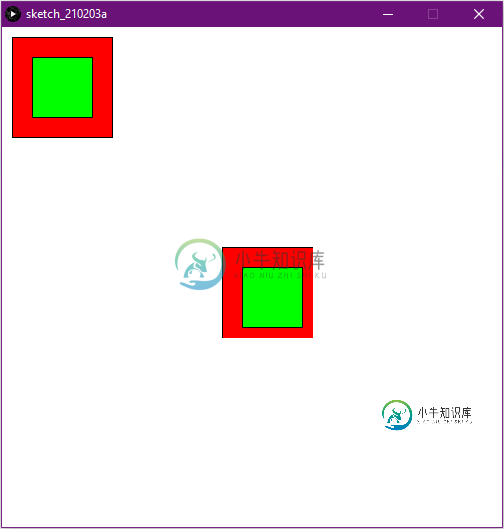
编辑：根据要求，这里有一个我的问题的例子

void settings(){
    size(500, 500);
}

void draw() {
  background(255);
  
  // Fancy rectangle for visibility
  fill(255, 0 ,0);
  rect(0, 0, 100, 100);
  fill(0, 255, 0);
  rect(20, 20, 60, 60);
  
  // copy rectangle and paste it elsewhere
  PImage img = get(0, 0, 101, 101);
  image(img, 200, 200);
}

void settings(){
    size(500, 500);
}

void draw() {
  background(255);
  pushMatrix();
  translate(10, 10);
  
  // Fancy rectangle for visibility
  fill(255, 0 ,0);
  rect(0, 0, 100, 100);
  fill(0, 255, 0);
  rect(20, 20, 60, 60);
  
  // copy rectangle and paste it elsewhere
  PImage img = get(0, 0, 101, 101);
  image(img, 200, 200);
  
  popMatrix();
}

Answer 1

你能提供更多的细节吗。可以使用pushMatrix（）/popmatrix（）来操纵坐标系，您还可以进一步手动将矩阵和向量相乘。

令人困惑的是，您调用了get(x,y,width,height)，但没有显示如何呈现pimage部分。很难猜出你提到的矩阵堆栈。你能发布一个示例片段吗？

如果以相同的x，y来呈现它，则调用get()，它应该以相同的x，y移位来呈现：

size(640, 360);
noFill();
strokeWeight(9);

PImage placeholderForPGraphics = loadImage("https://processing.org/examples/moonwalk.jpg");
image(placeholderForPGraphics, 0, 0);

int x = 420;
int y = 120;
int w = 32;
int h = 48;
// visualise region of interest
rect(x, y, w, h);

// grab the section sub PImage
PImage section = placeholderForPGraphics.get(x, y, w, h);

//filter the section to make it really standout
section.filter(THRESHOLD);
// display section at same location
image(section, x, y);

PMatrix m = g.getMatrix();
printArray(m.get(new float[]{}));

(g.printmatrix()应该更容易打印到控制台，但是如果需要操作实例，则需要调用getmatrix())

其中g是您的PGraphics实例。

然后您可以随意操作它：

m.translate(10, 20);
m.rotate(radians(30));
m.scale(1.5);

g.applyMatrix(m);

size(640, 360);
noFill();
strokeWeight(9);
// get the current transformation matrix
PMatrix m = g.getMatrix();
// print to console
println("before");
g.printMatrix();
// modify it
m.translate(160, 90);
m.scale(0.5);
// apply it
g.applyMatrix(m);
// print applied matrix
println("after");
g.printMatrix();


PImage placeholderForPGraphics = loadImage("https://processing.org/examples/moonwalk.jpg");
image(placeholderForPGraphics, 0, 0);

int x = 420;
int y = 120;
int w = 32;
int h = 48;
// visualise region of interest
rect(x, y, w, h);

// grab the section sub PImage
PImage section = placeholderForPGraphics.get(x, y, w, h);

//filter the section to make it really standout
section.filter(THRESHOLD);
// display section at same location
image(section, x, y);

void setup(){
  size(360, 360);
  
  // draw something manipulating the coordinate system
  PGraphics pg = createGraphics(360, 360);
  pg.beginDraw();
  pg.background(0);
  pg.noFill();
  pg.stroke(255, 128);
  pg.strokeWeight(4.5);
  pg.rectMode(CENTER);
  pg.translate(180,180);
  for(int i = 0 ; i < 72; i++){
    pg.rotate(radians(5));
    pg.scale(0.95);
    //pg.rect(0, 0, 320, 320, 32, 32, 32, 32);
    polygon(6, 180, pg);
  }
  pg.endDraw();
  
  // render PGraphics
  image(pg, 0, 0);
  
  }

void setup(){
  size(360, 360);
  
  // draw something manipulating the coordinate system
  PGraphics pg = createGraphics(360, 360);
  pg.beginDraw();
  pg.background(0);
  pg.noFill();
  pg.stroke(255, 128);
  pg.strokeWeight(4.5);
  pg.rectMode(CENTER);
  pg.translate(180,180);
  for(int i = 0 ; i < 72; i++){
    pg.rotate(radians(5));
    pg.scale(0.95);
    //pg.rect(0, 0, 320, 320, 32, 32, 32, 32);
    polygon(6, 180, pg);
  }
  pg.endDraw();
  
  // render PGraphics
  image(pg, 0, 0);

 
  // take a section of PGraphics instance
  int w = 180;
  int h = 180;
  int x = (pg.width - w) / 2;
  int y = (pg.height - h) / 2;
  PImage section = pg.get(x, y, w, h);
  
  // filter section to emphasise
  section.filter(INVERT);
  
  // render section at sampled location
  image(section, x, y);
  popMatrix();
  
}

void polygon(int sides, float radius, PGraphics pg){
  float angleIncrement = TWO_PI / sides;
  pg.beginShape();
  for(int i = 0 ; i <= sides; i++){
    float angle = (angleIncrement * i) + HALF_PI;
    pg.vertex(cos(angle) * radius, sin(angle) * radius);
  }
  pg.endShape();
}

下面是最后一个迭代，在一个独立的坐标空间中重新应用最后一个转换矩阵（使用push/pop矩阵调用）：

void setup(){
  size(360, 360);
  
  // draw something manipulating the coordinate system
  PGraphics pg = createGraphics(360, 360);
  pg.beginDraw();
  pg.background(0);
  pg.noFill();
  pg.stroke(255, 128);
  pg.strokeWeight(4.5);
  pg.rectMode(CENTER);
  pg.translate(180,180);
  for(int i = 0 ; i < 72; i++){
    pg.rotate(radians(5));
    pg.scale(0.95);
    //pg.rect(0, 0, 320, 320, 32, 32, 32, 32);
    polygon(6, 180, pg);
  }
  pg.endDraw();
  
  // render PGraphics
  image(pg, 0, 0);
  
  // take a section of PGraphics instance
  int w = 180;
  int h = 180;
  int x = (pg.width - w) / 2;
  int y = (pg.height - h) / 2;
  PImage section = pg.get(x, y, w, h);
  
  // filter section to emphasise
  section.filter(INVERT);
  
  // print last state of the transformation matrix
  pg.printMatrix();
  
  // get the last matrix state
  PMatrix m = pg.getMatrix();
  // isolate coordinate space
  pushMatrix();
  //apply last PGraphics matrix
  applyMatrix(m);
  // render section at sampled location
  image(section, x, y);
  popMatrix();
  
  save("state3.png");
}

void polygon(int sides, float radius, PGraphics pg){
  float angleIncrement = TWO_PI / sides;
  pg.beginShape();
  for(int i = 0 ; i <= sides; i++){
    float angle = (angleIncrement * i) + HALF_PI;
    pg.vertex(cos(angle) * radius, sin(angle) * radius);
  }
  pg.endShape();
}

这是一个极端的例子，因为0.95downscale应用了72次，因此呈现的图像非常小。还要注意旋转是递增的。

根据您的更新代码片段，似乎在pushmatrix()和get()之间存在混淆。

int sampleX = 10;
int sampleY = 10;

void settings(){
    size(500, 500);
}

void draw() {
  background(255);
  pushMatrix();
  translate(sampleX, sampleY);
  
  // Fancy rectangle for visibility
  fill(255, 0 ,0);
  rect(0, 0, 100, 100);
  fill(0, 255, 0);
  rect(20, 20, 60, 60);
  
  // copy rectangle and paste it elsewhere
  PImage img = get(sampleX, sampleY, 101, 101);
  image(img, 200, 200);
  
  popMatrix();
}

void settings(){
    size(500, 500);
}

void setup() {
  background(255);
  pushMatrix();
  translate(10, 10);
  // Fancy rectangle for visibility
  fill(255, 0 ,0);
  rect(0, 0, 100, 100);
  fill(0, 255, 0);
  rect(20, 20, 60, 60);
  // local to global coordinate conversion using PMatrix
  // g is the global PGraphics instance every PApplet (sketch) uses
  PMatrix m = g.getMatrix();
  printArray(m.get(null));
  // the point in local coordinate system
  PVector local = new PVector(0,0);
  // multiply local point by transformation matrix to get global point
  // we pass in null to get a new PVector instance: you can make this more efficient by allocating a single PVector ad re-using it instead of this basic demo
  PVector global = m.mult(local,null);
  // copy rectangle and paste it elsewhere
  println("local",local,"->global",global);
  PImage img = get((int)global.x, (int)global.y, 101, 101);
  image(img, 200, 200);
  
  popMatrix();
}

要根据变换矩阵计算向量的位置，只需将向量乘以该矩阵。非常粗略地说，Push/Pop矩阵会发生什么（每个Push/Pop堆栈使用一个转换矩阵，然后将其乘以全局坐标系）。（请注意效率/预先分配矩阵和向量的注释）。

就代码而言，这将更加冗长，如果您使用大量html" target="_blank">嵌套转换，则可能需要进行一些规划，但您可以更好地控制选择使用哪些转换。

一个更简单的解决方案是切换到P3DOpenGL呈现器，它允许您使用screenx()、screeny()进行转换。（也签出modelx()/modely())

void settings(){
    size(500, 500, P3D);
}

void draw() {
  background(255);
  pushMatrix();
  translate(10, 10);
  // Fancy rectangle for visibility
  fill(255, 0 ,0);
  rect(0, 0, 100, 100);
  fill(0, 255, 0);
  rect(20, 20, 60, 60);
  // local to global coordinate conversion using modelX,modelY
  float x = screenX(0, 0, 0);
  float y = screenY(0, 0, 0);
  println(x,y);
  PImage img = get((int)x, (int)y, 101, 101);
  image(img, 200, 200);
  
  popMatrix();
}

请记住，您想抓取一个简单地应用了翻译的矩形。由于get()不会考虑旋转/缩放，因此对于更复杂的情况，您可能不仅需要将左上角的坐标转换为全局坐标，还需要将右下角的坐标转换为具有偏移量的坐标。其思想是在转换后的框周围计算更大的边界框（没有旋转），这样当调用get()时，将返回整个感兴趣的区域（而不仅仅是一个剪裁的部分）。