在Python中用于条件密度估计的工具

Question

关闭。 此问题不符合堆栈溢出准则。它当前不接受答案。

想改善这个问题吗？ 更新问题，使其成为Stack Overflow的主题。

去年关闭。

改善这个问题

我有一个大数据集，每行包含3个属性：A，B，C

列A：可以采用值1、2和0。列B和C：可以采用任何值。

我想使用直方图对P（A = 2 | B，C）进行密度估计，并使用python绘制结果。

我不需要执行此操作的代码，我可以尝试自己解决这个问题。我只需要知道应该使用的程序和工具？

Answer 1

要回答您的总体问题，我们应该经过不同的步骤并回答不同的问题：

• 如何读取csv文件（或文本数据）？

• 如何过滤数据？

• 如何绘制数据？

在每个阶段，您都需要使用一些技术和特定的工具，在不同的阶段，您可能还会有不同的选择（您可以在互联网上寻找不同的选择）。

1-如何读取csv文件：

有一个内置的功能可以在存储数据的csv文件中进行浏览。但是大多数人建议熊猫处理csv文件。

后安装熊猫包，您可以使用阅读您的CSV文件Read_CSV命令。

import pandas as pd

df= pd.read_csv("file.csv")

由于您没有共享csv文件，因此我将随机创建一个数据集来说明即将执行的步骤。

import pandas as pd
import numpy as np

t= [1,1,1,2,0,1,1,0,0,2,1,1,2,0,0,0,0,1,1,1]
df = pd.DataFrame(np.random.randn(20, 2), columns=list('AC'))
df['B']=t  #put a random column with only 0,1,2 values, then insert it to the dataframe

注意：Numpy是一个python软件包。使用数学运算会很有帮助。您主要不需要它，但是我在这里提到它是为了消除混乱。

如果在这种情况下打印df，您将得到以下结果：

         A         C    B
0  -0.090162  0.035458  1
1   2.068328 -0.357626  1
2  -0.476045 -1.217848  1
3  -0.405150 -1.111787  2
4   0.502283  1.586743  0
5   1.822558 -0.398833  1
6   0.367663  0.305023  1
7   2.731756  0.563161  0
8   2.096459  1.323511  0
9   1.386778 -1.774599  2
10 -0.512147 -0.677339  1
11 -0.091165  0.587496  1
12 -0.264265  1.216617  2
13  1.731371 -0.906727  0
14  0.969974  1.305460  0
15 -0.795679 -0.707238  0
16  0.274473  1.842542  0
17  0.771794 -1.726273  1
18  0.126508 -0.206365  1
19  0.622025 -0.322115  1

2–如何过滤数据：有多种过滤数据的技术。最简单的方法是选择数据框内的列名+条件。在我们的情况下，条件是在B列中选择值“ 2”。

l= df[df['B']==2]
print l

您还可以使用其他方式，例如groupby，lambda遍历数据帧并应用不同的条件来过滤数据。

for key in df.groupby('B'):
    print key

如果运行上述脚本，您将获得：

对于第一个：仅B == 2的数据

           A         C  B
3  -0.405150 -1.111787  2
9   1.386778 -1.774599  2
12 -0.264265  1.216617  2

对于第二个：打印结果分为几组。

(0,            A         C  B
4   0.502283  1.586743  0
7   2.731756  0.563161  0
8   2.096459  1.323511  0
13  1.731371 -0.906727  0
14  0.969974  1.305460  0
15 -0.795679 -0.707238  0
16  0.274473  1.842542  0)
(1,            A         C  B
0  -0.090162  0.035458  1
1   2.068328 -0.357626  1
2  -0.476045 -1.217848  1
5   1.822558 -0.398833  1
6   0.367663  0.305023  1
10 -0.512147 -0.677339  1
11 -0.091165  0.587496  1
17  0.771794 -1.726273  1
18  0.126508 -0.206365  1
19  0.622025 -0.322115  1)
(2,            A         C  B
3  -0.405150 -1.111787  2
9   1.386778 -1.774599  2
12 -0.264265  1.216617  2)

• 如何绘制数据：

绘制数据的最简单方法是使用matplotlib

在B列中绘制数据的最简单方法是运行：

import random
import matplotlib.pyplot as plt

xbins=range(0,len(l))
plt.hist(df.B, bins=20, color='blue')
plt.show()

您将得到以下结果：

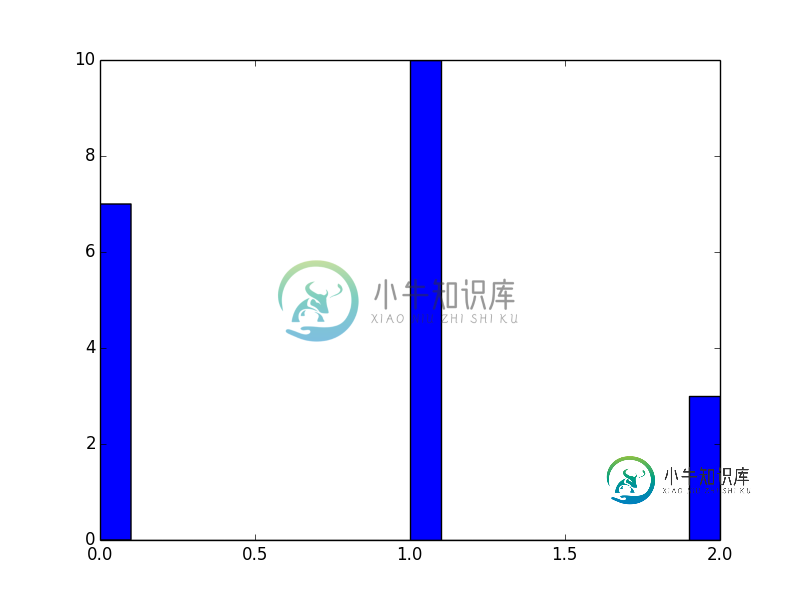
如果要组合绘制结果，则应使用不同的颜色/技术以使其有用。

import numpy as np
import matplotlib.pyplot as plt
a = df.A
b = df.B
c = df.C
t= range(20)
plt.plot(t, a, 'r--',  b, 'bs--', c, 'g^--')
plt.legend()
plt.show()

结果是：

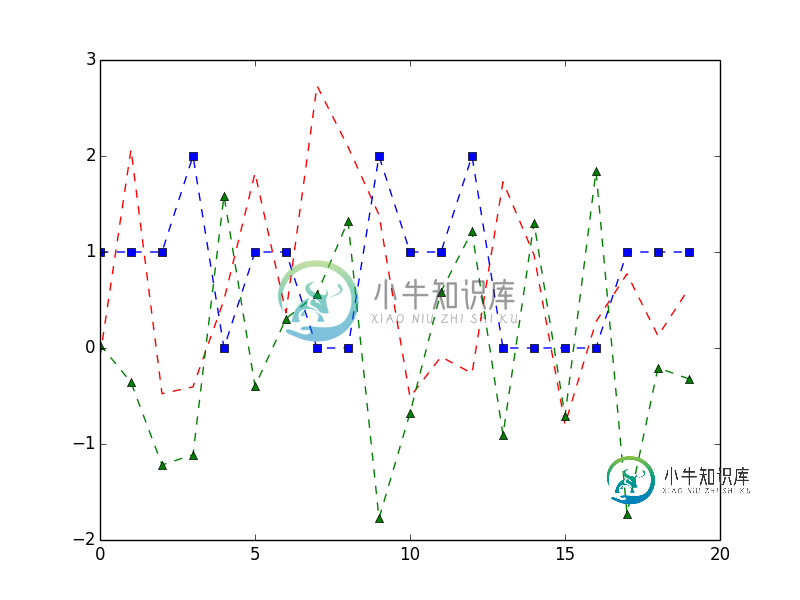
绘制数据是由特定需求决定的。您可以通过查看marplotlib.org官方网站的示例来探索绘制数据的不同方法。