完整推导svm一遍，还有强化学习说一说，dqn的各种trick了解多少，以及都怎么实现

Answer 1

参考回答：

SVM推导：

支持向量机是一种二分类模型，他的基本想法就是基于训练集和样本空间中找到一个最好的划分超平面，将两类样本分割开来，首先你就要知道什么样的划分发才能称为“最”好划分

看上图，二维平面上有两类样本，一类是用‘+’表示，另一类用‘-’表示，那么中间那几条划分线每条都能将两类样本分割开来，但我们我们一眼就注意到中间那条加粗的划分超平面，似乎他是最好的，因为两类的样本点都离他挺远的，专业点说就是该划分超平面对训练样本局部扰动的‘容忍’性最好。好，这还只是个二维平面，我们可以通过可视化大概寻找这样一个超平面，但如果三维，四维，五维呢，我们必须用我们擅长的数学去描述它，推导它。

在样本空间中，划分超平面可用表示，记为（w,b）,样本点（xi,yi）到划分超平面的函数间隔为 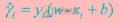，几何间隔为：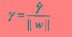

若，可知函数间隔和几何间隔相等，若超平面参数w，b成比例的改变（超平面没有变），则函数间隔也是成比例的改变，而几何间隔不变。

支持向量机的基本想法就是求解能够正确划分训练数据集并且几何间隔最大的分离超平面，表达为数学公式即为：

其实函数间隔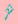的取值并不影响最优化问题的解，假设将w和b成倍的改变为aw，ab，那么函数间隔也会相应变成a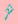，函数间隔的对上面最优化问题的不等式没有影响，也对目标函数没有影响，因此为简便，取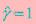，而且我们注意到最大化等价于最小化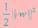（为啥取平方呢，因为后面好求导），便可得到下面支持线性可分（线性不可分的情况后面会提到）的支持向量机的最优化问题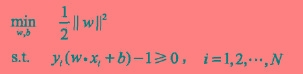这是一个凸二次优化的问题，可以直接求解，但是为了简便呢，我们要应用拉格朗日对偶性，求解他的对偶问题其实求解对偶问题相比于原问题有一下几点好处(1).对偶问题更容易求解，因为不用求w了 (2)我们可以自然引入核函数，这样可以推广到线性不可分分类问题上建立拉格朗日函数，引进拉格朗日乘子，定义拉格朗日函数：根据原始问题的对偶性，原始问题的对偶性是极大极小问题，即 首先我们来求最小，零L(w,b,a)分别对w和b求导为零可得将其代入对偶问题，可得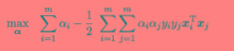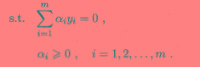解出alpha之后，那么w，b也相应得到啦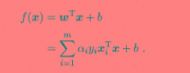接下来，我们看看很有意思的上式不等式约束的kkt条件（不懂请百度）带给我们的信息咦，对于任意训练样本，总有或者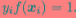，也就是说最终与模型有关的的样本点都位于最大间隔的边界上，我们称之为支持向量，其余的样本点与模型无关在前面的讨论中，我们都是聊的线性可分的情况，那么大多数情况下都线性不可分怎么办，比如这样（如左）山人自有妙计，我们可以将样本先映射到高维特征空间，然后就可以继续分割了（如右）前面我们说到了对偶问题是公式中涉及到计算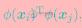，xi，xj是映射到特征空间之后的内积，由于特征维数可能会很高，甚至是无穷多维，直接计算很困难，所以我们引入了核函数：这样我们就可以不用麻烦的计算内积了 dqn的各种trick：第一个Trick。DQN引入卷积层。模型通过Atari游戏视频图像了解环境信息并学习策略。DQN需要理解接收图像，具有图像识别能力。卷积神经网络，利用可提取空间结构信息卷积层抽取特征。卷积层提取图像中重要目标特征传给后层做分类、回归。DQN用卷积层做强化学习训练，根据环境图像输出决策。第二个Trick。Experience Replay。深度学习需要大量样本，传统Q-Learning online update方法(逐一对新样本学习)不适合DQN。增大样本，多个epoch训练，图像反复利用。Experience Replay，储存Agent Experience样本，每次训练随机抽取部分样本供网络学习。稳定完成学习任务，避免短视只学习最新接触样本，综合反复利用过往大量样本学习。创建储存Experience缓存buffer，储存一定量较新样本。容量满了，用新样本替换最旧样本，保证大部分样本相近概率被抽到。不替换旧样本，训练过程被抽到概率永远比新样本高很多。每次需要训练样本，直接从buffer随机抽取一定量给DQN训练，保持样本高利用率，让模型学习到较新样本。第三个Trick。用第二个DQN网络辅助训练，target DQN，辅助计算目标Q值，提供学习目标公式里的maxaQ(st+1,a)。两个网络，一个制造学习目标，一个实际训练，让Q-Learning训练目标保持平稳。强化学习 Q-Learning学习目标每次变化，学习目标分部是模型本身输出，每次更新模型参数会导致学习目标变化，更新频繁幅度大，训练过程会非常不稳定、失控，DQN训练会陷入目标Q值与预测Q值反馈循环(陷入震荡发散，难收敛)。需要稳定target DQN辅助网络计算目标Q值。target DQN，低频率、缓慢学习，输出目标Q值波动较小，减小训练过程影响。第四个Trick。Double DQN。传统DQN高估Action Q值，高估不均匀，导致次优Action被高估超过最优Action。targetDQN 负责生成目标Q值，先产生Q(st+1,a)，再通过maxa选择最大Q值。Double DQN，在主DQN上通过最大Q值选择Action，再获取Action在target DQN Q值。主网选择Action，targetDQN生成Action Q值。被选择Q值，不一定总是最大，避免被高估次优Action总是超过最优Action，导致发现不了真正最好Action。学习目标公式：Target=rt+1+γ·Qtarget(st+1,argmaxa(Qmain(st+1,a)))。第五个Trick。Dueling DQN。Dueling DQN，Q值函数Q(st,at)拆分，一部分静态环境状态具有价值V(st)，Value；另一部分动态选择Action额外带来价值A(at)，Advantage。公式，Q(st,at)=V(st)+A(at)。网络分别计算环境Value和选择Action Advantage。Advantage，Action与其他Action比较，零均值。网络最后，不再直接输出Action数量Q值，输出一个Value，及Action数量 Advantage值。V值分别加到每个Advantage值上，得最后结果。让DQN学习目标更明确，如果当前期望价值主要由环境状态决定，Value值大，所有Advantage波动不大；如果期望价值主要由Action决定，Value值小，Advantage波动大。分解让学习目标更稳定、精确，DQN对环境状态估计能力更强。